Description
Bo has been in Changsha for four years. However he spends most of his time staying his small dormitory. One day he decides to get out of the dormitory and see the beautiful city. So he asks to Xi to know whether he can get to another bus station from a bus station. Xi is not a good man because he doesn’t tell Bo directly. He tells to Bo about some buses’ routes. Now Bo turns to you and he hopes you to tell him whether he can get to another bus station from a bus station directly according to the Xi’s information.
Input
The first line of the input contains a single integer T (0<T<30) which is the number of test cases. For each test case, the first contains two different numbers representing the starting station and the ending station that Bo asks. The second line is the number n (0<n<=50) of buses’ routes which Xi tells. For each of the following n lines, the first number m (2<=m<= 100) which stands for the number of bus station in the bus’ route. The remaining m numbers represents the m bus station. All of the bus stations are represented by a number, which is between 0 and 100.So you can think that there are only 100 bus stations in Changsha.
Output
For each test case, output the “Yes” if Bo can get to the ending station from the starting station by taking some of buses which Xi tells. Otherwise output “No”. One line per each case. Quotes should not be included.
Sample Input
3 0 3 3 3 1 2 3 3 4 5 6 3 1 5 6 0 4 2 3 0 2 3 2 2 4 3 2 1 4 2 1 0 3
Sample Output
No Yes Yes
复杂度分析
空间复杂度为O(N),建立一个集合的时间复杂度为O(1),N次合并M查找的时间复杂度为O(M Alpha(N)),这里Alpha是Ackerman函数的某个反函数,在很大的范围内(人类目前观测到的宇宙范围估算有10的80次方个原子,这小于前面所说的范围)这个函数的值可以看成是不大于4的,所以并查集的操作可以看作是线性的。
基本操作
并查集是一种非常简单的数据结构,它主要涉及两个基本操作,分别为:
A. 合并两个不相交集合
B. 判断两个元素是否属于同一个集合
(1) 合并两个不相交集合(Union(x,y))
合并操作很简单:先设置一个数组Father[x],表示x的“父亲”的编号。那么,合并两个不相交集合的方法就是,找到其中一个集合最父亲的父亲(也就是最久远的祖先),将另外一个集合的最久远的祖先的父亲指向它。

图为两个不相交集合,b图为合并后Father(b):=Father(g)
(2) 判断两个元素是否属于同一集合(Find_Set(x))
本操作可转换为寻找两个元素的最久远祖先是否相同。可以采用递归实现。
优化
(1) Find_Set(x)时,路径压缩
寻找祖先时,我们一般采用递归查找,但是当元素很多亦或是整棵树变为一条链时,每次Find_Set(x)都是O(n)的复杂度。为了避免这种情况,我们需对路径进行压缩,即当我们经过”递推”找到祖先节点后,”回溯”的时候顺便将它的子孙节点都直接指向祖先,这样以后再次Find_Set(x)时复杂度就变成O(1)了,如下图所示。可见,路径压缩方便了以后的查找。
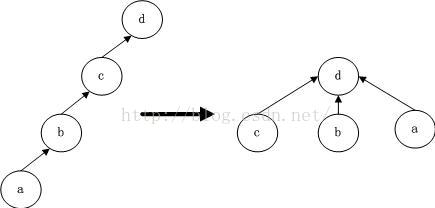

(2) Union(x,y)时,按秩合并
即合并的时候将元素少的集合合并到元素多的集合中,这样合并之后树的高度会相对较小。
应用
并查集常作为另一种复杂的数据结构或者算法的存储结构。常见的应用有:求无向图的连通分量个数,最近公共祖先(LCA),带限制的作业排序,实现Kruskar算法求最小生成树等
翻译

#include<stdio.h> #define N 105 int father[N]; int a[N]; void init(int m){ for(int i=0;i<m;i++) //初始化 father[i]=i; } int getfather(int x){ //获取根节点 while(x!=father[x]) x=father[x]; return x; }
/*
int getfather(int x) {
if(x != father[x])
father[x] = getfather(father[x]); // 路径压缩
return father[x];
} */
bool same(int x,int y){ //判断是否相同 return getfather(x)==getfather(y); } void unions(int x,int y){ //并集合 x=getfather(x); y=getfather(y); if(x!=y) father[x]=y; } int main(){ int T; scanf("%d",&T); while(T--){ init(100); int start,end,n; scanf("%d%d",&start,&end); scanf("%d",&n); while(n--){ int m; scanf("%d",&m); for(int i=0;i<m;i++) scanf("%d",&a[i]); for(int i=1;i<m;i++) unions(a[i-1],a[i]); } printf("%s ",getfather(start)==getfather(end)?"Yes":"No"); } }