并查集

1. 并查集算法

2.朋友圈

 

 最近攻克自己不太熟悉的算法，例如最短路径，线段树，并查集等算法，顺手做个记录

1. 并查集算法

说玄乎其实挺玄乎的，说简单其实真的就是名字，并，查，集。所谓的查，就是查找一个用户的老大是谁，并，就是把两个人的老大合到一起，集就是集合。因此这个数据结构就是对集合进行查找和合并，追根结底，就是一个把老大合并的过程，这样我们集合就可以不断的合并。借用其他博客的一张图片（https://blog.csdn.net/qq_41593380/article/details/81146850）

我们可以看出，只要两个人认识，那么这些人就是一个集合，因此，我们通过并查集，不断地找某一个人的老大是谁，如果两个人老大是同一个人，那么他们就是一伙的；如果不是一伙的，那么他们俩要么打一架，要么就是找出他们的leader是谁，然后将两个不同的leader进行合并，因此，可以看出，他们是一个自下而上的树。 

从上面的思路可以看出，并查集本质上就是两个函数，一个查(find)，一个并(union)。

2. 并查集的实现

 以一道题为例

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

输入：
[[1,1,0],
[1,1,0],
[0,0,1]]
输出：2
解释：已知学生 0 和学生 1 互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回 2 。

（1）这道题经典并查集，那么我们首先定义我们的并查集。

list1 = [i for i in range(N)]

这个N即是学生的数量，list[i]代表第i个学生的leader是谁，我们这里可以认为，leader就是他们认识，我并不在乎A是B的leader还是B是A的leader。

（2）定义 查 的功能

def find(x):
    son= x
    while list1[x] != x:#查找老大
        x = list1[x] 
    while son != x: 
        list1[son],son = x,list1[son]#合并路径
    return x

从这里我们可以看出，我们的查很简单，只要一直查询到 list[x] == x，也就是x号就是自己的老大，说明已经到了根节点了，不然我就一直去查询老大是谁。第二个while循环是进行减枝，合并路径。我没有必要将树的深度加深，这样不利于查询。

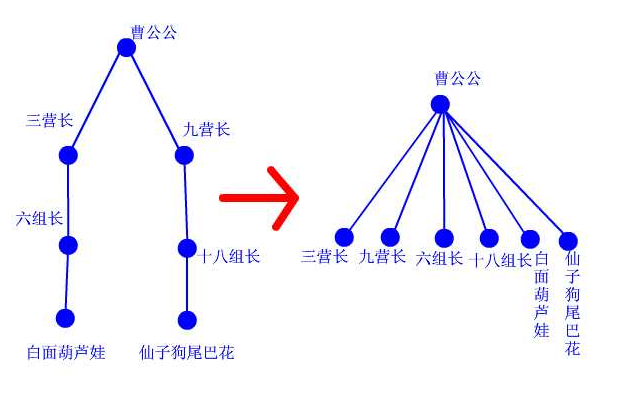
 （3）定义 并 操作

def union(x,y):
    xleader = find(x) #发现x的leader
    yleader = find(y) #发现y的leader
    if xleader != yleader:
        list1[yleader] = xleader #如果不相等，那么就将其中一个集合合并到另外一个集合中，本质上就是一个树的另外一个分支。

并的操作也是很简单的。通过合并leader，就完成了两个朋友圈的合并。

（4）解题

在有了这两个操作后，我们就可以对我们的题中的关系矩阵进行遍历，如果遇到认识的，就合并两个人，让其中一个人当leader。

for i in range(N):
     for k in range(i+1,N):
          if M[i][k] == 1:
              union(i,k)

我们需要注意的是就是这是一个对称矩阵，因此只要对i->n的人进行遍历就可以了。

在我们做完我们list的更改以后，我们只要再遍历一遍我们的人数，找出有多少个leader就可以了！

set1 = set()
for i in range(N):
      set1.add(find(i))

是的，我们只要返回我们的set的长度就可以了！这个我觉得是一个入门并查集的最好题目了，哈哈。

所有代码如下：

class Solution:
    def findCircleNum(self, M: List[List[int]]) -> int:
        N = len(M)
        list1 = [i for i in range(N)]
        def find(x):
            son= x
            while list1[x] != x:
                x = list1[x] #寻找leader
            while son != x:
                list1[son],son = x,list1[son]#剪枝
            return x
        def union(x,y):
            xleader = find(x)
            yleader = find(y)
            if xleader != yleader:
                list1[yleader] = xleader
        for i in range(N):
            for k in range(i+1,N):
                if M[i][k] == 1:
                    union(i,k)
        set1 = set()
        for i in range(N):
            set1.add(find(i))
        return len(set1)