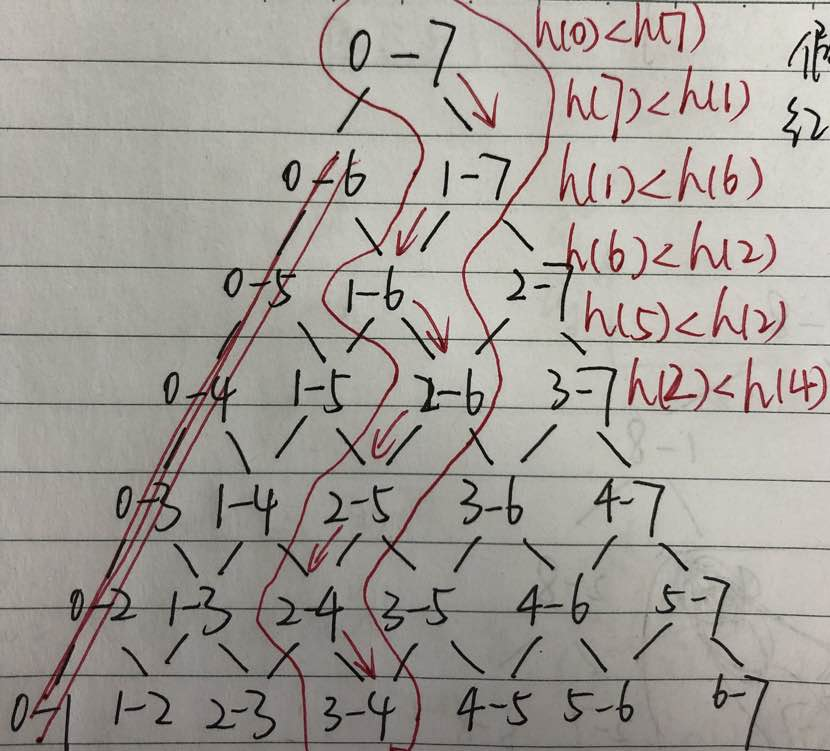leetcode 11题 水池最大容积
题目描述
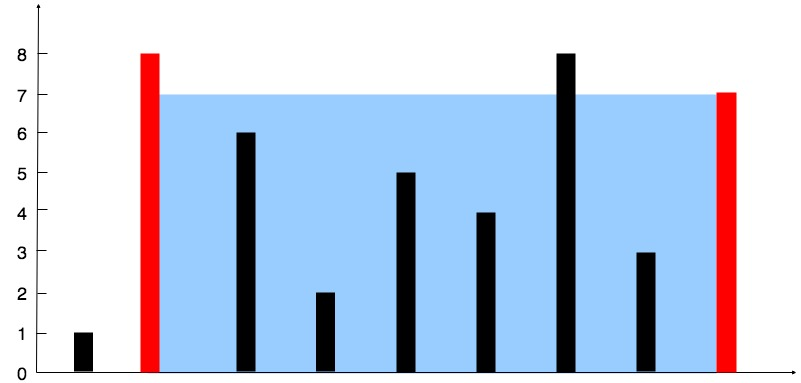
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
思路:
这是一道动态规划的问题,有两个思路,第一个思路是从左到右 寻找最大的水槽面积,其实就是新的标杆和最左标杆,最右标杆,原始面积三个面积的最大值,然后新标杆不断增长,最终得到最大的面积
第二个思路便是不断变小,也就是最左标杆和最右标杆,然后二者不断缩小最小值。
第一种思路:
def maxArea(height): left = 0 right = 1 count = 1 distance = right - left maxwater = min(height[left], height[right]) * distance while (count < len(height)-1): count += 1 nextright = count print(count) nextleftwater = min(height[left], height[nextright]) * (nextright - left) nextrightwater = min(height[right], height[nextright]) * (nextright - right) templist = [maxwater, nextleftwater, nextrightwater] if templist.index(max(templist)) == 0: continue if templist.index(max(templist)) == 1: right = nextright maxwater = nextleftwater else: left = right right = nextright maxwater = nextrightwater return maxwater
问题:
这种并不能通过所有的测试案例,问题就是在于如果之前增长是相同的,如果单纯不变,那么对于下一个面积的计算就会有问题,比如[1,2,4,3]就会出现问题,根本原因还是因为没有覆盖所有的转态空间,导致异常,但是想修改起来就非常麻烦。
第二种思路
使用双指针解法,也就是标准解法,使用不断缩小两条边,我们可以发现其实如果不断缩小的话,面积不会出现第一种思路的问题了。
class Solution: def maxArea(self, height: List[int]) -> int: left = 0 right = len(height)-1 maxwater = min(height[left],height[right])*(right-left) while(left < right): if height[left] < height[right]: left += 1 tempwater = min(height[left],height[right])*(right-left) if tempwater > maxwater: maxwater = tempwater else: right -= 1 tempwater = min(height[left],height[right])*(right-left) if tempwater > maxwater: maxwater = tempwater return maxwater
再解释一下为什么这样是对的。
首先,如果我们将左标杆加一,那么实际情况中面积很肯能会变小,应为距离缩短了,除非出现缩短了左边以后左标杆变长了,总体面积才会增加.
借用题解中一个人的非常好的思路(雫空)这个人的思路,非常感谢他的分享,讲的很透彻,
用h(i)表示第i条线段的高度,S(ij)表示第i条线段和第j条线段圈起来的面积。
可知 h(0) < h(7),从而S(07) = h(0) * 7。
有S(06) = min(h(0), h(6)) * 6。
当h(0) <= h(6),有S(06) = h(0) * 6;
当h(0) > h(6),有S(06) = h(6) * 6,S(06) < h(0) * 6。
由此可知,S(06)必然小于S(07)。