1.问题
什么是最短路算法
是实现图上最短路的算法,常见的有Dijkstra算法,Floyd算法。
2.解析
Dijkstra算法

如图红线这条路径可以被蓝线所优化,这就是松弛操作
Floyd算法

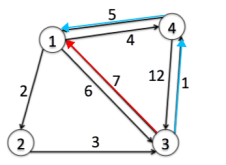

如图红线这些路径也可以被蓝线所优化。
3. 设计
Dijstra算法
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
- 从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
- 重复步骤(2)和(3),直到遍历完所有顶点。
Floyd算法
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
4.分析
Dijstra算法:nlogn
Floyd算法:n3
5. 源码
https://github.com/Tinkerllt/algorithm-work.git

1 //Floyd 2 #include<stdio.h> 3 #include<iostream> 4 #include<cmath> 5 #include<cstring> 6 #include<algorithm> 7 #include<bitset> 8 #include<set> 9 #include<deque> 10 #include<queue> 11 #include<vector> 12 //#include<unordered_map> 13 #include<map> 14 #include<stack> 15 using namespace std; 16 #define ll long long 17 #define ull unsigned long long 18 #define pii pair<int,int> 19 #define Pii pair<ll,ll> 20 #define m_p make_pair 21 #define l_b lower_bound 22 #define u_b upper_bound 23 const int inf=0x3f3f3f3f; 24 const ll linf=0x3f3f3f3f3f3f3f3f; 25 const int maxn=3e5+11; 26 const int maxm=2e3+11; 27 const int mod=1e9+7; 28 const double eps=1e-5; 29 ll rd(){ll x = 0, f = 1; char ch = getchar();while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f;} 30 inline ll qpow(ll a,ll b){ll res=1;while(b){if(b&1){res*=a;res%=mod;}b>>=1;a=a*a%mod;}return res;} 31 inline ll gcd(ll a,ll b){if(b==0) return a;return gcd(b,a%b);} 32 //iterator 33 //head 34 int mp[maxm][maxm];//邻接矩阵存图 35 int main(){ 36 int n=rd(),m=rd(); 37 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) {if(i==j) continue;mp[i][j]=inf;} 38 for(int i=1;i<=m;i++){ 39 int s=rd(),e=rd(),v=rd(); 40 mp[s][e]=v;//有向图 41 } 42 for(int k=1;k<=n;k++){ 43 for(int i=1;i<=n;i++){ 44 for(int j=1;j<=n;j++){ 45 mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);//松弛操作 46 } 47 } 48 } 49 for(int i=1;i<=n;i++){ 50 for(int j=1;j<=n;j++){ 51 if(i==j) continue; 52 printf("st-%d ed-%d:len-%d ",i,j,mp[i][j]==inf?-1:mp[i][j]); 53 } 54 } 55 } 56 /*4 8 57 1 2 2 58 2 3 3 59 1 3 6 60 3 1 7 61 1 4 4 62 4 1 5 63 4 3 12 64 3 4 1*/

1 //dijkstra 2 #include<stdio.h> 3 #include<iostream> 4 #include<cmath> 5 #include<cstring> 6 #include<algorithm> 7 #include<bitset> 8 #include<set> 9 #include<deque> 10 #include<queue> 11 #include<vector> 12 //#include<unordered_map> 13 #include<map> 14 #include<stack> 15 using namespace std; 16 #define ll long long 17 #define ull unsigned long long 18 #define pii pair<int,int> 19 #define Pii pair<ll,ll> 20 #define m_p make_pair 21 #define l_b lower_bound 22 #define u_b upper_bound 23 const int inf=0x3f3f3f3f; 24 const ll linf=0x3f3f3f3f3f3f3f3f; 25 const int maxn=3e5+11; 26 const int maxm=2e3+11; 27 const int mod=1e9+7; 28 const double eps=1e-5; 29 ll rd(){ll x = 0, f = 1; char ch = getchar();while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f;} 30 inline ll qpow(ll a,ll b){ll res=1;while(b){if(b&1){res*=a;res%=mod;}b>>=1;a=a*a%mod;}return res;} 31 inline ll gcd(ll a,ll b){if(b==0) return a;return gcd(b,a%b);} 32 //iterator 33 //head 34 priority_queue<pii>q;//从大到小 35 int head[maxn],ver[maxn],Next[maxn],cnt,edge[maxn]; 36 int dis[maxn],vis[maxn],n,m; 37 void addedge(int x,int y,int v){//链式前向星存边 38 Next[++cnt]=head[x]; 39 head[x]=cnt; 40 ver[cnt]=y; 41 edge[cnt]=v; 42 } 43 void dijkstra(int st){//单元最短路的源这里是1 44 memset(dis,inf,sizeof dis); 45 dis[st]=0; 46 vis[st]=1; 47 q.push(m_p(0,st)); 48 while(!q.empty()) { 49 int x=q.top().second; 50 q.pop(); 51 for(int i=head[x];i;i=Next[i]){ 52 int y=ver[i],z=edge[i]; 53 if(vis[y]) continue; 54 if(dis[y]>dis[x]+z){ 55 dis[y]=dis[x]+z; 56 q.push(m_p(-dis[y],y)); 57 vis[y]=1; 58 } 59 } 60 } 61 for(int i=2;i<=n;i++) printf("1->%d:%d ",i,dis[i]); 62 } 63 int main(){ 64 n=rd(),m=rd(); 65 for(int i=1;i<=m;i++){ 66 int x=rd(),y=rd(),z=rd(); 67 addedge(x,y,z); 68 } 69 dijkstra(1); 70 } 71 /*8 11 72 1 2 1 73 3 1 2 74 2 4 2 75 4 3 1 76 5 4 2 77 4 6 8 78 6 5 2 79 5 7 2 80 7 6 3 81 8 6 2 82 7 8 3*/
