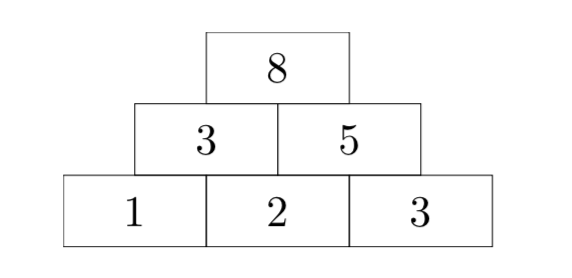
Do you like number pyramids? Given a number sequence that represents the base, you are usually supposed to build the rest of the "pyramid" bottom-up: For each pair of adjacent numbers, you would compute their sum and write it down above them. For example, given the base sequence [1, 2, 3][1,2,3], the sequence directly above it would be [3, 5][3,5], and the top of the pyramid would be [8][8]:
However, I am not interested in completing the pyramid – instead, I would much rather go underground. Thus, for a sequence of nn non-negative integers, I will write down a sequence of n + 1n+1 non-negative integers below it such that each number in the original sequence is the sum of the two numbers I put below it. However, there may be several possible sequences or perhaps even none at all satisfying this condition. So, could you please tell me how many sequences there are for me to choose from?
Input Format
The input consists of:
- one line with the integer nn (1 le n le 10^6)(1≤n≤106), the length of the base sequence.
- one line with n integers a_1, cdots , a_na1,⋯,an (0 le ai le 10^8(0≤ai≤108 for each i)i), forming the base sequence.
Output Format
Output a single integer, the number of non-negative integer sequences that would have the input sequence as the next level in a number pyramid.
样例输入1
6 12 5 7 7 8 4
样例输出1
2
样例输入2
3 10 1000 100
样例输出2
0
题目来源
German Collegiate Programming Contest 2018
#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <utility> #include <vector> #include <map> #include <queue> #include <stack> #include <cstdlib> #include <cmath> typedef long long ll; #define lowbit(x) (x&(-x)) #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 using namespace std; #define pi acos(-1) int n; const int N=1e6+9; const ll inf=1e14+4; ll a[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); } ll l=0,r=0; ll maxx=inf,minn=0;//一定要>=0 for(int i=1;i<=n;i++){ if(i%2==1){ l=a[i]-r; maxx=min(maxx,l); } if(i%2==0){ r=a[i]-l; minn=max(minn,r*(-1)); } } //解的范围[minn,maxx] /* 如 12 5 7 11 x 12-x -7+x 14-x x-3 令x==0 0 12 -7 14 -3 [7,12] */ if(minn>maxx){ printf("0 "); } else{ printf("%lld ",maxx-minn+1); } return 0; }