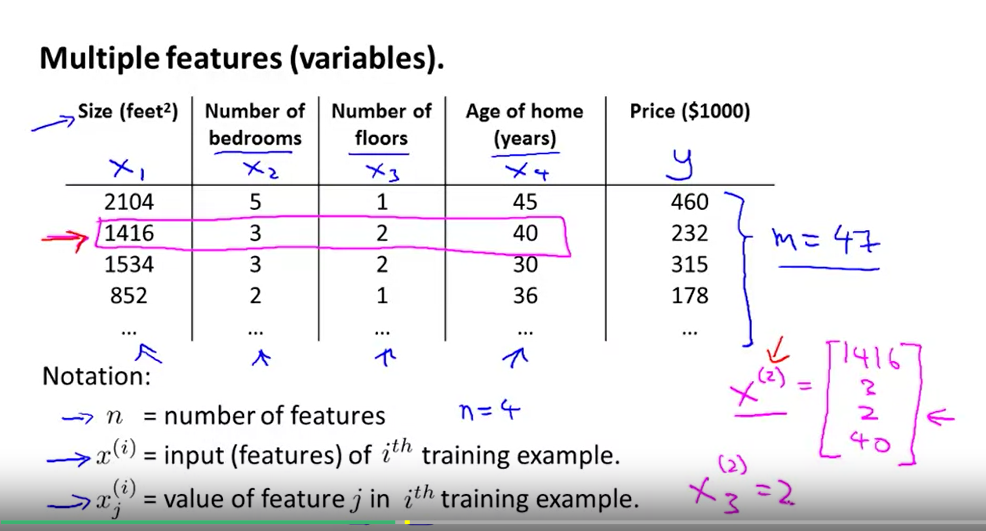





标准化到相近的范围即可
这是因为θ在小范围内下降很快,在大范围内下降很慢,所以当变量非常不均匀时,θ会低效率地振荡到最优。(特征都在一个相近的范围,这样梯度下降法就能更快的收敛)


用X轴上的迭代次数绘制一个图。现在绘制成本函数,J(θ)在梯度下降迭代次数上。如果J(θ)增大,那么可能需要减小α。
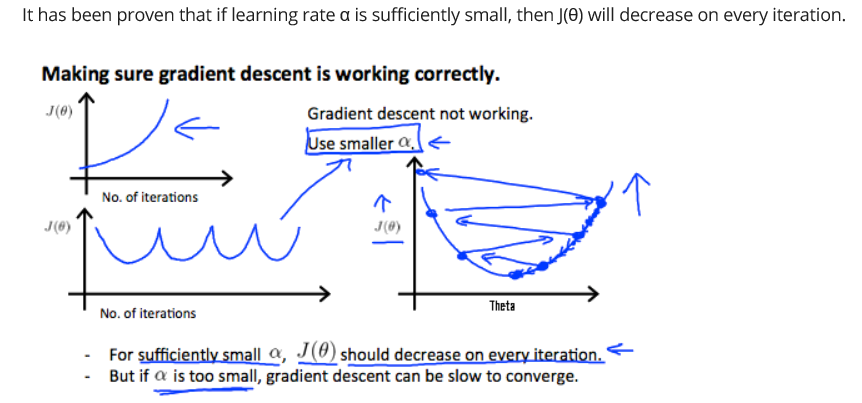
总结一下:
如果α太小:缓慢收敛。
如果α太大:可能不会在每次迭代时减少,因此可能不会收敛。
正规方程
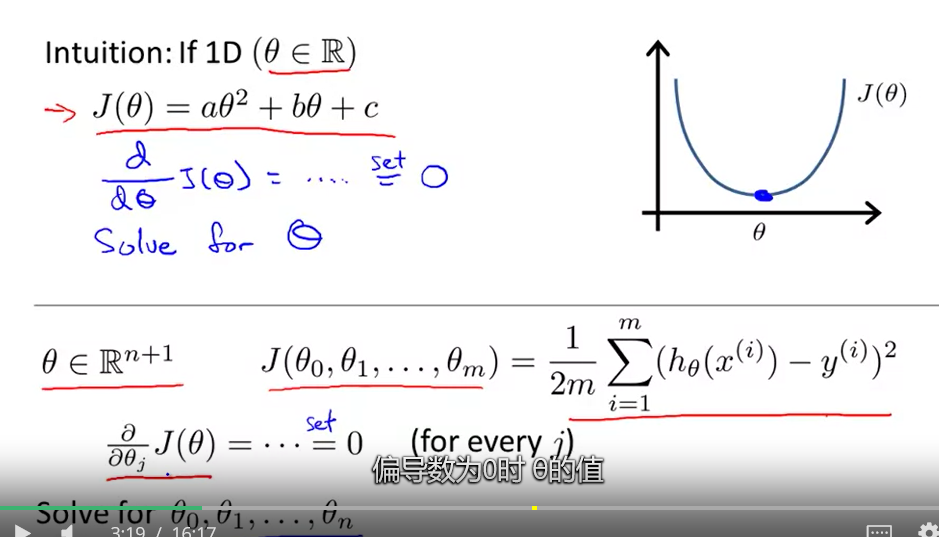


梯度下降和正则方程的区别
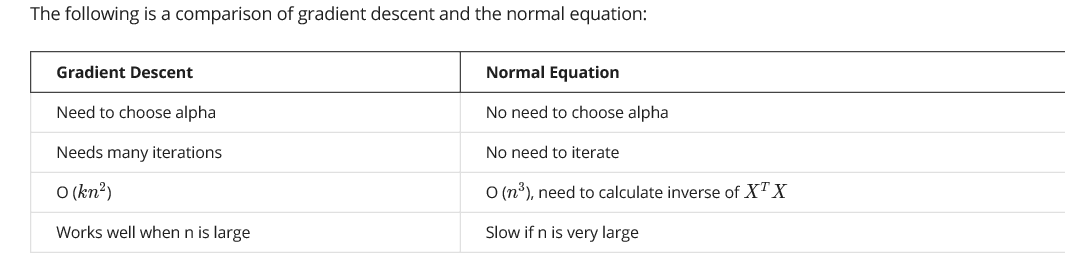
O(n^3):假设X:n*n,当n超过10^4时就不能用正规方程了
使用正则方程不需要归一化特征变量

解决上述问题的方法包括删除与另一个特征线性相关的特征,或者在特征太多时删除一个或多个特征。

