第一个模型,先简化问题,求20以内被7整除的数。
一个自然序列中的数能被7整除,说明以7为周期,序列中有多少个这样的周期就说明有多少个数能被7整除,得到20/7=2。
第二个模型,扩展模型一,假如一个自然序列中的数能被3和7整除,就以3*7=21为周期,序列有多少个这样的周期就说有多少个数被3和7整除,例如:1~100内,能被3和7整除,得到:100/21=4*21+16,这四个数依次为:21,42,63,84,也就是取它们的最小公倍数。

观察规律,第一行,以2,4,1三个数为周期,第二行,以1,4,2,2,4,1,0七个数为周期,根据模型,这两组余数以21为周期,再观察1~21以内有几个余数相同,得到:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | 1 |
| 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 |
在2,4,5,6,10,15位置处,余数相同,一共6个,最后结果得到: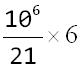
补充:
从余数的周期来看,没有两个余数相加等于0或等于7,所以等式不成立!
补充:
an mod 7的周期列表(其中1<=a<=7)
习题一:在1000内的自然数中,取有序对<x,y>,使得x2+y2能被7整除,(允许重复),有多少对?
解:根据平方的余数周期,能整除7的只有一个,(也即是7的倍数),1000/7=142,有142个数的平方能被7整除。
也可根据允许重复的排列计数方式:从n个元素中取k个,允许重复,一共有nk种可能。
习题二:来源《一百个数学问题》