把圆分成n个不相等的扇形，并且用红，蓝，绿三种颜色给扇形染色，但不许相邻的扇形有相同的颜色，共有多少种染法？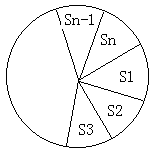
解：设把圆分成扇形S1,S2,...Sn，开始时，S1有3种染法，S1染色后，S2的染法有2种，S3也有2种，因为S3可以和S1同色。
这样的顺次染下去，染色方法的总数为：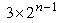
但是这些染法中，还包含Sn与S1同色的情形，设某一种染法使Sn和S1同色，拆去Sn和S1的分界半径OP，则这种染法其实就是分圆为n-1个扇形时同色不相邻的染色。于是得到函数方程：
把圆分成n个不相等的扇形，并且用红，蓝，绿三种颜色给扇形染色，但不许相邻的扇形有相同的颜色，共有多少种染法？解：设把圆分成扇形S1,S2,...Sn，开始时，S1有3种染法，S1染色后，S2的染法有2种，S3也有2种，因为S3可以和S1同色。
这样的顺次染下去，染色方法的总数为：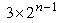
但是这些染法中，还包含Sn与S1同色的情形，设某一种染法使Sn和S1同色，拆去Sn和S1的分界半径OP，则这种染法其实就是分圆为n-1个扇形时同色不相邻的染色。于是得到函数方程：