有一个背包最多可装重量8千克的物品,假设要用该背包装如下水果,要求使背包中装的物品的价值最大,应该装下列哪些物品才能达到要求?
| 物品 | 重量 | 价值 |
| 苹果 | 5千克 | 40元 |
| 梨 | 2千克 | 12元 |
| 桃子 | 1千克 | 7元 |
| 葡萄 | 1千克 | 8元 |
| 香蕉 | 6千克 | 48元 |
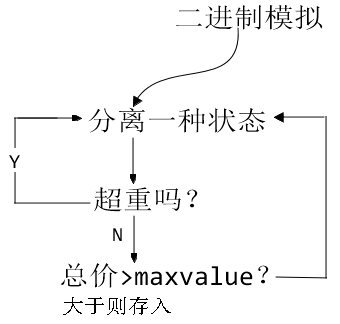
解题思路:首先穷举所有组合可能,有5种物品,一共组合32-1种可能。然后排除超重的可能,在不大于8千克的前提下,再计算各种可能的总价值,最后,比较这些组合的价值,得到最大值。这种思路还是比较简单清晰的。
二进制模拟的概念:对于每个物品,在生成的组合中有两种可能:一是加入背包,二是排除在背包之外,这类有多种物品,每个物品有两种可能的情况,可以使用二进制数来进行模拟。对于n个物品,就可用n位二进制模拟。位为1,表示对应物品加入背包,位为0,表示对应物品不在背包中。
int binadd(char select1[],int n) /*二进制模拟运算*/ { int i,carry=0; select1[0] += 1; for (i = 0; i < n; i++) { select1[i] += carry; //加上进位 carry = select1[i] /2;//计算进位 select1[i] %= 2; //保留0或1? if (carry==0) return 0; } return carry; }
流程:
/*-------完整代码@映雪---------*/ /*初始化一组数据,省略用堆的繁琐,简化流程*/ #include <iostream> using namespace std; typedef struct { int value[5]; int weight[5]; int num; int limitw; }Goods; int bin(int s[],int n) /*二进制模拟运算*/ { int i,carry=0; s[0] += 1; for (i = 0; i < n; i++) { s[i] += carry; //加上进位 carry = s[i] /2;//计算进位 s[i] %= 2; //保留0或1? if (carry==0) return 0; } return carry; } void backpack(Goods *g,int select[])/*计算主程序*/ { int i,flag; int S[5];/*临时状态数组*/ double maxvalue = 0,tw,tv; for (i = 0; i < g->num; i++)//将数组清空 S[i] = 0; while(bin(S, g->num) == 0) //进行一次二进制模拟运算 { tw = 0;/*临时重量*/ tv = 0;/*临时价值*/ flag = 1; for (i = 0; i < g->num; i++) //根据选中状态进行试算 { if (S[i] == 1) //若选中该物品 { tw += g->weight[i]; //累加选中物品的重量 tv += g->value[i];//累加选中物品的价值 if (tw > g->limitw) //超重 { flag = 0; break; //退出本次方案的试算 } } } if(flag && maxvalue < tv) //若方案选中物品重量未超过限制,并且本方案累加价值大于已有方案的最大价值 { maxvalue = tv; for(i = 0; i < g->num; i++) //保存方案(也是更新方案) select[i] = S[i]; } } } int main() { int sumweight,maxvalue; //用来保存阶段最优价值 int select[5]; Goods g={{40,12,7,8,48},{5,2,1,1,6},5,8};/*初始化一组数据*/ backpack(&g,select); sumweight=0; maxvalue=0; printf("可将以下物品装入背包,价值最大: "); for (int i = 0; i < g.num; ++i) if (select[i]) { printf("第%d号物品,重量:%d千克,价值:%d元 ", i + 1, g.weight[i], g.value[i]); sumweight+=g.weight[i]; maxvalue+=g.value[i]; } printf(" 总重量为:%d千克,总价值为:%d元 ", sumweight, maxvalue ); return 0; }