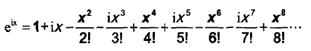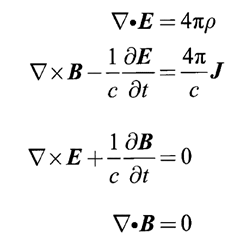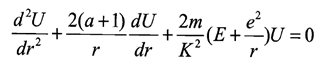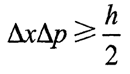第11本:历史上最伟大的10个方程
看此书的主要目的是想了解欧拉公式这个最美的上帝公式的含义,后面的公式越来越难,基本上就不仔细看了。
1、毕达哥拉斯定理(勾股定理)c2=a2+b2
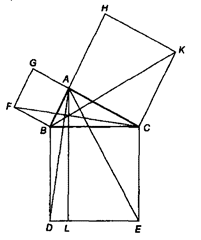
下面这张图是欧几里得《几何原本》中的一个证明的经典图形。
在这个网站http://www.cut-the-knot.org/pythagoras/index.shtml中给出了100多种证明方法,谁有耐心看完,估计几何就学好了。
2、牛顿第二定律F=ma
高一物理课本一上来就讲这个著名的定理。
3、牛顿万有引力定律Fg=Gm1m2/r2
牛顿的苹果的故事估计都听说过。
4、欧拉公式eiπ+1=0
具有数学之美的上帝公式,e和π都是无理数,i是-1的平方根,是一个虚数,0和1是最简单的整数,欧拉公式把它们联系在一起。我看此书的目的就是想了解这个公式的含义,以前在学复变函数时,朦朦胧胧地听过它的含义,一直都没有搞明白过。
实际上e=2.71828…,就是下面这个无穷序数之和。
欧拉在研究三角函数时,发现三角函数也可以用无穷级数来表示。
他引入虚数单位i,把上面2个级数凑在一起。
这个方程在指数函数和三角函数之间建立了深层次的联系。当x=π时,cosπ=-1,sinπ=0,因此eiπ=-1或eiπ+1=0。
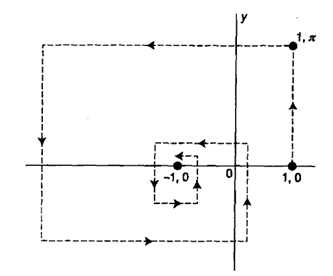
欧拉公式的图形上的含义:
上面每一项都是复平面上的一个向量,也就是把其中的 i 理解为逆时针旋转90度。第一项1表示从(0, 0)点出发沿x轴到达(1, 0)的向量,第2项表示在垂直方向上前进π个单位。第3项就是向左走π2/2个单位。无数级数表示最后的点收敛于(-1, 0)这个点。我终于明白了欧拉公式的几何含义!
5、热力学第二定律S’-S>=0
S表示之前的熵,S’表示一段时间之后的熵。整个世界的熵值向着达到最大值的方向变化。以前对这句话没有什么概念,看了好几本书中都提到了这个观点,现在有一点点理解了。
而热力学第一定律就是说“世界上的能量总量是恒定的”。
后面几个方程我就看不懂了,把公式摆在这里吧。如果能看懂,绝对是一个物理学家。
6、麦克斯韦方程组
我看不懂这个方程。据说它完整描述了包括电磁学在内的物理现象。
7、爱因斯坦质能方程E=mc2
这个也理解不了:能量和质量可以相互转化。能量等于质量乘以光速的平方。
8、爱因斯坦的广义相对论方程
时空决定了物质如何运动,物质决定了时空如何弯曲。
9、薛定谔方程
10、海森促进不确定性定理
英国科学期刊《物理世界》评选的最伟大的公式与这本书的稍有不同,它们是:
No.1 麦克斯韦方程组(The Maxwell's Equations)
No.2 欧拉公式(Euler's Identity)
No.3 牛顿第二定律(Newton's Second Law of Motion)
No.4 勾股定理/毕达哥拉斯定理(Pythagorean Theorem)
No.5 质能方程(Mass–energy Equivalence)
No.6 薛定谔方程(The Schrödinger Equation)
No.7 1+1=2
No.8 德布罗意方程组(The de Broglie Relations)
No.9 傅立叶变换(The Fourier Transform)
No.10 圆的周长公式(The Length of the Circumference of a Circle)