哈希表的原理及实现代码

哈希表可以表述为，是一种可以根据关键字快速查询数据的数据结构

一. 哈希表有哪些优点？

不论哈希表中数据有多少，增加，删除，改写数据的复杂度平均都是O(1)，效率非常高

二. 实现哈希表

1. 哈希表原理

如果说每一个数据它都对应着一个固定的位置，那我们查找特定一个数据时，就可以直接查看这个数据对应的位置是否存在数据。一个形象的例子就是学生在教室中的位置，开学的时候，老师会给学生每一个人分配一个位置，而且不允许学生随便乱坐位置，以后老师要查看今天李刚同学有没有上课，直接看李刚同学的位置是不是有人就可以判断，没必要点了全班同学的名才可以知道李刚同学来了没有。

2. 实现简单的哈希表

根据上面的原理，首先，我们要分配一片空间用来存储我们数据，比如是一个空的数组

然后，有数据存进来的时候，按照特定规则得出这个数据在数组中的位置，将数据存进这个位置

我们就以存进一个整型数据为例，特定规则就是取余

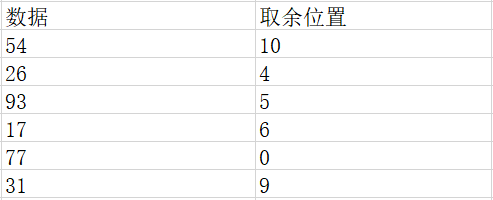
根据计算出来的值，将这些数据放入对应的位置，我们的数组变为

我们已经把数据插入到了哈希表中，现在，我们要查找一个数据，只要按照取余规则计算出这个数据在数组中对应的位置，然后查看数组的这个位置，就可以取出这个数据了，比如我们要从哈希表中取出52，根据取余规则，52的计算出来的位置是8，数组中8这个位置是空的，52不在哈希表中，找不到52的数据；从哈希表中取出77，77计算出来的位置是0，数组中0这个位置有值，而且值就是77，从哈希表中取出77的值。

至此，我们知道实现了一个很简单的哈希表的原理，其实还存在很多问题，这个我们接下来讨论，这儿先把我们前面的一些概念用专业的术语替换一下，前面我们所说的特定规则，我们称之为哈希函数，用特定股则计算出来的值称之为哈希值。

3. 还存在哪些问题？

　　1. 有可能两个数据通过哈希函数计算出来的哈希值有可能相等，比如77，88计算出来的位置值都是0

　　2. 如果哈希表满了，该怎么扩容

第一个问题就是如何解决这种冲突

有开放定址法，链定址法，我们说一下开放定址法，就是将这个冲突的数据再重新计算一个空的位置，将其存进去，比如我们要存放88，哈希值是0，数组这个位置已经有值了，那我们再获取一个哈希值，比如在原哈希值的基础上加1，得到1，1的位置是空，我将88放进去。有人会问，1这个位置被占了，那下一个数据是1这个位置怎么办，这时候，我们还是同样的做法，给这个数据再计算一个哈希值。

插入88后的数组变为

冲突解决了，但我们读取数据的时候，好像又出现问题了，88的哈希值是0，发现数组0位置不是空的，那我们确定88在哈希表中？肯定不行，0这个位置存储的是77，不是88。我们的解决方法是判断0这个位置的值是不是88，不是的话，再计算88的哈希值是1，判断是1这个位置是否为空，为空，则88不在哈希表中；不为空，判断值是否为88，若是88，确定在哈希表中；如果值不是88，我们则继续计算哈希值是2，依次下去，直到找到88或者值为空的位置。

第二个问题，哈希表扩容

一个简单的解决办法是，当插入数据时，发现所有的位置都满了，我们就再分配一个大于原先空间的一片空间，把原来空间中的值重新哈希到新的空间中。

4. 哈希表的python实现

python中的字典就是哈希表，下面代码实现了一个简单的字典

class Dict:
    def __init__(self, size=10):
        self.size = size
        self.key = [None] * self.size
        self.data = [None] * self.size

    def __setitem__(self, key, value):
        assert isinstance(key, int)
        index = self.hash(key)
        if not self.key[index]:
            self.key[index] = key
            self.data[index] = value
        elif self.key[index] == key:
            self.data[index] = value
        else:
            start = index
            while self.key[index] and self.key[index] != key:
                index = self.re_hash(index)
                if index == start:
                    raise Exception('dict is full')

            if self.key[index]:
                self.data[index] = value
            else:
                self.key[index] = key
                self.data[index] = value

    def __getitem__(self, item):
        assert isinstance(item, int)
        index = self.hash(item)
        if not self.key[index]:
            raise KeyError(item)
        else:
            if self.key[index] == item:
                return self.data[index]
            else:
                start = index
                while self.key[index] and self.key[index] != item:
                    index = self.re_hash(index)
                    if start == index:
                        raise KeyError(item)

                if self.key[index] == item:
                    return self.data[index]
                else:
                    raise KeyError(item)

    def __contains__(self, item):
        assert isinstance(item, int)
        index = self.hash(item)
        if not self.key[index]:
            return False
        else:
            if self.key[index] == item:
                return True
            else:
                start = index
                while self.key[index] and self.key[index] != item:
                    index = self.re_hash(index)
                    if start == index:
                        break

                if self.key[index] == item:
                    return True
                else:
                    return False

    def hash(self, key):
        index = key % self.size
        return int(index)

    def re_hash(self, index):
        return index+1


a = Dict()
a[1]='3'
a[2]='4'
print(a[5])

三. 总结：

哈希表对于数据的插入，删除，更新操作复杂的平均是O(1)，效率非常高，如果不关心数据的存储顺序，我们可以选取这种数据结构。