The Doors +0
找出输入的01数列里,0或者1先出完的的下标。
Nirvana +3
输入n,求1到n的数字,哪个数逐位相乘的积最大,输出最大积。
思路是按位比较,从低到高,依次把小位换成全9,判断一下。细节上容易出错,比如边界和减一的情况。要多加小心。
Queen +0
给一棵树,删除树中一些点,这些点的(C_i)权值是1,且直接的孩子也也是1。从小到大依次输出删除的编号。
中间我以为是所有子孙的权值都要是1,幸好发现了。
The Beatles /+0
给一个(n cdot k) 的环,其中每(k)个点就是一个关键点,现在主人公要从某点出发,每次走(l)个距离,最后回到出发点。给出起点距离最近关键点的距离(a),以及第二个到达的位置最近关键点的距离b。最少和最多需要多少次结束活动。
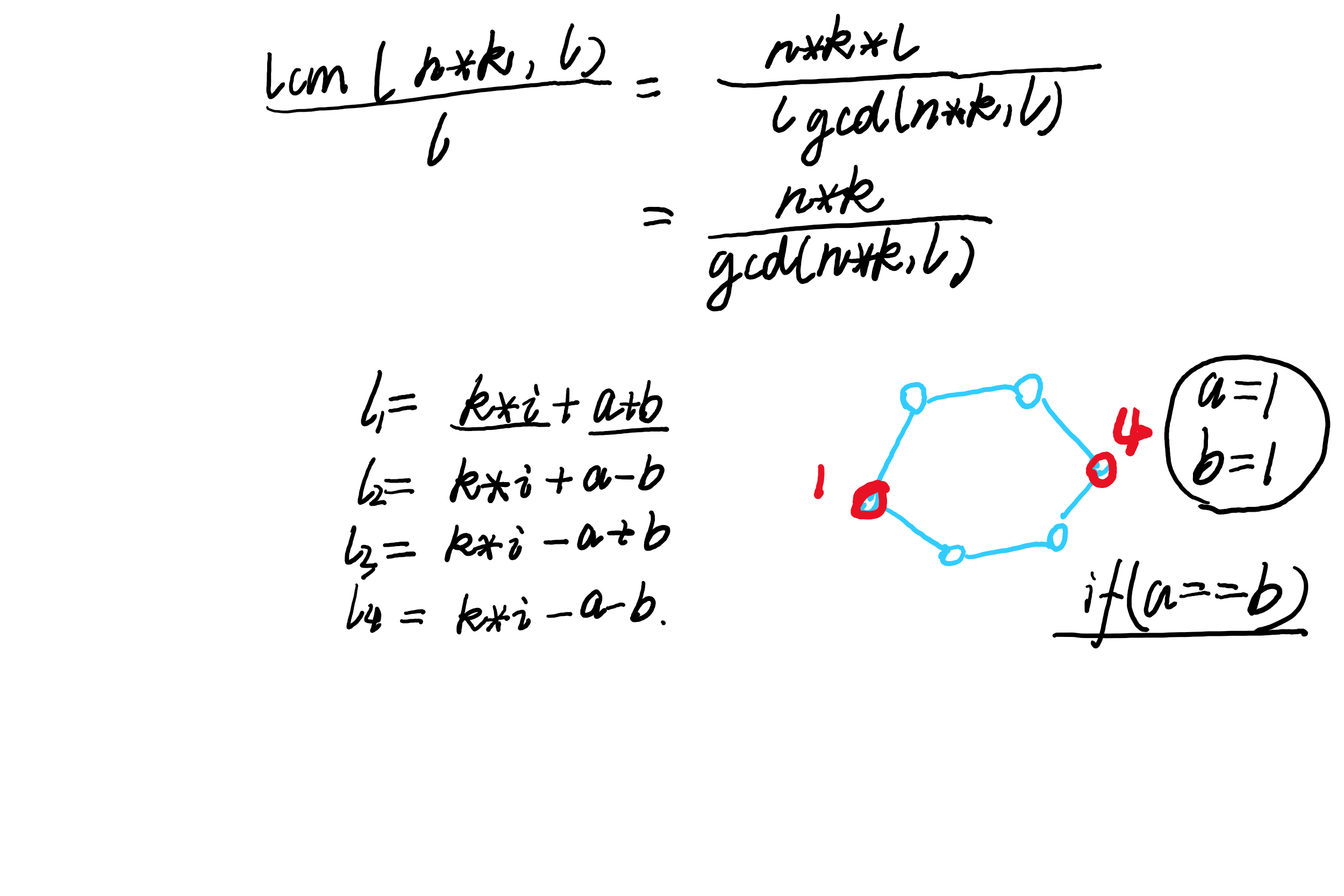
Lynyrd Skynyrd /+0
看过了题解,需要一点倍增(binary lifting)的技巧,大多数时间都用来学倍增了。题意是给长度(n)的数组(p),长度(m)的数组(a),对(a)进行(q)次区间询问,每次判断区间内,是否存在子序列恰好等于(p)的某个cyclic shifts。
cyclic shifts表示把p往左移动若干位,溢出的数依次插到右边。
看上去还挺蒙的,解法要一步步来,首先找到(a[i])的最近的上一个数字(a[j])在什么位置,使得(a[j])和(a[i])恰好是某对(p[k-1])和(p[k]),我们把位置记作(pre[i])。那么我们可以对每个位置(i),往左找(a[i])作为结尾的匹配子序列的起点位置,如果能找到的话,我们可以对每个位置再记一个距离(i)最近的起点,每次询问就可以(O(1))解决。但是这个找起点的过程暴力做的话是显然(n*m)的,时间不允许,因为是连续找前驱的操作,可以用倍增来优化。
//https://codeforces.com/contest/1143/problem/E
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 2e5+7;
const int INF = 0x3f3f3f3f;
int f[MAXN][(int)log(MAXN)+7];
int pre[MAXN];
int p[MAXN],a[MAXN];
int posa[MAXN],posp[MAXN];
int ans[MAXN];
int n,m,q,k;
int findpre(int u){
int t=n-1;
while(t&&u){
for(int i=k;i>=0;i--){
if((1<<i)<=t){
u=f[u][i];
t-=(1<<i);
break;
}
}
}
return u;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
//cout<<log10(100)<<endl;
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
cin>>p[i];
posp[p[i]]=i;
}
for(int i=1;i<=m;i++){
cin>>a[i];
posa[a[i]]=i;
}
for(int pj,i=1;i<=m;i++){
pj=(posp[a[i]]-1+n-1)%n+1;
pre[i]=posa[p[pj]];
posa[a[i]]=i;
}
for(int u=1;u<=m;u++){
f[u][0]=pre[u]<u?pre[u]:0;
}
k=log(n)+1;
for(int i=1;i<=k;i++){
for(int u=1;u<=m;u++){
f[u][i]=f[f[u][i-1]][i-1];
}
}
for(int t,u=n;u<=m;u++){
t=findpre(u);
ans[u]=max(t,ans[u-1]);
}
for(int l,r,i=1;i<=q;i++){
cin>>l>>r;
if(ans[r]>=l)cout<<"1";
else cout<<"0";
}
cout<<endl;
return 0;
}
TBCD...还差一道,咕咕咕
