课后作业1:使用计算机计算组合数:
(1)使用组合数公式利用n!来计算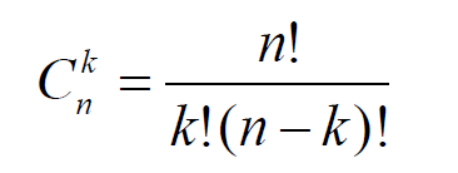
设计思想:用公式的方法求组合数,利用递归方法,求出阶乘n!,k!,(n-k)!,求出组合数的大小。
程序流程图:

源代码:
import java.util.Scanner;
import java.lang.Math.*;
import java.math.BigInteger;
public class Zuheshu
{
public static BigInteger jiecheng(int n)
{
if(n<0)
{
System.out.println("输入有误");
}
if(n==1||n==0)
{
return BigInteger.valueOf(1);
}
else
{
return BigInteger.valueOf(n).multiply(jiecheng((n-1)));
}
}
public static long calculateN(int n)
{
if(n==1 || n==0)
{
return 1;
}
return n*calculateN(n-1);
}
public static void main(String args[])
{
System.out.print("请输入组合数的n和k:");
Scanner scanner1=new Scanner(System.in);//组合数的n
int n=scanner1.nextInt();
Scanner scanner2=new Scanner(System.in);//组合数的k
int k=scanner2.nextInt();
BigInteger x,y,z,d,result;
x=jiecheng(n);
y=jiecheng(k);
z=jiecheng(n-k);
d=y.multiply(z);//计算k!*(n-k)!
result=x.divide(d);//计算n!/(k!*(n-k)!)
System.out.println("组合数的结果是:"+result);//输出运算结果
}
}
结果截图:

(2)使用递推的方法用杨辉三角形计算![]()
设计思想:用递推的方法,由前往后递推,利用杨辉三角形找出规律,利用二元数组求出组合数的大小。
程序流程图:

源代码:
import java.util.Scanner;
import java.lang.Math.*;
public class Zuheshu2
{
public static int n;
public static int k;
public static int c[][]=new int[100][100];
Zuheshu2 a=new Zuheshu2();
public static void main(String args[])
{
System.out.print("请输入组合数的n和k:");
Scanner scanner1=new Scanner(System.in);//组合数的n
int n=scanner1.nextInt();
Scanner scanner2=new Scanner(System.in);//组合数的k
int k=scanner2.nextInt();
c[0][0]=1;//初始化
c[1][0]=1;//初始化
c[1][1]=1;//初始化
for(int i=2;i<=n;i++)
{
c[i][0]=1;
c[i][i]=1;//初始化每行 杨辉三角的两边的值
for(int j=1;j<=i;j++)
{
c[i][j]=c[i-1][j-1]+c[i-1][j];
}
}
System.out.println("组合数的结果是:"+c[n][k]);
}
}
结果截图:

(3)使用递归的方法用组合数递推公式计算
设计思想:用递归函数的方法,由后往前调用递归公式,利用给出的组合数公式,初始化,求出组合数的大小,然后输出结果
程序流程图:

源代码:
import java.util.Scanner;
public class Zuheshu3
{
public static int n;
public static int k;
public static int c[][]=new int[100][100];
public static void main(String args[])
{
System.out.print("请输入组合数的n和k:");
Scanner scanner1=new Scanner(System.in);//组合数的n
int n=scanner1.nextInt();
Scanner scanner2=new Scanner(System.in);//组合数的k
int k=scanner2.nextInt();
c[0][0]=1;//初始化
c[1][0]=1;//初始化
c[1][1]=1;//初始化
System.out.println("组合数的结果是:"+digui(n,k));
}
public static int digui(int n0,int k0)
{
if((k0==n0)||(k0==0))
{
return 1;
}
c[n0][k0]=digui(n0-1,k0)+digui(n0-1,k0-1);
return c[n0][k0];
}
}
结果截图:

课后作业2:
递归编程解决汉诺塔问题。用Java实现
设计思想:递归算法
当n=1时,将A上的盘子直接移动到C上
当n>=2时:
1,将A上n-1个盘子移动到B上(此步骤的解决办法与移动n阶盘子的方法完全一样
只是问题的规模减小1阶
2,将A上的一个盘子移动到C
3,将B上的n-1个盘子移动到C上。
源代码:
import java.util.Scanner;
public class Tower1
{
public static void tower(int n,char one,char two,char three)
{
if(n==1)
{
move(one,three,1);
}
else
{
tower(n-1,one,three,two);
move(one,three, n);
tower(n-1,two,one,three);
}
}
//输出
public static void move(char x,char y, int n)
{
System.out.println(x+"的第"+n+"盘移动到"+y);
}
public static void main(String[] args)
{
int level;
Scanner in = new Scanner(System.in);
System.out.println("请输入层数:");
level = in.nextInt();
Tower1.tower(level,'A','B','C');
}
}
结果截图:

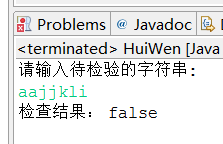
课后作业3:使用递归方式判断某个字串是否是回文
设计思想:利用递归的方法,结合回文的定义,验证字符串是否为回文字符串
程序流程图:

源代码:
package com.resource.test;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class HuiWen
{
/**
* 递归方法判断一个string是否是回文
* 返回true表示当前字符串是一个回文字符串
* 返回false表示该字符串不是回文字符串
* @param args
*/
public static void main(String[] args)throws Exception
{
String str ="";
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in),256);
System.out.println("请输入待检验的字符串:");
str = br.readLine();
System.out.println("检查结果: " + huiwen(str,0,str.length()-1));
}
public static boolean huiwen(String s,int start,int end)
{
if(start == end) return true;
if(start > end)
{
System.out.println("您没有输入任何字符串!");
return false;
}
if(s.charAt(start) == s.charAt(end))
{
return huiwen(s,start+1,end-1);
}
else
{
return false;
}
}
}
结果截图