什么是“迪杰斯特拉(Dijkstra)”算法?
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
用来解决什么样的问题?
解决的是有权图中最短路径问题,给定带权有向图G=(V, E)和源点v∈V,求从v到G中其余各顶点的最短路径
应用案例:
1.计算机网络传输的问题:怎样找到一种最经济的方式,从一台计算机向网上所有其它计算机发送一条消息。
2.交通运输问题,走那条路径最优
解决思路步骤
基本思想:设置一个集合S存放已经找到最短路径的顶点,S的初始状态只包含源点v,对vi∈V-S,假设从源点v到vi的有向边为最短路径。以后每求得一条最短路径v, …, vk,就将vk加入集合S中,并将路径v, …, vk , vi与原来的假设相比较,取路径长度较小者为最短路径。重复上述过程,直到集合V中全部顶点加入到集合S中。
设计数据结构 :
1、图的存储结构:带权的邻接矩阵存储结构 。
2、数组dist[n]:每个分量dist[i]表示当前所找到的从始点v到终点vi的最短路径的长度。初态为:若从v到vi有弧,则dist[i]为弧上权值;否则置dist[i]为∞。
3、数组path[n]:path[i]是一个字符串,表示当前所找到的从始点v到终点vi的最短路径。初态为:若从v到vi有弧,则path[i]为vvi;否则置path[i]空串。
4、数组s[n]:存放源点和已经生成的终点,其初态为只有一个源点v。
详细步骤及相关说明
迪杰斯特拉算法(详细)
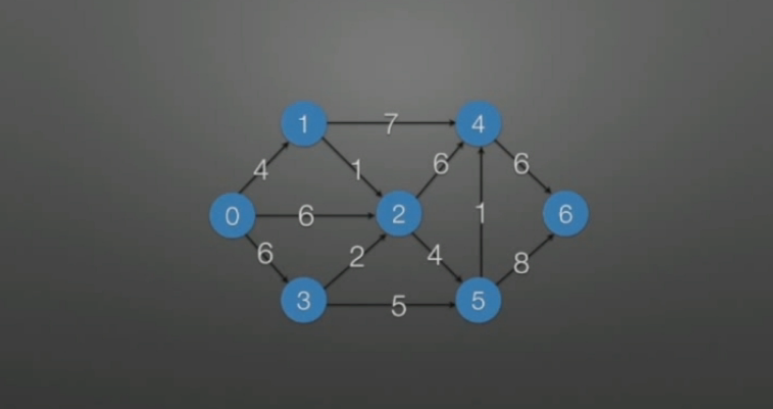
Dist :存储了当前起点到其余各顶点的最短路径长度
Path :存储了起点到其余各顶点的路径
Set:标记了哪些顶点已经被选入了最短路径
说明:
+:表示起点到顶点没有直接相连
-1:当前顶点在其最短路径上面没有前一个顶点或者没有关系
初始状态
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
6 |
6 |
+ |
+ |
+ |
|
Path |
-1 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
|
Set |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
从某个定点到其余各个顶点的最短路径
选择距离起点最近的那个顶点,将其并入,然后扫描图中未被并入顶点的所有顶点。
当前从“起点0”到“当前顶点V”,就是dist数组中的值,然后看看从0经过刚并入顶点的到v的长度,如果:L(0- 刚并入顶点-V) < L(0-V),此时就更新起点0到V的最短路径距离为L(0- 刚并入顶点-V),然后更新Path中V的值为”刚并入顶点的序号”,否则不做更改。
L(0- 刚并入顶点-V) < L(0-V)
起点直接到某一个顶点长度:Dist值
这里的直接:不是指有直接的边相连,这里的直接指的是“经过上一次更新由起点不经过刚并入顶点到(顶点)4的最短路径”。
终结点到顶点:必须是一条直接的边,尽管之间有一条路径,若不是直接相连也认为两者之间的距离为无穷大。
第1次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
5 |
6 |
11 |
+ |
+ |
|
Path |
-1 |
0 |
1 |
0 |
1 |
-1 |
-1 |
|
Set |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
第2次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
6 |
6 |
+ |
+ |
+ |
|
Path |
-1 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
|
Set |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
第3次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
5 |
6 |
11 |
9 |
+ |
|
Path |
-1 |
0 |
1 |
0 |
1 |
2 |
-1 |
|
Set |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
第4次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
5 |
6 |
10 |
9 |
17 |
|
Path |
-1 |
0 |
1 |
0 |
5 |
2 |
5 |
|
Set |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
第5次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
5 |
6 |
10 |
9 |
16 |
|
Path |
-1 |
0 |
1 |
0 |
5 |
2 |
4 |
|
Set |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
第6次
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Dist |
0 |
4 |
5 |
6 |
10 |
9 |
16 |
|
Path |
-1 |
0 |
1 |
0 |
5 |
2 |
4 |
|
Set |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
综上可得:0-其余各顶点的最短路径
0-6的路径为:0-1-2-5-4-6
未完待续:后面加入“弗洛伊德(Floyd)”算法