直接插入排序(顺序插入排序)
基本思想:
排序过程,整个排序过程为n-1趟插入,即先将序列中的第1个元素看成是一个有序子序列,然后从第2个元素开始,逐个进行插入,直至整个序列有序。
在有序序列中插入一个元素,保持序列是有序的,不断增长这个有序序列完成排序
就类似将成绩单上的第一个同学的名字和成绩学到旁边一张白纸中央,如果第二个同学比他成绩高,就写到第一个同学的上方,如果比他低,就写到下方。等看到第三个同学的成绩后,根据他的成绩与前两个同学成绩比较,插入到相应的位置。比如他的成绩正好在两个同学之间,就在傍边那张纸上,把他的名字插入到前两个人之间。当然,那张排序的张要留够足够的空白,方便插入后来的同学名字。
public static void Insert_sort(int[] a) { for (int i = 1; i < a.Length; i++) { int temp = a[i]; //将待排序的数组存入临时变量 int j; for (j = i - 1; j >= 0 && temp<a[j]; j--) { a[j + 1] = a[j]; //将小的数值往后移 } a[j + 1] = temp; //将未排序的数字插入到相应的位置 } }
折半插入排序(二分插入排序)
基本思想:
折半插入算法是对直接插入排序算法的改进,排序原理同直接插入算法:
把n个待排序的元素看成一个有序表和一个无序表,开始时有序表中只有一个元素,无序表中有n-1个元素;排序过程即每次从无序表中取出第一个元素,将它插入到有序表中,使之成为新的有序表,重复n-1次完成整个排序过程。
public static void BinaryInsertSort(int[] arr) { for (int i = 1; i < arr.Length; i++) //依次从第1个元素到第n个元素插入到有序序列中 { int temp = arr[i]; //将待排序的数值赋值给一个变量 int mid = 0; //有序序列数组的中间位置 int low = 0; //有序序列中的第一个元素 int high = i-1; //有序序列中的第最后个元素 //采用二分法在有序的的数组序列中不断循环找到合适的插入位置 while (low <= high) { mid = (low + high);//计算出中间位置 //如果待排序的数值小于中间值则在左半部分查找插入位置 //否则在右半部分查找插入位置 if (temp < arr[mid]) { high = mid - 1; } else { low = mid + 1; } } //将需要移动的数组向后移 for (int j = i - 1; j < high + 1; j--) { arr[j + 1] = arr[j]; } //需要插入的下标位置,i待排序的下标位置 if (low != i) { arr[low] = temp; } } }
希尔插入排序(缩小增量排序)
基本思想:
- 假设待排序元素序列有n个元素,首先取一个整数increment(小于n)作为间隔将全部元素分为increment个子序列,所有距离为increment的元素放在同一个子序列中,在每一个子序列中分别实行直接插入排序。然后缩小间隔increment,重复上述子序列划分和排序工作。直到最后取increment=1,将所有元素放在同一个子序列中排序为止。
- 由于开始时,increment的取值较大,每个子序列中的元素较少,排序速度较快,到排序后期increment取值逐渐变小,子序列中元素个数逐渐增多,但由于前面工作的基础,大多数元素已经基本有序,所以排序速度仍然很快。
- 关于希尔排序increment(增量)的取法增量increment的取法有各种方案。最初shell提出取increment=n/2向下取整,increment=increment/2向下取整,直到increment=1。但由于直到最后一步,在奇数位置的元素才会与偶数位置的元素进行比较,这样使用这个序列的效率会很低。后来Knuth提出取increment=n/3向下取整+1.还有人提出都取奇数为好,也有人提出increment互质为好。应用不同的序列会使希尔排序算法的性能有很大的差异。
static void shell_sort(int[] arr) { int d=(arr.Length)/2; while(d>=1) { for(int i=d;i<arr.Length;i++) { int temp=arr[i]; int j=i-d; //直接插入排序,会向前找所适合的位置 while(j>=0&&arr[j] >temp) { //交换位置 arr[j+d]=arr[j]; j=j-d; } arr[j+d]=temp; } d/=2; } }
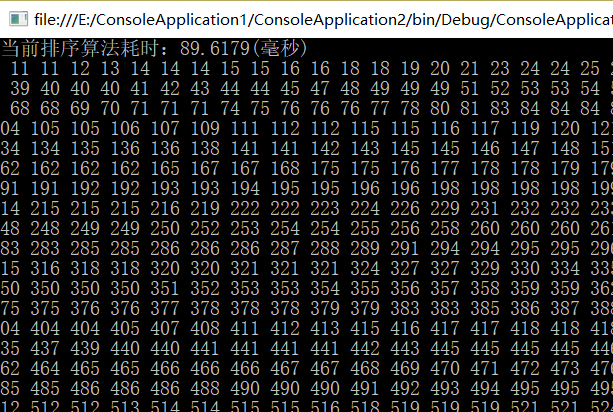
随机向数组中存入10万个元素比较耗时。
有关测试结果
直接插入排序:
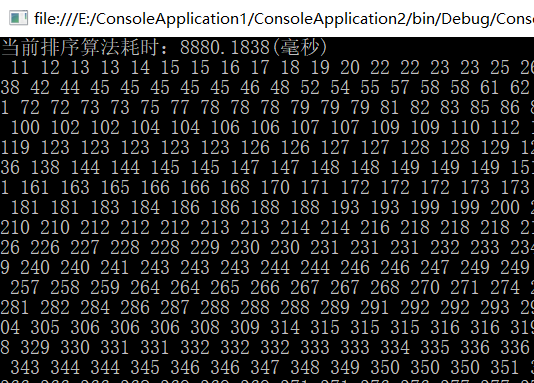
折半插入排序:
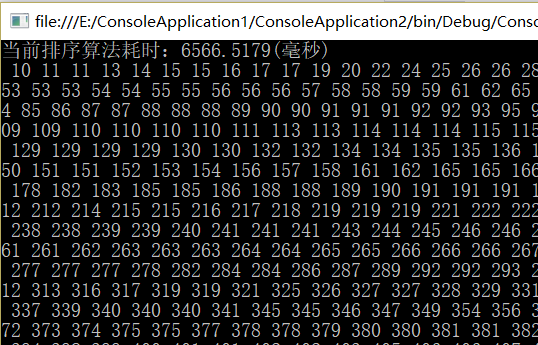
希尔排序: