K-means算法的实现

K-MEANS算法是一种经典的聚类算法，在模式识别得到了广泛的应用。算法中有两个关键问题需要考虑：一是如何评价对象的相似性，通常用距离来度量，距离越近越相似；另外一个是如何评价聚类的效果，通常采用误差平方和函数来作为评价准则。

算法过程：

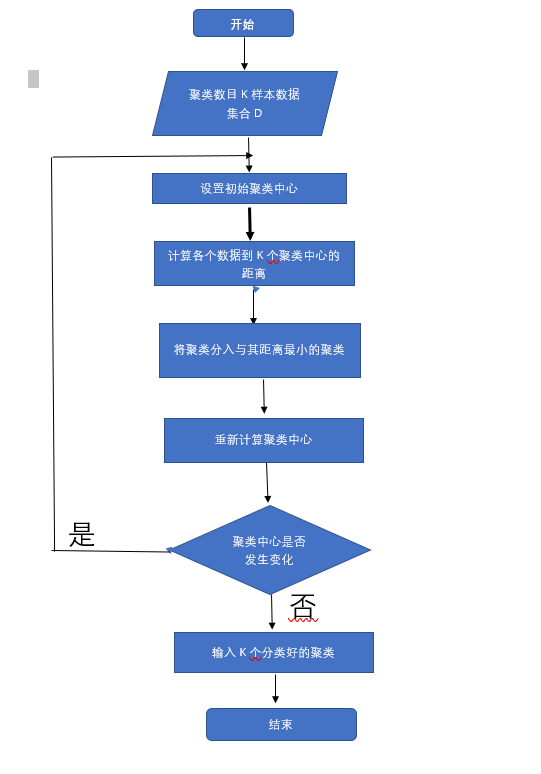
输入：簇的数目K和包含n个对象的数据库。

输出：K个簇，使平方误差和最小

算法步骤：

（1):为每个聚类确定一个初始聚类中心，这样就有K个初始聚类中心

（2:将样本集中的样本按照最小距离原则分配到最邻近聚类

（3);使用每个聚类中的样本均值作为新的聚类中心

 (4):重复步骤(2)和(3),直到聚类中心不在变化

(5):结束，得到K个聚类

流程图

代码实现

import numpy
import random
import codecs
import copy
import re
import matplotlib.pyplot as plt
#其次计算向量vecl和向量vec2之间的欧式距离
def calcuDistance(vec1,vec2):
    return numpy.sqrt(numpy.sum(numpy.square(vec1-vec2)))
#载入数据测试数据集，数据由文本保存，为二维坐标
def loadDataSet():
    inFile = "F:/testSet.txt"  #数据集文件
    inDate = codecs.open(inFile,'r','utf-8').readlines()
    dataSet = list()
    for line in inDate:
        line = line.strip()
        strList = re.split('[ ]+',line) #删除多余的空格
                                        #print strList[0] ,strList[1]
        numList = list()
        for item in strList:
            num = float(item)
            numList.append(num)

        dataSet.append(numList)
    return dataSet

#初始化K个聚类中心，随机获取
def initCentroids(dataSet,k):
    return random.sample(dataSet,k)#从dataSe中随机获取K个数据项返回
#对每个属于dataSet的item，计算item与centrodList中K个聚类中心的欧式距离，找出
#距离最小的，并将item加入相应的簇中
def minDistance(dataSet,centroidList):
    clusterDict = dict()  #用dict来保存聚类的结果
    for item in dataSet:
        vec1 = numpy.array(item) #转换成array形式
        flag = 0     #簇分类标记，记录与相应的簇距离最近的那个簇
        minDis = float("inf") #初始化为最大值
        for i in range(len(centroidList)):
            vec2 = numpy.array(centroidList[i])
            distance = calcuDistance(vec1,vec2) #计算相应的欧拉距离
            if distance < minDis:
                minDis = distance
                flag = i  #循环结束时，flag保存的是与当前item距离最近的那个簇标记
        if flag not in clusterDict.keys():#簇标记不存在，进行初始化
            clusterDict[flag] = list()
            clusterDict[flag].append(item) #加入相应的类别中
        return clusterDict

#计算每列的均值，即找到聚类中心
def getCentroids(clusterDict):
    #得到K个质心
    centroidList = list()
    for key in clusterDict.keys():
        centroid = numpy.mean(numpy.array(clusterDict[key]),axis=0)
        centroidList.append(centroid)
    return numpy.array(centroidList).tolist()
#计算簇集合间的均方误差，将簇类中各个向量与质心的距离进行累加求和
def getVar(clusterDict,centroidList):
    sum = 0.0
    for key in clusterDict.keys():
        vec1 = numpy.array(centroidList[key])
        distance = 0.0
        for item in clusterDict[key]:
            vec2 = numpy.array(item)
            distance += calcuDistance(vec1,vec2)
        sum += distance
    return sum

#展示聚类结果
def showCluster(centroidList,clusterDict):
    colorMark = ['or','ob','og','ok','oy','ow']
    #不同簇类的标记，'or'-->'o'代表圆形，’r'代表red，‘b’：blue
    centroidMark = ['dr','db','dg','dk','dy','dw'] #簇类中心标记同上‘d’代表菱形
    for key in clusterDict.keys():#画簇类中心点
        plt.plot(centroidList[key][0],centroidList[key][1],centroidMark[key],markersize=12)
        for item in clusterDict[key]:
            plt.plot(item[0],item[1],colorMark[key])#画簇类下的点
    plt.show()

if __name__=='__main__':
#    inFile = "F:/testSet.txt"  #数据集文件
    dataSet = loadDataSet() #载入数据集
    centroidList = initCentroids(dataSet,4) #初始化质心，设置K=4
    clusterDict = minDistance(dataSet,centroidList) #第一次聚类迭代
    newVar = getVar(clusterDict,centroidList) #获得均方误差值，通过新旧均方误差来获得迭代终止条件
    oldVar = -0.0001 #旧均方误差值初始化为-1
    print("------第一次迭代------")
    print( )
    print("簇类")
    for key in clusterDict.keys():
        print(key,'---->',clusterDict[key])
    print("K个均值向量：",centroidList)
    print("平方均方误差：",newVar)
    print( )
    showCluster(centroidList,clusterDict) #展示聚类结果
    k = 2
    while abs(newVar-oldVar) >= 0.0001: #当两次聚类结果小于0.0001时，迭代结束
        centroidList = getCentroids(clusterDict) #获得新的质心
        clusterDict = minDistance(dataSet,centroidList) #新的聚类结果
        oldVar = newVar
        newVar = getVar(clusterDict,centroidList)
        print("----第%d次迭代结果--------" %k)
        print( )
        print("簇类")
        for key in clusterDict.keys():
            print(key, '---->', clusterDict[key])
        print("K个均值向量：", centroidList)
        print("平方均方误差：", newVar)
        print()
        showCluster(centroidList, clusterDict)  # 展示聚类结果
        k += 1

目前，对于聚类算法的理解还不是很深刻。正在慢慢探索中。