
这是一道典型的求一个凸多边形面积的题,对于求解凸多边形面积,通常的思路就是将该多边形分割成多个可解的简单多边形,例如三角形或者矩形。
对于连续和非连续的分布,分别可以采用积分法和三角形点分割的方式进行求解。
对于本题,易知是多个非连续的点集合,而且点的排序方式为逆时针,这是一个非常关键的假设,根据该假设我们可以把该多边形一次分割成多个相邻的不重叠三角形,再利用三角形面积公式递归求解
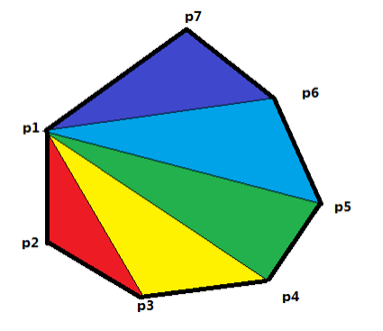
上图是分割的一个示例图,通过一次分割,可将原凸七边形分割成5个相邻的三角形,接下来我们引入通过三顶点坐标求解三角形面积的公式:
若已知一个三角形的三个顶点坐标分别为: (x1,y1)(x2,y2)(x3,y3) 则该三角形的面积可以表示为:

#include<stdio.h>
int main()
{
int n,i;
double s,f[100][2];
while(~scanf("%d",&n)&&n)
{
double s=0.0;
for(i=0;i<n;i++)
{
scanf("%lf %lf",&f[i][0],&f[i][1]);
}
for(i=2;i<n;i++)
{
s=s+((f[i-1][0]-f[0][0])*(f[i][1]-f[0][1])-(f[i][0]-f[0][0])*(f[i-1][1]-f[0][1]));
}
s=s/2.0;
printf("%.1lf
",s);
}
return 0;
}