原始算法是sphere,我这里简化为circle了。
Ritter's求最小包围圆为线性算法,因为非常简单,所以应用非常广泛。
该算法求出的圆比最优圆大概会大个5%到20%左右,求最优圆应该可以用Bouncing Bubble算法,以后有机会可以尝试一下。
Ritter's算法如下:
1.从点集中随机选出两个点作为直径对圆进行初始化。
2.判断下一个点p是否在圆中,如果在则继续本步骤,如果不在则进行步骤3。
3.使用p作为新圆的一个边界点,另一个边界点为距离p最远的圆上的点,使用这两个点作为直径构造新圆。
4.继续步骤2,直到遍历完所有点。
结果如下:
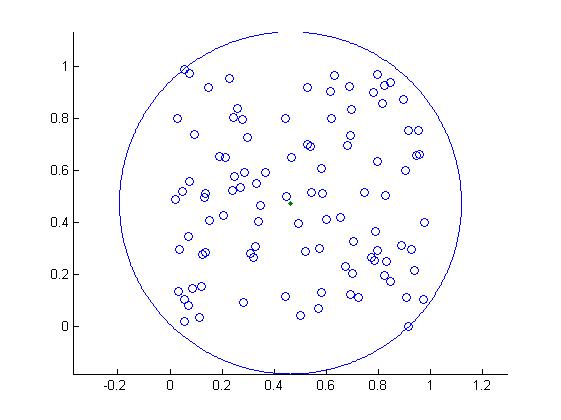
matlab代码如下:
clear all;close all;clc; n=100; p=rand(n,2); p1=p(1,:); p2=p(2,:); r=sqrt((p1(1)-p2(1))^2+(p1(2)-p2(2))^2)/2; cenp=(p1+p2)/2; for i=3:n newp=p(i,:); d=sqrt((cenp(1)-newp(1))^2+(cenp(2)-newp(2))^2); if d>r r=(r+d)/2; cenp=cenp+(d-r)/d*(newp-cenp); end end hold on; plot(p(:,1),p(:,2),'o'); x0=cenp(1); y0=cenp(2); theta=0:0.01:2*pi; x=x0+r*cos(theta); y=y0+r*sin(theta); plot(x,y,'-',x0,y0,'.'); axis equal