该方法是自抗扰控制器adrc中的一个步骤,这里单独拿出来实现一下。
算法输入为控制信号,输出为微分信号和跟踪信号,能够滤除控制信号中的噪声。
跟踪微分器核心公式如下:
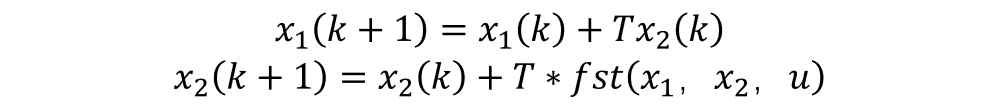
fst函数如下:
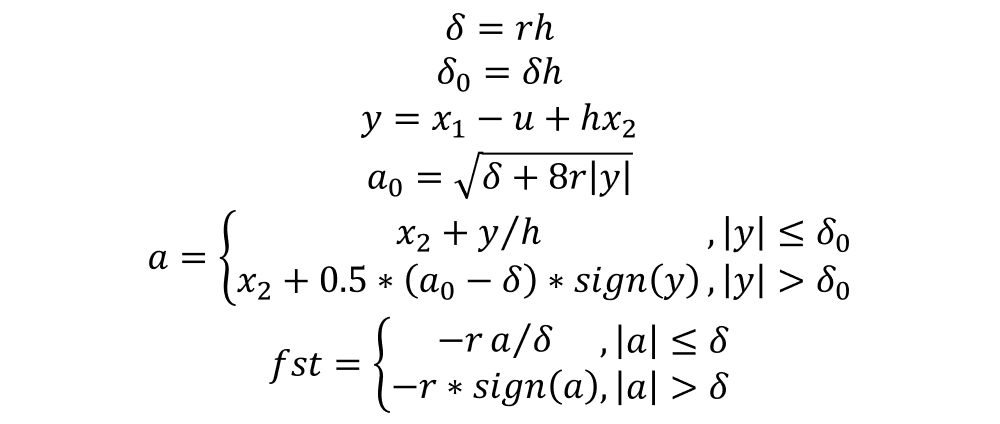
其中u为控制量,r和h为系数。
matlab代码如下:
clear all;close all;clc; T = 0.01; x = 0:0.01:10; u = double(x>5); plot(x,u,'g'); hold on; u = u + rand(length(u),1)'*0.2 - 0.1; %叠加噪声 plot(x,u,'b'); x1k = 0;x2k = 0; x1 = 0; x2 = 0; re = zeros(length(x),2); for i=1:length(x) x1k = x1; x2k = x2; x1 = x1k + T * x2k; x2 = x2k + T * fst(x1k,x2k,u(i)); re(i,:) = [x1 x2]; end hold on; plot(x,re(:,1),'r'); plot(x,re(:,2),'m') legend('原始信号','叠加噪声信号','跟踪信号','微分信号') function f = fst(x1,x2,u) r = 10; h = 0.1; delta = r * h; %h为滤波因子 r为调节系数,r越大跟踪效果越好,但微分信号会增加高频噪声 delta0 = delta * h; %反之,微分信号越平滑,会产生一定的滞后 y = x1 - u + h * x2; a0 = sqrt(delta^2 + 8 * r * abs(y)); if abs(y)<=delta0 a = x2 + y / h; else a = x2 + 0.5 * (a0-delta) * sign(y); end if abs(a)<=delta f = -r * a/delta; else f = -r * sign(a); end end
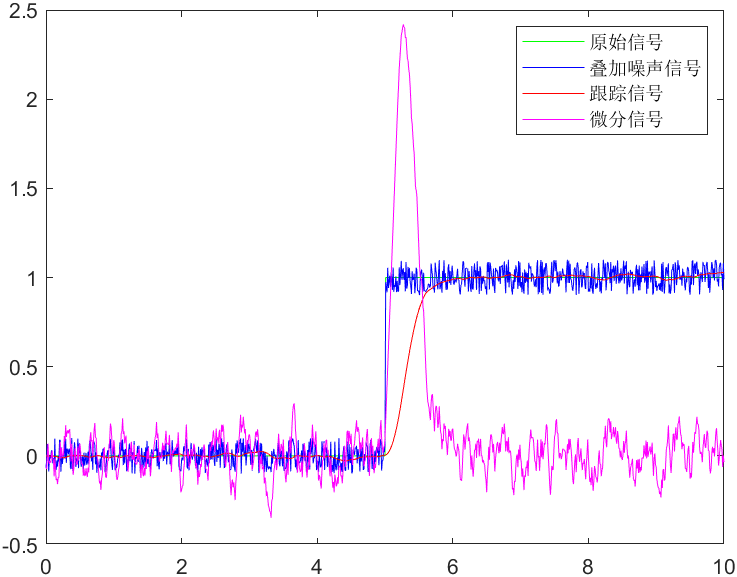
结果如下:
参考:https://blog.csdn.net/m0_37764065/article/details/108668033