matlab练习程序（离散系统辨识与响应）

上一篇熟悉了连续系统辨识与响应，这一篇熟悉一下离散系统辨识与响应。

计算机通常处理的系统为离散系统，这里我们先将连续系统转换为离散系统，然后再进行处理。

流程上还是先构造离散系统并根据控制量得到响应，然后用子空间迭代算法（以后会单独实现一次）求出状态空间。

再用识别得到的状态空间和原始控制量生成新的响应，并比较结果。

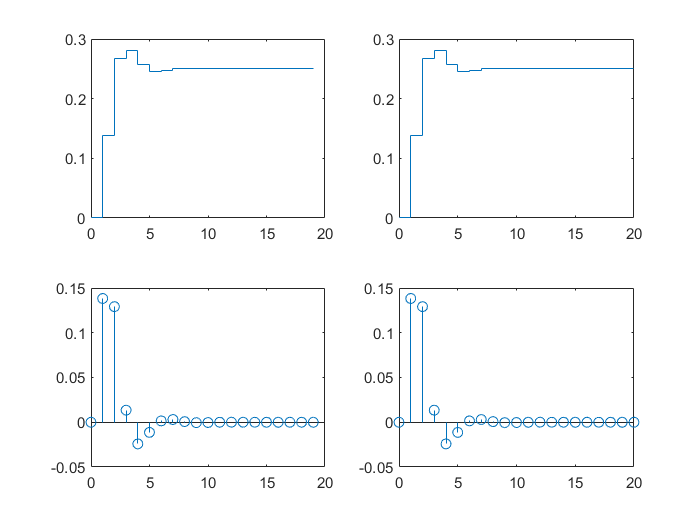
最后再比较一下阶跃和冲击响应。

matlab代码如下：

clear all;close all;clc;

load dryer2
warning off;

A = [-1.5,-2;1,0];
B = [0.5;0];
C = [0,1];
D = 0;
sys = ss(A,B,C,D);              %状态方程
sysd = c2d(sys,1);              %转为离散
sysd_tf = tf(sysd);             %传递函数

u = u2(1:100);                  %控制量
x = [0;0];                      %系统初始状态
for i = 1:100
    x(:,i+1) = sysd.A * x(:,i) + sysd.B * u(i);
    y(i) = sysd.C*x(:,i) + sysd.D*u(i);
end
plot(y,'r-*');

%%%%%%%%%%%%%%%%%%%%%%%%离散系统辨识%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
idata = iddata(y',u);            %构造辨识结构体
idsys = n4sid(idata);            %系统辨识得到状态方程(离散)
idsys_tf = idtf(idsys);

x = [0;0];                       %系统初始状态
for i = 1:100
    x(:,i+1) = idsys.A * x(:,i) + idsys.B * u(i);
    y(i) = idsys.C*x(:,i) + idsys.D*u(i);
end
hold on;
plot(y,'go')

%%%%%%%%%%%%%%%%%%%%%%%%离散系统状态空间转传递函数%%%%%%%%%%%%%%%%%%%%%%%%%%
syms z;
Gz = sysd.C*inv(z*eye(2) - sysd.A)*sysd.B+sysd.D;
digits(5)

GGz= vpa(Gz);
GGz = simplify(GGz);

%三种方法求出的传递函数
sysd_tf
idsys_tf
GGz

%%%%%%%%%%%%%%%%%%%%%%%%离散系统阶跃响应%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x = [0;0];                      %系统初始状态
u = ones(20,1);
y = zeros(20,1);
for i = 1:20
    x(:,i+1) = idsys.A * x(:,i) + idsys.B*u(i);
    y(i) = idsys.C*x(:,i) + idsys.D*u(i);
end
figure;

subplot(2,2,1);
stairs((1:20)-1,y);
subplot(2,2,2);
[r,t] = step(idsys);
stairs(t,r);

%%%%%%%%%%%%%%%%%%%%%%%%离散系统冲击响应%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x = [0;0];                      
u = zeros(20,1);
y = zeros(20,1);
u(1) = 1;
for i = 1:20
    x(:,i+1) = idsys.A * x(:,i) + idsys.B*u(i);
    y(i) = idsys.C*x(:,i) + idsys.D*u(i);
end
subplot(2,2,3);
stem((1:20)-1,y);
subplot(2,2,4);
[r,t] = impulse(idsys);
stem(t,r);

结果如下：

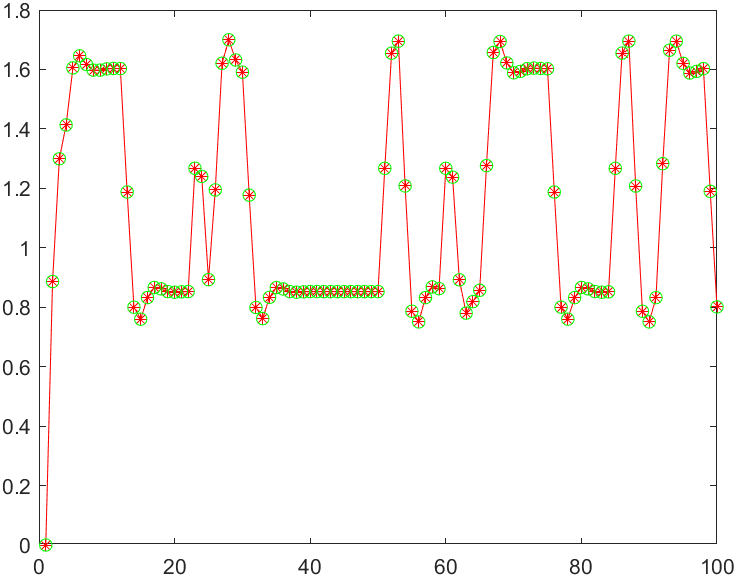
用原控制量与辨识结果生成响应：

 

阶跃与冲击响应：