网络流24题-骑士共存问题

骑士共存问题

时空限制1000ms / 128MB

题目描述

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

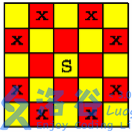
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入输出格式

输入格式：

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

输出格式：

将计算出的共存骑士数输出

输入输出样例

输入样例： 

3 2
1 1
3 3

输出样例： 

5

说明

题目链接：https://www.luogu.org/problemnew/show/P3355

---

这一题和方格取数问题思路是一样的。当时我还没学二分图最大点权独立集，所以强行理解了一波最小割（emmmm）。如果对图进行黑白染色，使白格只与黑格相邻，黑格只与白格相邻，则观察发现任何互相冲突的两个骑士一定属于不同颜色的格子，于是这题就变成了很裸的二分图最大点权独立集。

还有一个很蠢的问题：我以前一直以为网络流跑二分图相关问题的时候，对于二分图无论是加双向边还是单向边对算法没有影响，结果今天WA到我怀疑人生。。。。。。理性分析一下发现不能建双向边，因为这样的话有可能会把某些不能形成流的情况强行形成流，因此这种网络流的题目还是有一个全局流向的概念比较好，然后按照这个全局流向来建边。

#include<bits/stdc++.h>
#define INF LLONG_MAX/2
#define N 40050
using namespace std;

struct ss
{
    int v,next;
    long long flow;
};
int head[N],now_edge=0,S,T;
ss edg[N*32];

void init()
{
    now_edge=0;
    memset(head,-1,sizeof(head));
}

void addedge(int u,int v,long long flow)
{
    edg[now_edge]=(ss){v,head[u],flow};
    head[u]=now_edge++;
    edg[now_edge]=(ss){u,head[v],0};
    head[v]=now_edge++;
}

int dis[N];

int bfs()
{
    memset(dis,0,sizeof(dis));
    queue<int>q;
    q.push(S);
    dis[S]=1;

    while(!q.empty())
    {
        int now=q.front();
        q.pop();

        for(int i=head[now];i!=-1;i=edg[i].next)
        {
            ss &e=edg[i];
            if(e.flow>0&&dis[e.v]==0)
            {
                dis[e.v]=dis[now]+1;
                q.push(e.v);
            }
        }
    }

    if(dis[T]==0)return 0;
    return 1;
}

int current[N];
long long dfs(int x,long long maxflow)
{
    if(x==T)return maxflow;
    for(int i=current[x];i!=-1;i=edg[i].next)
    {
        current[x]=i;

        ss &e=edg[i];
        if(e.flow>0&&dis[e.v]==dis[x]+1)
        {
            long long flow=dfs(e.v,min(maxflow,e.flow));

            if(flow!=0)
            {
                e.flow-=flow;
                edg[i^1].flow+=flow;
                return flow;
            }
        }
    }
    return 0;
}

long long dinic()
{
    long long ans=0,flow;

    while(bfs())
    {
        for(int i=0;i<N;i++)current[i]=head[i];
        while(flow=dfs(S,INF))ans+=flow;
    }
    return ans;
}

int color[205][205]={0};
int num[205][205];
int Map[205][205]={0};
int n;

int check(int x,int y)
{
    if(x<=0||x>n||y<=0||y>n||Map[x][y])return 0;
    return 1;
}

int fx[10]={-2,-2,-1,1,2,2,1,-1};
int fy[10]={-1,1,2,2,1,-1,-2,-2};

int main()
{
    init();
    int m,cnt=1;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)num[i][j]=cnt++;
    S=cnt;
    T=S+1;
    
    for(int i=1;i<=n;i++)
    for(int j=(i%2==0 ? 2 : 1);j<=n;j+=2)color[i][j]=1;
    
/*    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        printf("%d",color[i][j]);
        printf("
");
    }*/
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d %d",&x,&y);
        Map[x][y]=1;
    }
    
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    if(!Map[i][j]&&color[i][j])
    {
        for(int k=0;k<8;k++)
        if(check(i+fx[k],j+fy[k]))
        {
            addedge(num[i][j],num[i+fx[k]][j+fy[k]],INF);
        }
    }
    
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    if(!Map[i][j])
    {
        if(color[i][j])addedge(S,num[i][j],1);
        else
        addedge(num[i][j],T,1);
    }
    
    printf("%lld
",(long long)n*n-dinic()-m);
    return 0;

}