时空限制1000ms-2000ms / 300MB
题目背景
公元 2044 年,人类进入了宇宙纪元。
题目描述
公元2044 年,人类进入了宇宙纪元。
L 国有 n 个星球,还有 n−1 条双向航道,每条航道建立在两个星球之间,这 n−1 条航道连通了 L 国的所有星球。
小 P 掌管一家物流公司, 该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之间不会产生任何干扰。
为了鼓励科技创新, L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后,这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞, 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?
输入输出格式
输入格式:第一行包括两个正整数 n,m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n−1 行描述航道的建设情况,其中第 i 行包含三个整数 ai,bi 和 ti,表示第 i 条双向航道修建在 ai 与 bi两个星球之间,任意飞船驶过它所花费的时间为 ti。数据保证 1≤ai,bi≤n 且 0≤ti≤1000。
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j 个运输计划是从 uj 号星球飞往 vj号星球。数据保证 1≤ui,vi≤n
输出格式:一个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
输入输出样例
说明
所有测试数据的范围和特点如下表所示
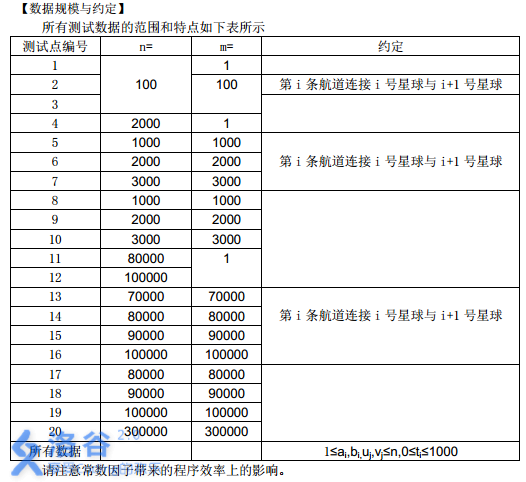
请注意常数因子带来的程序效率上的影响。
分析:因为是使所有路径中最大的那个最小,所以可以考虑二分答案。当二分一个答案mid后,统计所有路径长度大于mid的路径,再求出所有路径边的交集中,边长最大的那一个,再判断最长路径减去最大边长是否小于等于mid。以上过程可以通过树上差分来实现。

#include<bits/stdc++.h> #define N 300005 using namespace std; struct edge{int next,v,w;}; edge edg[N*2]; int head[N],now_edge=0; int grand[N][25]={0},gw[N][25]={0}; int depth[N],DEPTH; int dfsorder[N],c1=0; int edge_dfsorder[N]; void addedge(int a,int b,int w) { edg[now_edge]=(edge){head[a],b,w}; head[a]=now_edge++; edg[now_edge]=(edge){head[b],a,w}; head[b]=now_edge++; } void dfs(int x) { dfsorder[c1++]=x; for(int i=1;i<=DEPTH;i++) { grand[x][i]=grand[grand[x][i-1]][i-1]; gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1]; } for(int i=head[x];i!=-1;i=edg[i].next) { int to=edg[i].v; if(grand[x][0]==to)continue; depth[to]=depth[x]+1; grand[to][0]=x; gw[to][0]=edg[i].w; edge_dfsorder[c1]=i; dfs(to); } } void init(int n) { DEPTH=floor(log(n + 0.0) / log(2.0)); depth[1]=1; memset(grand,0,sizeof(grand)); memset(gw,0,sizeof(gw)); dfs(1); } int lca(int a,int b,int &c) { if(depth[a]>depth[b])swap(a,b); int ans=0; for(int i=DEPTH;i>=0;i--) if(depth[a]<depth[b]&&depth[grand[b][i]]>=depth[a]) ans+=gw[b][i],b=grand[b][i]; for(int i=DEPTH;i>=0;i--) if(grand[a][i]!=grand[b][i]) { ans+=gw[a][i]; ans+=gw[b][i]; a=grand[a][i]; b=grand[b][i]; } if(a!=b) { ans+=gw[a][0]; ans+=gw[b][0]; c=grand[a][0]; } else c=a; return ans; } int cf[N]={0}; int edge_Max=0; int cf_dfs(int tot) { for(int i=c1-1;i>=0;i--) { cf[grand[dfsorder[i]][0]]+=cf[dfsorder[i]]; if(cf[dfsorder[i]]==tot)edge_Max=max(edge_Max,edg[edge_dfsorder[i]].w); } } int from[N],to[N],Lca[N],ancestor[N]; void read(int &x) { int f=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} x*=f; } int main() { int n,m; memset(head,-1,sizeof(head)); //scanf("%d %d",&n,&m); read(n); read(m); for(int i=1;i<n;i++) { int a,b,c; //scanf("%d %d %d",&a,&b,&c); read(a); read(b); read(c); addedge(a,b,c); } init(n); int Left=0,Right=0,ans,road_Max,tot; for(int i=1;i<=m;i++) { // scanf("%d %d",&from[i],&to[i]); read(from[i]); read(to[i]); Lca[i]=lca(from[i],to[i],ancestor[i]); Right=max(Right,Lca[i]); } while(Left<=Right) { int mid=(Left+Right)/2; edge_Max=-1; road_Max=-1; tot=0; for(int i=1;i<=m;i++) { if(Lca[i]>mid) { road_Max=max(road_Max,Lca[i]); cf[from[i]]++; cf[to[i]]++; cf[ancestor[i]]-=2; tot++; } } if(road_Max==-1) { ans=mid; Right=mid-1; } else { cf_dfs(tot); if(road_Max-edge_Max<=mid) { ans=mid; Right=mid-1; } else Left=mid+1; } if(tot) { for(int i=1;i<=n;i++)cf[i]=0; } } printf("%d",ans); return 0; }
