JavaScript WebGL 矩阵

目录

• 引子
• 简介
• 单位矩阵
• 负矩阵
• 转置
• 基本运算
• 矩阵与向量相乘
• 二维变换
• WebGL 二维变换
• 参考资料

引子

本以为可以开始尝试三维的效果了，查了一下资料之后发现要先了解矩阵。在这里集中收集一下相关基础知识点。

• Origin
• My GitHub

简介

简单来说，矩阵（Matrix）是数字按行和列的矩形排列。一般描述先行后列，例如下面 2×3 矩阵：

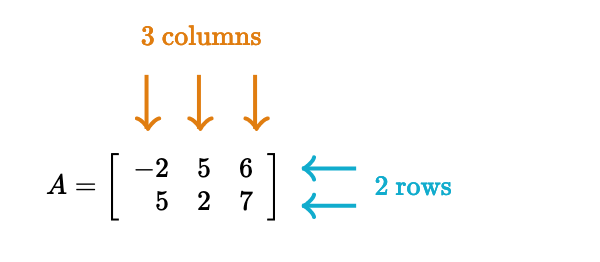
矩阵中每个元素表示也可以根据行和列标记，例如 a_1,2 表示第 1 行的第 2 列元素。

• 在应用数学学科中，矩阵常见于统计分析。
• 在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用。
• 计算机科学中，三维动画制作需要用到矩阵。

单位矩阵

单位矩阵有如下特点：

• 行数和列数相等。
• 对角线全是 1，其它全是 0 。
• 符号为大写字母 I 。
• 与任何矩阵相乘不会产生改变，例如 A × I = A。

下面是 3×3 单位矩阵：

负矩阵

简单来说就是矩阵里面每个元素求反。

例如矩阵 A 如下：

对应负矩阵就是：

转置

转置就是把矩阵的列和行对换。在右上角放一个 T 表示转置：

转置满足以下运算律：

• (A^T)^T = A
• (λA)^T = λA^T
• (AB)^T = A^TB^T

Back to top

基本运算

加法

只有同型（行数和列数对应相等）矩阵才能进行相加。相加时，对应的位置数进行相加。示例如下：

加法满足以下运算律：

• A + B = B + A
• (A + B) + C = A + (B + C)

减法

减法实际上就是与负矩阵相加。前提条件是两个为同型矩阵。示例如下：

矩阵与数相乘

矩阵与一个数相乘，矩阵中每个元素与数相乘。示例如下：

数乘满足以下运算律：

• λ(μA) = μ(λA)
• λ(μA) = (λμ)A
• (λ + μ)A = λA + λμ
• λ(A + B) = λA + λB

矩阵与矩阵相乘

两个矩阵能相乘的前置条件是：第一个矩阵的列数必须等于第二个矩阵的行数。

m×n 矩阵 A 乘以 n×p 矩阵 B 得到的是一个 m×p 矩阵 C 。矩阵 C 中每个元素的计算方式为：

这里有个结合实例的解释，下面是计算示例：

• c_1,1 = a_1,1 × b_1,1 + a_1,2 × b_2,1 + a_1,3 × b_3,1 = 0×1 + 1×2 + 2×3 = 8
• c_1,2 = a_1,1 × b_1,2 + a_1,2 × b_2,2 + a_1,3 × b_3,2 = 0×4 + 1×5 + 2×6 = 17
• c_2,1 = a_2,1 × b_1,1 + a_2,2 × b_2,1 + a_2,3 × b_3,1 = 2×1 + 1×2 + 0×3 = 4
• c_2,2 = a_2,1 × b_1,2 + a_2,2 × b_2,2 + a_2,3 × b_3,2 = 2×4 + 1×5 + 0×6 = 13

矩阵相乘满足以下运算律：

• (AB)C = A(BC)
• (A + B)C = AC + BC
• C(A + B) = CA + CB

这里需要注意矩阵相乘不满足互换律，也就是 AB != BA 。

逆矩阵

数有倒数，矩阵有类似的概念，叫逆矩阵，表示形式为 A^-1 。数与倒数的乘积为 1 ，类似的，矩阵与逆矩阵相乘结果是单位矩阵：AA^-1 = I 。

行数和列数相等的矩阵才可能有逆矩阵。更详细的讲解见这里。

计算逆矩阵的方式是：

• 用初等行运算
• 用余子式、代数余子式和伴随矩阵

这个在下面除法中会用到。

矩阵与矩阵相除

在矩阵中是没有除的概念，乘以逆矩阵，这和除是相同的效果。

假设已知矩阵 A 和 B ，且 A 存在逆矩阵，需要求矩阵 X ：

XA = B

可以这样做：

• XAA^-1 = BA^-1

前面有提到 AA^-1 = I，所以：

• XI = BA^-1

单位矩阵相乘是不会改变原矩阵的，所以：

• X = BA^-1

矩阵与向量相乘

矩阵与向量相乘是方程组的一种解释方式，具体解释看这里，有两条重要的规律：

• 矩阵乘以右侧列向量可看成矩阵各列向量的线性组合，结果为列向量。
• 左侧行向量乘以矩阵可看成矩阵各行向量的线性组合，结果为行向量。

WebGL 中的顶点坐标都可以转换为向量的形式，进行变换时，向量和矩阵相乘是一种高效的方式。先看看二维变换：位移、缩放和旋转。

Back to top

二维变换

以下是纯数学理论计算，跟实际编程应用可能有些出入。

位移

先看下不使用矩阵的实现方式，坐标(x, y)，分量对应位移 T_x 和 T_y，那么新坐标：

• newX = x + T_x
• newY = y + T_y

单位矩阵通常是生成其它变换矩阵的起点，向量与单位矩阵相乘不会改变向量：

两种计算方式对比：

• 非矩阵方式：newX = x + T_x
• 矩阵方式：newX = x

发现用 2×2 矩阵变换不行，需要 3×3 矩阵 。向量也要多一个分量才能相乘，这里设置为 z ，再来看下计算：

可以发现当 z = 1 时得到的结果就符合了位移效果。

缩放

缩放量为 S_x 和 S_y ，2×2 矩阵就可以满足缩放的效果：

旋转

先看下不使用矩阵的实现方式。为了描述旋转，需要指明：

• 旋转轴
• 旋转方向
• 旋转角度

这里设定旋转绕 Z 轴，旋转方向是逆时针，旋转角度是 β 。点 (x, y) 旋转 β 角度后变成了点(newX, newY)，结合三角函数可得：

• newX = xcos(β) - ysin(β)
• newY = xsin(β) + ycos(β)

再看下使用矩阵的实现方式：

两种计算方式对比：

• 非矩阵方式：newX = xcos(β) - ysin(β)
• 矩阵方式：newX = ax + by

如果 a = cos(β)，b = -sin(β)，两个等式就相同了。类似的对 y 坐标转换后，最终得到的矩阵为：

WebGL 二维变换

在数学约定中，横着是行，竖着是列，基于这样进行构造矩阵。但在 WebGL 编程中，由于一些原因，程序会把视觉上的行解析为列。

位移

这是数学意义的位移矩阵形式：

const m3 = [
  1,  0,  tx, // 行
  0,  1,  ty, // 行
  0,  0,  1,  // 行
]

这是在 WebGL 编程中能正确解析的位移矩阵：

const m3 = [
  1,  0,  0, // 列
  0,  1,  0, // 列
  tx, ty, 1, // 列
]

来分别看看这两个位移矩阵的示例：

• 编程使用 WebGL 角度位移矩阵示例
• 编程使用数学角度位移矩阵示例

程序中使用数学角度的矩阵形式，对应数学角度上会导致计算结果都到 Z 分量上了，二维是用不到 Z 分量的，不会产生任何变化，示例也是这样的结果。

缩放

WebGL 中缩放矩阵：

function getTransform (x, y) {
  return [
    x, 0, 0,
    0, y, 0,
    0, 0, 1,
  ];
}

这是示例。

旋转

WebGL 中旋转矩阵：

function getTransform (angle) {
  const radian = (Math.PI * angle) / 180;
  const cosA = Math.cos(radian);
  const sinA = Math.sin(radian);
  return [
    cosA, sinA, 0,
    -sinA, cosA, 0,
    0, 0, 1,
  ];
}

这是示例。

Back to top

参考资料

• 矩阵百科
• 矩阵
• WebGL 二维矩阵