问题描述:
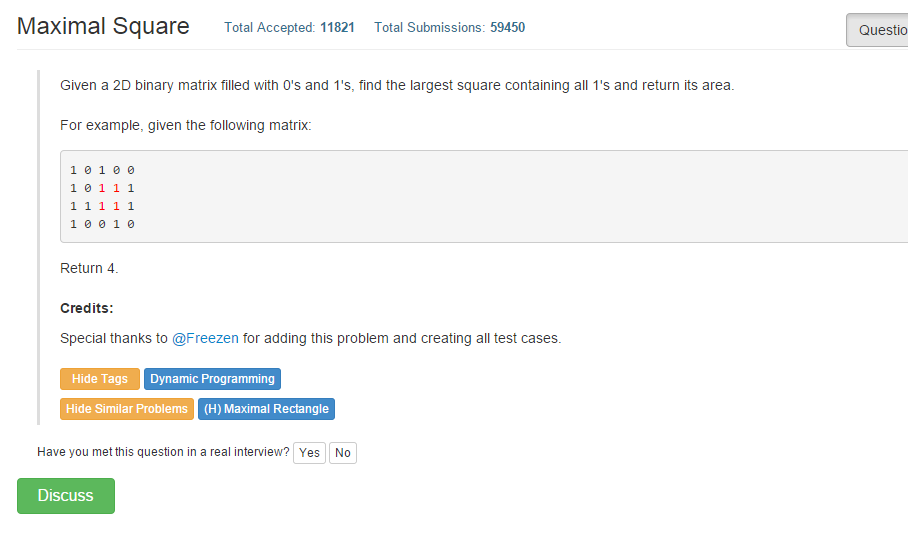
题目链接: 221 Maximal Square
问题找解决的是给出一个M*N的矩阵, 只有'1', '0',两种元素; 需要你从中找出 由'1'组成的最大正方形。恩, 就是这样。
我们看到, 这道题目的标签还是DP, 那么问题的关键就是要找到一个符合判断是否为正方形的递推式。
老套路, 先看基本型 , 对于一个2*2的正方形,对于右下角的元素(1,1)而言, 他的上(0,1), 左(1,0), 左上(0,0)三个元素应该都是'1',
, 对于一个2*2的正方形,对于右下角的元素(1,1)而言, 他的上(0,1), 左(1,0), 左上(0,0)三个元素应该都是'1',
如此才能够组成一个合规的正方形; 那么如果是一个3*3呢, 首先他必然是一个2*2, 然后左加一列,上添一行,就由一个2*2成了一个3*3型,所以, 对于在矩阵中的
任意一个点'1'只要不断匹配他的左边列和上边行都是‘1’, 并计数后再往外匹配一层,知道出现'0'或者到达边界即可, 然后从每个点中选出匹配到的最大层数, done!
基本套路就是如此, 但是每个点都走一遍就是M*N个点, 后每个点都再外面一层逐个匹配, 时间复杂度消耗不起,O(M^2*N^2), 一般考虑M*N,直接近似4次方的复杂度,
肯定不可取。既然从后往前不靠谱, 那我们从前往后推又如何呢?
除去边界(即第一行与第一列),对于任意一个matrix[i][i],他所处的方形应该前一层决定:左边(matrix[i][j-1]), 上边(matrix[i-1][j]),左上(matrix[i-1][j-1])决定,
同样的, 我们也需要一个结果矩阵 ret[M][N] 记录每个对应点所处的方形层数。
再看最基本型: 对于在matrix[1][1]出的点, 他的左上外层全为'1', 故这个点在ret[1][1]就+1,结果记为2,
对于在matrix[1][1]出的点, 他的左上外层全为'1', 故这个点在ret[1][1]就+1,结果记为2,
即:if: (top != '0', left!='0', top_left!='0')
then: ret[i][j] = matrix[i][j]+1;
在考虑到这一步的时候, 觉得已经ok了, 立刻在页面写好代码提交, 结果却是一个大大的Wrong Answer! 当下觉得没错啊, 对于每个点是不是处于方形都做了
判断, 而且判定了之后还把层数+1嘞,于是输出结果矩阵一看:
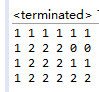
很明显, 对于层数计算, 并没有获取前一层的都处于的方形层数, 要知道,假设在[i][j]为止是属于3*3的方形, 那么必然有点[i-1][j],[i][j-1], [i-1][j-1]这3个都至少属于
2*2的方形, 可能用图示更清楚:
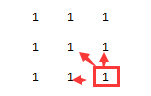 left:
left: top:
top: left_top:
left_top:
所以上面的情形如果在递推产生的ret矩阵中就是这个样子:
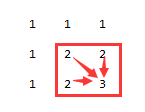 left:
left: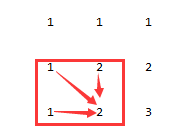 top:
top: left_top:
left_top:
所以, 更正后的递推式应该是:

再次提交, Accepted!
最后只解决的代码:

另外, 还有一道相近的 (链接在这里), 这次不定形状了, 你是一行, 还是正方形没有限制了, 难度也提升为Hard级别,
(链接在这里), 这次不定形状了, 你是一行, 还是正方形没有限制了, 难度也提升为Hard级别,
但核心思想肯定没变, 各位额可以尝试下, 此题明后日贴个人解决思路。
最后还是老话, 本人贴上来的解法和思路仅作是记录,或者还可以向各位看官交流学习,有帮助就好。