洛谷P1155 双栈排序

P1155 双栈排序

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

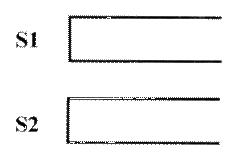
操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1，2，…，(n-1)，n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

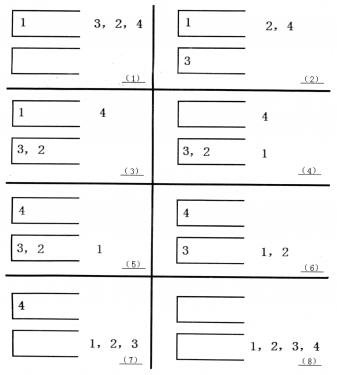
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入输出格式

输入格式：

输入文件twostack.in的第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1~n的排列。

输出格式：

输出文件twostack.out共一行，如果输入的排列不是“可双栈排序排列”，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入样例#1：

【输入样例1】
4
1 3 2 4
【输入样例2】
4
2 3 4 1
【输入样例3】
3
2 3 1

输出样例#1：

【输出样例1】
a b a a b b a b
【输出样例2】
0
【输出样例3】
a c a b b d

说明

30%的数据满足： n<=10

50%的数据满足： n<=50

100%的数据满足： n<=1000

/*
    二分图染色+模拟 
    
    1.首先考虑一个简单情况——单栈排序,显然有这样的一个事实： 
    a[i]和a[j] 不能压入同一个栈?存在一个k,使得i < j < k且a[k] < a[i] < a[j] 
    时间复杂度为O(n^3).对于n<=1000仍显吃力,对此可以用动态规划的思想,将上述复杂度降到O(n^2)。 
    状态:f[i]=min(a[i],a[i+1], … ,a[n]) 
    边界条件:f[n+1]=INF; 
    状态转移方程:f[i]=min(f[i+1],a[i]); 
    于是上述判断就转化为了f[j+1] < a[i] && a[i] < a[j] 
    
    2.扩展到双栈排序: 
    如果a[i]和a[j]不能在一个栈内，即连接一条i与j之间的无向边,接下来我们只需要判断这个图是否为二分图 
    由于题目中说编号的字典序要尽可能的小，那么就把编号小的尽可能放到stack1 
    判断二分图的方法可以采用黑白染色的方式，先从编号小的开始染,第一个顶点染成黑色,相邻的顶点染成不同的颜色,如果发现黑白冲突,那么说明这个图不是一个二分图,是不合法的,输出0. 
    (DFS或BFS染色均可) 
    3.染色后所有黑色的点进stack1,所有白色的点进stack2，最后模拟输出过程就可以了.
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 1001
using namespace std;
int a[maxn],v[maxn],f[maxn];
int q1[maxn],top1,q2[maxn],top2,now,l;
bool ok[maxn][maxn];
int n;
void dfs(int x,int y){
    v[x]=y;
    for(int i=1;i<=n;i++)
        if(ok[i][x]){
            if(v[i]==y){puts("0");exit(0);}
            else if(v[i]==0)dfs(i,y^1);
        }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    f[n+1]=n+1;
    for(int i=n;i>=1;i--)f[i]=min(f[i+1],a[i]);
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            if(a[i]<a[j]&&a[i]>f[j])ok[i][j]=ok[j][i]=1;
    for(int i=1;i<=n;i++)if(v[i]==0)dfs(i,2);
    l=1;now=1;a[0]=n+1;
    while(now<=n){
        if(v[l]==2&&a[q1[top1]]>a[l])printf("a "),q1[++top1]=l++;
        else if(now==a[q1[top1]])printf("b "),top1--,now++;
        else if(v[l]==3&&a[q2[top2]]>a[l])printf("c "),q2[++top2]=l++;
        else if(now==a[q2[top2]])printf("d "),top2--,now++;
    }
}