2017-10-19 NOIP模拟赛

Count（哈格朗日插值）

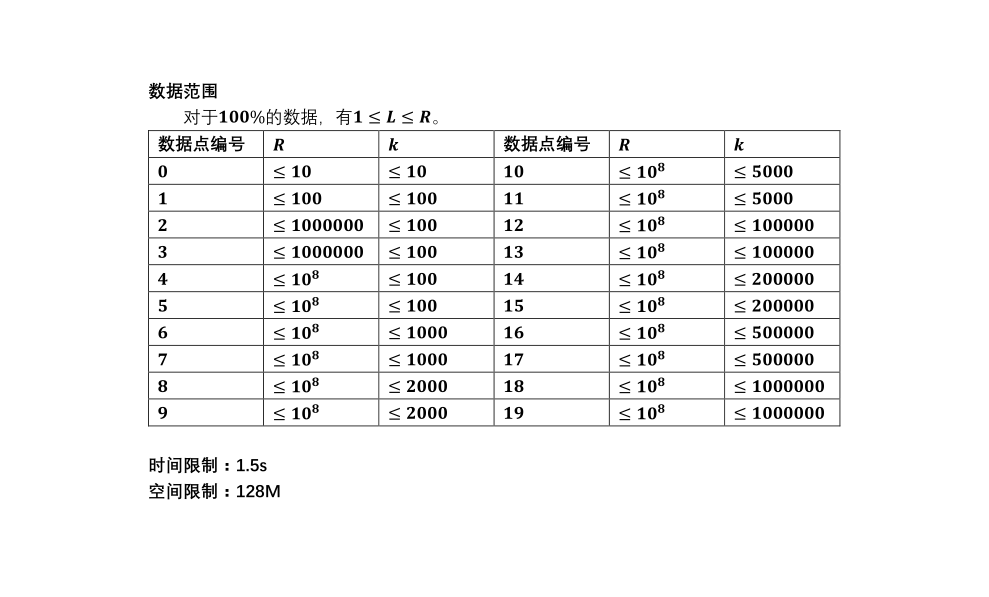
题解: 有个定理，另sum(x)表示小于等于x的数中与x互质的数的和

sum(x)=φ(x)*x/2    最后可知f(x)=x  （f(1)=2）  当然打表能知道。

然后就转化为了求Σi^k

然后就是拉格朗日插值法了，不在我理解范畴........

但这个博客介绍挺好哒 http://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html

#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 998244353
#ifdef WIN32
#define PLL "%I64d"
#else
#define PLL "%lld"
#endif
using namespace std;
int l,r,k;
long long ans;
long long mul(long long a,long long b){
    long long res=0;
    while(b){
        if(b&1)res=res+a;
        a=a+a;
        if(res>=mod)res-=mod;
        if(a>=mod)a-=mod;
        b>>=1;
    }
    return res;
}
long long Pow(long long a,int b){
    long long res=1;
    while(b){
        if(b&1)res=mul(res,a);
        a=mul(a,a);
        b>>=1;
    }
    return res;
}
int main(){
    freopen("count.in","r",stdin);freopen("count.out","w",stdout);
    //freopen("Cola.txt","r",stdin);
    scanf("%d%d%d",&l,&r,&k);
    for(int i=l;i<=r;i++){
        if(i==1)ans+=Pow(2,k);
        else ans+=Pow(i,k);
        if(ans>=mod)ans-=mod;
    }
    printf(PLL,ans);
    //cout<<ans;
}

Block

/* 
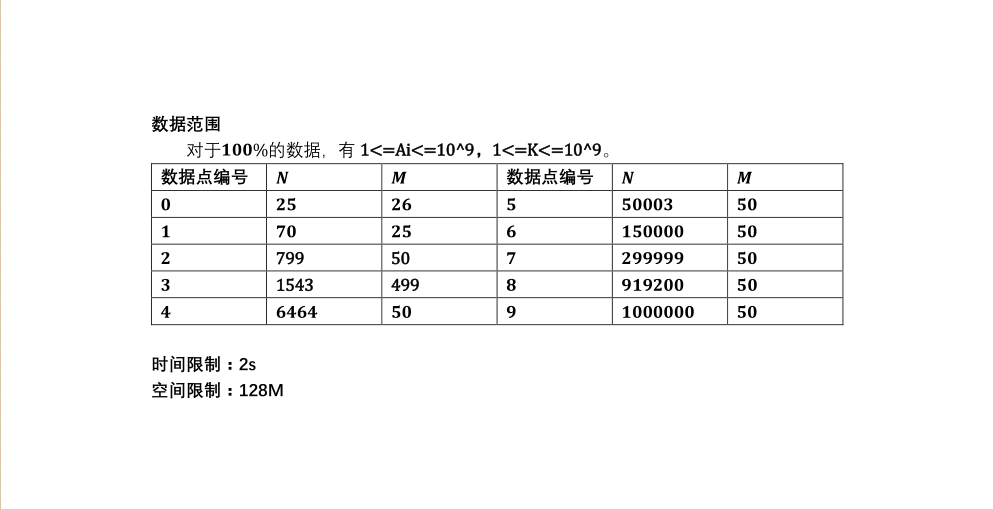
    题意转化为求最大的区间长度使得这段区间和减k>=0 
    首先做前缀和，可知若当前到了k,i<j<k && sum[i]<sum[j]则j一定不可能比i更优 
    用单调栈维护这个过程。然后倒序更新答案即可。 
*/ 

#include<iostream>
#include<cstdio>
#include<cstring>

#define N 1000007

using namespace std;
long long sum[N];
int a[N],st[N],top,n,m,cnt;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void solve(int k)
{
    top=1;int res=0;
    for(int i=1;i<=n;i++) 
    {
        sum[i]=sum[i-1]+a[i]-k;
        if(!top || sum[st[top]]>sum[i]) st[++top]=i;
    }
    for(int i=n;i>=1;i--) 
    {
        while(top && sum[i]>=sum[st[top]]) top--;
        res=max(res,i-st[top+1]);
    }
    printf("%d ",res);
}

int main()
{
    freopen("blocks.in","r",stdin);
    freopen("blocks.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    while(m--) solve(read());
    return 0;
}

Biology（Trie树+lca）

#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 1000010
#define root 1
using namespace std;
int n,m,tr[maxn][26],num,id[150010],tc=1,fa[maxn],dep[maxn];
char s[10010];
void Insert(){
    int now=root;
    for(int i=strlen(s+1);i>=1;i--){
        int p=s[i]-'a';
        if(tr[now][p]==0){
            tr[now][p]=++tc;
            fa[tc]=now;
            dep[tc]=dep[now]+1;
        }
        now=tr[now][p];
    }
    id[num]=now;
}
int lca(int a,int b){
    while(a!=b){
        if(dep[a]<dep[b])swap(a,b);
        a=fa[a];
    }
    return a;
}
int main(){
    freopen("biology.in","r",stdin);freopen("biology.out","w",stdout);
    //freopen("Cola.in","r",stdin);
    scanf("%d%d",&n,&m);
    fa[1]=0;dep[1]=0;
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        num=i,Insert();
    }
    int op,nn,x;
    for(int i=1;i<=m;i++){
        scanf("%d",&op);
        if(op==1){
            scanf("%s",s+1);
            num++;
            Insert();
        }
        else{
            scanf("%d",&nn);
            int now;
            for(int j=1;j<=nn;j++){
                scanf("%d",&x);
                if(j==1)now=id[x];
                else now=lca(now,id[x]);
            }
            printf("%d
",dep[now]);
        }
    }
    /*int sz=sizeof(tr)+sizeof(id)+sizeof(fa)+sizeof(dep);
    cout<<sz/1048576;*/
    return 0;
}
/*
5 5
zzj
pri
prime
ime
owaski
2 3 1 3 5
2 2 2 3
1 actri
2 2 3 4
2 3 2 6 5
*/

#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 1000010
#define root 1
using namespace std;
int n,m,tr[maxn][26],num,id[150010],tc=1,fa[maxn][20],dep[maxn];
char s[10010];
void Insert(){
    int now=root;
    for(int i=strlen(s+1);i>=1;i--){
        int p=s[i]-'a';
        if(tr[now][p]==0){
            tr[now][p]=++tc;
            dep[tc]=dep[now]+1;
            fa[tc][0]=now;
            for(int j=1;j<=18;j++)fa[tc][j]=fa[fa[tc][j-1]][j-1];
        }
        now=tr[now][p];
    }
    id[num]=now;
    //for(int i=1;i<=18;i++)fa[now][i]=fa[fa[now][i-1]][i-1];
}
int lca(int a,int b){
    if(dep[a]<dep[b])swap(a,b);
    for(int i=18;i>=0;i--)
        if(dep[fa[a][i]]>=dep[b])a=fa[a][i];
    for(int i=18;i>=0;i--)
        if(fa[a][i]!=fa[b][i])
            a=fa[a][i],b=fa[b][i];
    if(a==b)return a;
    return fa[a][0];
}
int main(){
    freopen("biology.in","r",stdin);freopen("biology.out","w",stdout);
    //freopen("Cola.txt","r",stdin);
    scanf("%d%d",&n,&m);
    fa[1][0]=0;dep[1]=0;
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        num=i,Insert();
    }
    int op,nn,x;
    for(int i=1;i<=m;i++){
        scanf("%d",&op);
        if(op==1){
            scanf("%s",s+1);
            num++;
            Insert();
        }
        else{
            scanf("%d",&nn);
            int now;
            for(int j=1;j<=nn;j++){
                scanf("%d",&x);
                if(j==1)now=id[x];
                else now=lca(now,id[x]);
            }
            printf("%d
",dep[now]);
        }
    }
    /*int sz=sizeof(tr)+sizeof(id)+sizeof(fa)+sizeof(dep);
    cout<<sz/1048576;*/
    return 0;
}
/*
5 5
zzj
pri
prime
ime
owaski
2 3 1 3 5
2 2 2 3
1 actri
2 2 3 4
2 3 2 6 5
*/