题目描述
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场,分别位于一个矩形的四个顶点上,同一个城市中两个机场之间有一条笔直的高速铁路,第I个城市中高速铁路了的单位里程价格为Ti,任意两个不同城市的机场之间均有航线,所有航线单位里程的价格均为t。
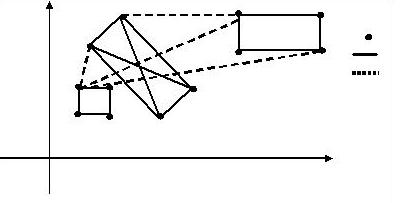
图例(从上而下)
机场 高速铁路
飞机航线
注意:图中并没有
标出所有的铁路与航线。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
输入输出格式
输入格式:第一行为一个正整数n(0<=n<=10),表示有n组测试数据。
每组的第一行有四个正整数s,t,A,B。
S(0<S<=100)表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,(1<=A,B<=S)。
接下来有S行,其中第I行均有7个正整数xi1,yi1,xi2,yi2,xi3,yi3,Ti,这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第I个城市中任意三个机场的坐标,T I为第I个城市高速铁路单位里程的价格。
输出格式:共有n行,每行一个数据对应测试数据。 保留一位小数
输入输出样例
输入样例#1:
1 3 10 1 3 1 1 1 3 3 1 30 2 5 7 4 5 2 1 8 6 8 8 11 6 3
输出样例#1:
47.5
思路:
对于每一个城市四个顶点处的机场,把它编号为4*i-3, 4*i-2, 4*i-1, 4*i,输入的数据只包括前三个点,而要求出所有机场两两之间的最小花费,必须先求出第四个机场的坐标
矩形是大家喜闻乐见的图形,众所周知,矩形中任意三点可围成一个直角三角形,那么第四个点就是直角顶点关于斜边的对应点(不是对称点)
于是问题又指向找出斜边
学过平面几何的孩子大概都知道两点间距离公式,和直角三角形三边关系
用两点间距离公式求出直角三角形的每一条边,两两比较,最长的一条边自然就是斜边,不是这条边端点的那个点就是第四个点的对应点
来一个图,看看知道斜边和对应点,第四个点该怎么求

容易知道,两个蓝色的三角形是全等的
所以ED==FC,AE==BF
进而得知x[C]=x[B]+x[D]-x[A],y[C]=y[B]+y[D]-y[A]
现在,第四个点坐标求出来了,开始处理每一条边
同一个城市内的则用高速铁路单价
不同城市的用飞机单价
找到每两个飞机场之间的费用后
跑一遍floyd
分别试试A,B两城市的四个机场,选费用最小的一条路,保留一位小数输出
代码
#include<iostream> #include<cmath> #include<cstdio> #include<cstring> using namespace std; int fee[1000],s,t,A,B,x[1000],y[1000];//x[],y[]某个机场的横纵坐标 double my[1000][1000],ans; void find_fee(int one,int two){ my[one][two]=sqrt((x[one]-x[two])*(x[one]-x[two])+(y[one]-y[two])*(y[one]-y[two])); //两点间距离公式 //cout<<my[one][two]<<endl; if(((one-1)/4)==((two-1)/4))my[one][two]*=fee[(one-1)/4+1]; else my[one][two]*=t; my[two][one]=my[one][two]; } int find_xie(int one,int two,int three){ if(my[one][two]>my[two][three]&&my[one][two]>my[one][three])return three; if(my[two][three]>my[one][two]&&my[two][three]>my[one][three])return one; if(my[one][three]>my[two][three]&&my[one][three]>my[one][two])return two; } void find_forth(int one,int two,int three){ find_fee(one,two); find_fee(two,three); find_fee(one,three); int forth=find_xie(one,two,three); if(forth==one){ x[three+1]=x[two]+x[three]-x[one]; y[three+1]=y[two]+y[three]-y[one]; } if(forth==two){ x[three+1]=x[one]+x[three]-x[two]; y[three+1]=y[one]+y[three]-y[two]; } if(forth==three){ x[three+1]=x[two]+x[one]-x[three]; y[three+1]=y[two]+y[one]-y[three]; } } double Min(double xx,double yy){ return xx<yy; } int main(){ //freopen("jh.txt","w",stdout); int T;cin>>T; while(T--){ ans=0x7fffffff; cin>>s>>t>>A>>B; memset(my,127/3,sizeof(my)); memset(x,0,sizeof(x)); memset(y,0,sizeof(y)); memset(fee,0,sizeof(fee)); for(int i=1;i<=s;i++){ cin>>x[4*i-3]>>y[4*i-3]>>x[4*i-2]>>y[4*i-2]>>x[4*i-1]>>y[4*i-1]>>fee[i]; find_forth(4*i-3,4*i-2,4*i-1); } for(int i=1;i<=4*s;i++) for(int j=1;j<=4*s;j++) find_fee(i,j); for(int k=1;k<=4*s;k++) for(int i=1;i<=4*s;i++) for(int j=1;j<=4*s;j++){ if(i!=j&&i!=k&&k!=j){ if(my[i][k]+my[k][j]<my[i][j]) my[i][j]=my[i][k]+my[k][j]; } } for(int i=4*A;i>=4*A-3;i--){ for(int j=4*B;j>=4*B-3;j--){ if(ans>my[i][j]) ans=my[i][j]; } } printf("%.1f ",ans); } }