前面学习了TSP和Dijkstra动态规划的问题,核心思想是从目前的节点出发找下一个最短的路径(这两种算法刚好相反,一个从起点开始,一个从“终点”开始),和人生的发展路径何其相似;除了发展路径的选择,人的一生还面临另一个棘手的问题:试错!人生初落地,什么都不懂,大部分知识都是后天一点一滴学习得来的。除了极个别智商超群的天才(比例估计不到万分之一),大部分普通人都会犯各种错误,从错误中吸取经验教训,重头再来的时候改正上次犯的错(业界正式的称呼为“回溯”);和这种思路类似的还有另一个经典的算法——8皇后(扩展一下就是N皇后)!
8皇后的规则:棋盘式8*8的正方格子,必须放置8个皇后的棋子;限制条件为:每行、每列、每个斜线只能有一个皇后(或则说任意两个皇后之间不能相邻挨着,也不能出现在同一条斜线)!如下这种方式是可以的,该怎么找出所有的摆放方法了?
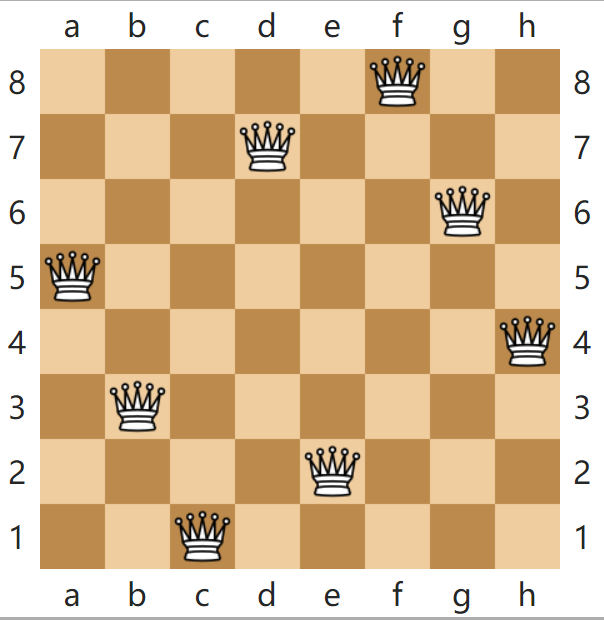
为了突出解决问题的思路,这里把8皇后的问题简化成4皇后,其他规则不变;既然有4个皇后,就挨个在棋盘上尝试,看看会不会出错;如果错了,就退回上一步重来,具体的过程如下:
(1)现在刚开始,整个棋盘都是空的,没有任何头绪,只能从第一个格子(当然也可以随机选其他格子尝试,只要符合规则就行)开始尝试,放一个皇后;为了满足游戏规则,把不能放皇后的格子都标识成1,后续直接跳过这些格子,如下:
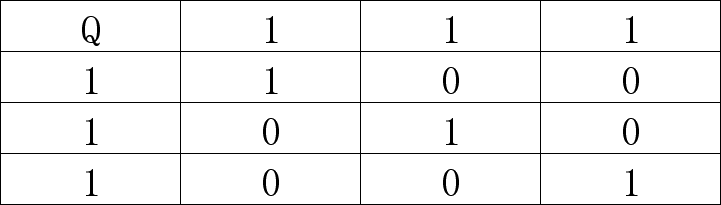
(2)Q和1的格子不能再用了,继续选择0的格子放皇后。这里随机选择2行3列的格子放皇后,同样把同行、同列、同斜线(注意别忘记这个)的格子都置1,结果如下:
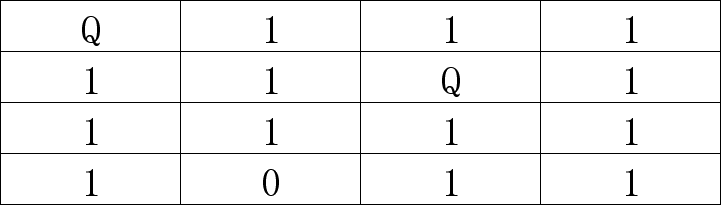
(3)此时整个棋盘只剩第4行还有0,第三行已经全军覆没,没法再放皇后了,说明第二部显然是错了,这里就应该回溯纠错,退回到(1)重新开始。既然皇后不能放2行3列,那就放2行4列试试呗,结果如下:
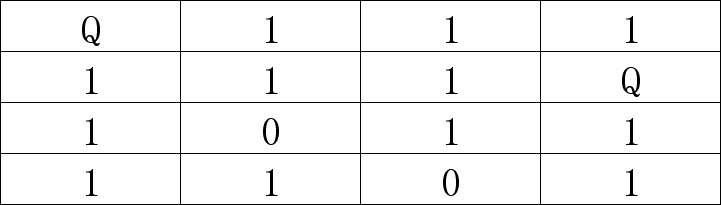
(4) 目前来看没毛病,第3行、4行还有0可以放。继续把第3行的0放上皇后,结果如下:
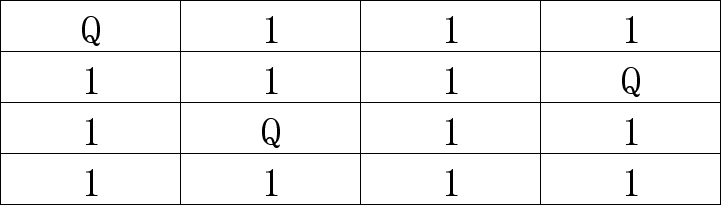
(5)非常不幸的是第4行没位置了,说明(3)也是错的,要回到(2);但是(2)刚才已经证明是错的,只能回到(1);这里是从1行1列开始的,通过(2)-(4)已经证明是不行的,只能换个地方继续。比如从1行2列开始,如下:
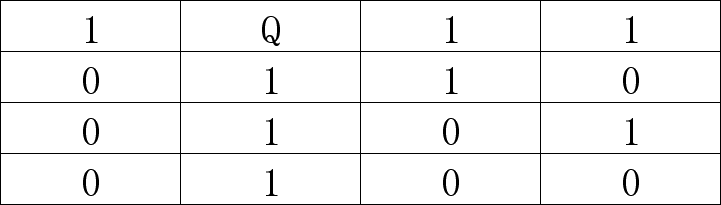
(6)此时第2行1列、4列都能放皇后,随机选择1列放皇后,如下:目前来看没毛病,继续;
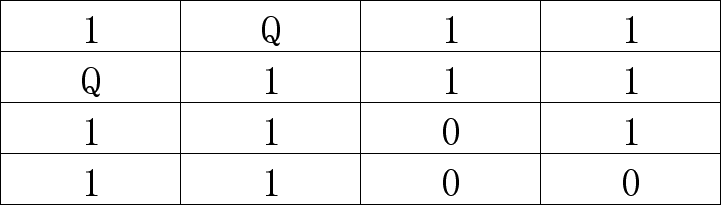
(7)第3行只是第3列了,放个皇后发现第4行没位置了,说明(6)是错的,要回溯到第5步:
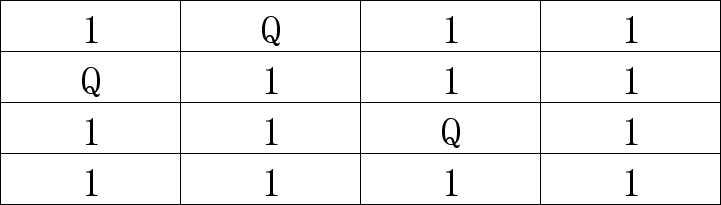
(8) 第(5)步是在2行1列放的皇后,通过(6)、(7)两部已经证明是错的了,只能在2行4列放皇后,结果如下:
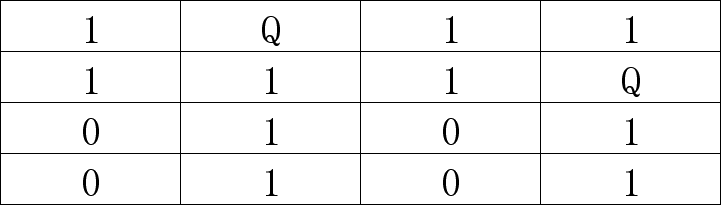
(9) 目前来看也没毛病,第3行有两个位置可以放皇后;这里不用再尝试了,一眼就能看出来两个位置都行,也就是如下两种结果:
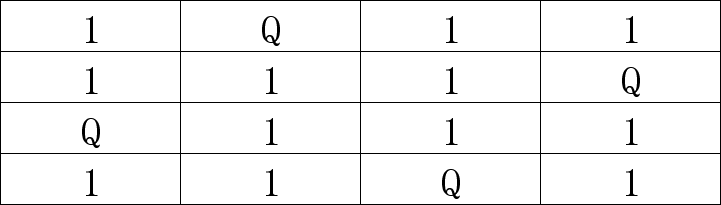
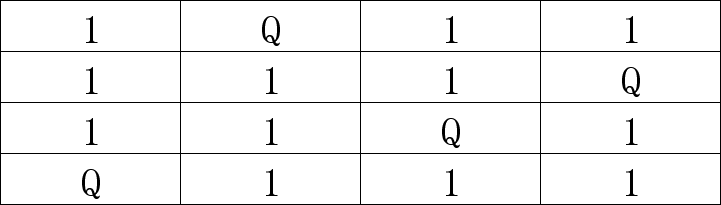
整个过程就是如此,目前找到了2种摆放的方法,但实际上4皇后是不是只有这2种解法了?我不确定,感兴趣的小伙伴可以尝试从1行3列开始摆放再试试!
核心思路也很简单,即:
- 刚开始不知道从那开始,只能随机选个位置
- 每次摆放皇后后如果发现出错,退回到上一步重新换个地继续摆放皇后
- 重复上面的步骤,直到所有的皇后都摆放完毕
本质行就是利用计算机快速的算力不断试错,不断纠错,最终达到业务目的!
参考:1、https://zh.wikipedia.org/wiki/%E5%85%AB%E7%9A%87%E5%90%8E%E9%97%AE%E9%A2%98 八皇后问题