年底了,在做各种总结,回顾一下2020年的收获和不足。这一年开了博客,总结了逆向、渗透和网络安全方面的技术和知识点,距离自己设定的目标又进了一步;总结的时候突然想到了一个经典的路径规划问题:一个旅行者从A出发到F,中间有多条路线走,哪条路线是成本最低的了? 这个和人生职业发展是不是类似了?小时候立志成为xxx,为了实现理想,可能要分多步走,怎么规划才能成本最低、效果最优了?PS: 路由器的OSPF路径规划也用了这种算法!
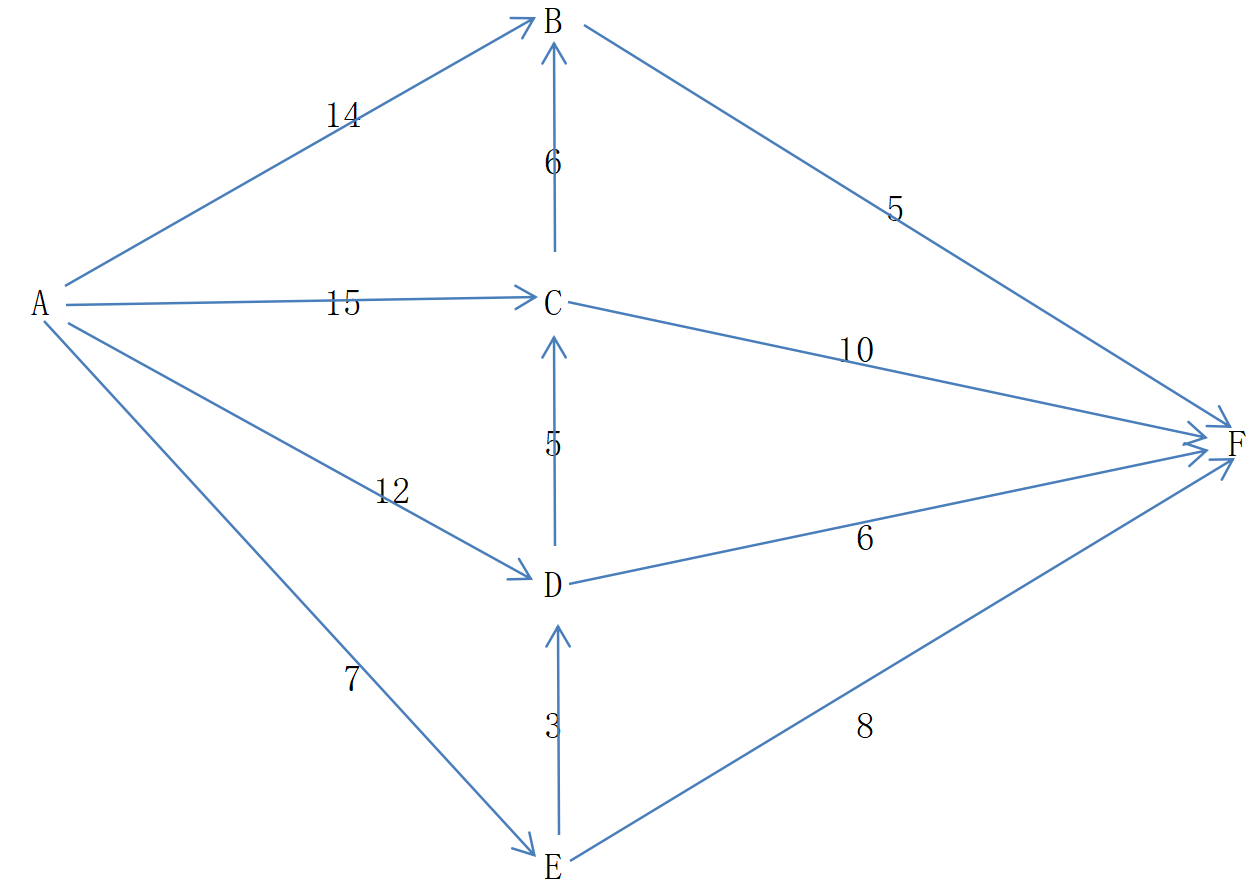
1、下面是示意图: 起点是A,终点是F,中间点是BCDE,每连个点之间都是通的,路径的长度如图所示,从A到F那条路才是最短的(注意:数字是随机生成的,并不和看起来的长度成正比)?这就是业界著名的Dijkstra动态规划问题;
解决问题的核心思路:
- 既然要找到全局最短的路径,那么必须找到每一步的最短路径,所有步骤加起来才会是全局最短的;
- 从A出发,穷举连接所有节点的距离,选出最短的节点,下一步从该节点继续重复这一步,直到到达终点;
上面是理论思路,下面具体的步骤:
(1)从A出发,穷举和A连接所有节点的距离。如果没直连,距离用NA或无穷大表示,如下:

从A出发,到E的距离最短,此时锁定E节点,将其作为跳板继续寻找下一条最优的路线,具体的方法:E直连了D和F,距离分别是3和8,那么A如果以E为中继节点,到D和F的距离就变成了7+3=10、7+8=15;如果A不以E为中继节点,到D和F的距离分别是12和无穷大,很显然通过E中继比之前的距离更短,这里就更新路由表如下:

因为已经使用了E作为中继,就不能再动,这里用黄色标记一下;同时把AD和AF截至目前的最短路径(分别是AED、AEF)也标记一下;至此,已经找到了第一个最优的中继节点E:通过该节点中继能缩短现有其他路线的距离(这里缩短了A->D和A->F的距离)!
(2)跟新后的路由表如上:此时继续选距离最短的点中继。相比之下,AED距离10是最短的,所以从这里D开始中继;和D直连的节点是C和F,如果以D为中继节点,A到C和F的距离分别是10+5=15、10+6=16,和以前比,AC的距离没变,AF的距离比之前的15还要多1,所以从D出发,并没有缩短现有路由表的距离,此时忽略D节点中转,路由表标时如下:

(3)继续寻找下一个可能的最优中继节点:先在只剩B和C了,相比之下AB距离14,那么临时把B作为中继节点;B只能到F,那么ABF就是14+5=19,还是比现有的AEF大,所以B节点继续忽略;

(4)先在只剩C节点了: C能到B和F,ACB=21、ACF=25,和现在的AB、AF比并没有降低,所以不用更新现有路由表;这一步后所有的中间节点都已经遍历,从A到各个节点最优的路由也就定了,如下:

A到B、C不变,到D和F从E中转!
2、和Dijkstra动态规划类似的另一个问题:TSP(traveling salesman problem),一个salesman要遍历所有城市,但每座城市只能去一次,最后回到起点;城市之间互相都是通的,但来去的成本不同,要求遍历所有城市的成本最低;抽象出来的问题描述如下:
A、B、C、D四座城市互相连通(双向联通),城市之间的travle成本如右边矩阵所示;这个矩阵是非对称矩阵,具体到业务上就是来回的成本不是一样的。比如从A->B是16,但是从B->A是8;又比如C->D是9,但D->C是2;从那个城市出发,这个城市就从行查目的地的城市放在列!
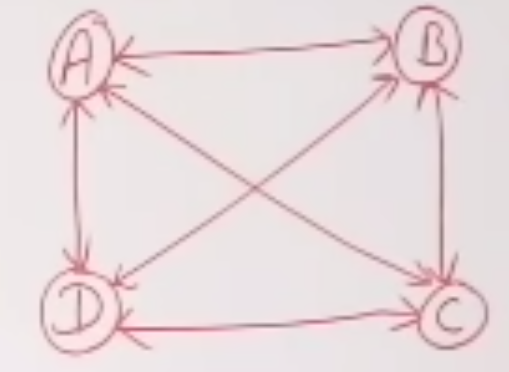

不同于上面的Dijkstra路由规划,这里的TSP是双向的,最核心的区别在于:TSP要求回到出发点,而Dijkstra不需要;前者要求回路闭环,后者要求单向无环!正是这种差异,导致了算法层面刚好相反:Dijkstra是从起点出发(刚开始不知道从哪跳转,只能从起点开始选下一个中继点),每次都找最近的节点作为中继;TSP是知道“终点”,所以从所有能穷举的“终点”出发,倒过来找成本最低的边;
具体的过程如下:
(1)先穷举(这就是这种算法复杂度高的原因之一:如果)出所有从A出发、最终能回到A的路线,如下:
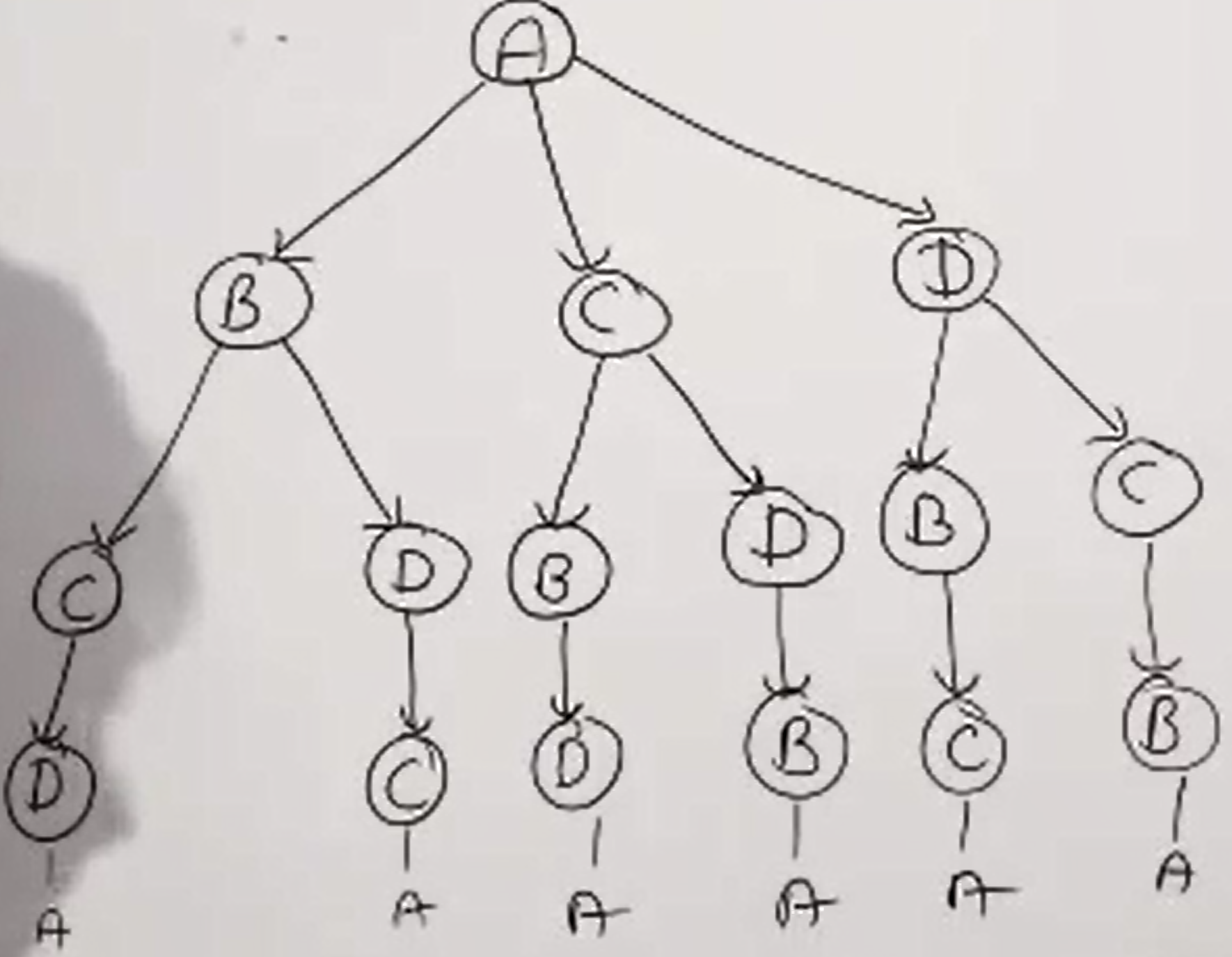
(2)根据上面的那个遍历矩阵,从底部的“终点”出发,计算出每个分支的遍历成本,选择成本最小的分支替代替另一个分支,比如:
- 最左边的分支:BCDA和BDCA,这两个分支只能留一个,就看那个分支的成本最低了;BCDA的成本是13+9+5=27,BDCA的成本是16+2+4=22,比前面的小,所以BCDA废除,这里只保留BDCA;
- 同理:中间的C分支有CBDA和CDBA,成本分别是7+16+5=28和9+12+8=29,保留CBDA,废除CDBA;
- 同理:最右边的分支DBCA和DCBA,成本分别是12+13+4=29和2+7+8=17,保留DCBA;
- B、C、D三个分支中,B分支最短是22,是BDCA;C分支最短是28,是CBDA;D分支最短是17,是DCBA;
- AB=16,加上BDCA的22,最终是38;AC=11,加上CBDA的28,最终是39;AD=6,加上DCBA的17,最终是23;所以ADCBA是最优的路径,成本是17,完胜!
(3)为了便于编码实现,还需要进一步抽象整个过程,如下:
- g(i,s) = min{w(i,j)+g(j,{s-j})}, 其中i、j是图中的点,s是去掉出发点后所有点的集合;w(i,j)表示图中i、j两个点之间的权重;s-j表示除去j后剩余点的集合;
(3.1)具体的计算表示:g(A,{B,C,D}) = min{w(A,B)+g(B,{C,D})},其中w(A,B)是已知的,那么问题就转发成了求g(B,{C,D}了;
g(B,{C,D} = min{g(B,C)+g(C,{D})} 或 = min{w(B,D)+g(D,{C})},问题又转换成了求g(C,{D})和g(D,{C})了,这两个等价于w(C,D)和w(D,C);
(3.2)上面分解了g(A,{B,C,D}) = min{w(A,B)+g(B,{C,D})},这只是其中一个分支,还需要用同样的方法求另外两个分支:g(A,{B,C,D}) = min{w(A,C)+g(C,{B,D})} 和g(A,{B,C,D}) = min{w(A,D)+g(D,{C,D})}
所有分支求出来后,找到最小的分支就是最终的结果!
这两个算法非常经典,思路也很成熟了,github上的代码有一堆,感兴趣的小伙伴可以自行去找找尝试尝试!
注意:TSP解决的算法还有遗传算法、模拟退火等,上述算法叫深度优先遍历(俗称“使蛮力”),只是众多算法中的一种;
参考:
1、https://www.bilibili.com/video/BV1gz4y1S7jD?p=31 动态规划
2、https://www.油管.com/watch?v=hh-uFQ-MGfw Traveling Salesman Problem using Dynamic Programming | DAA (需要自备梯子;印度人讲的,动态演示整个过程,通俗易懂;除了口音听着憋屈,其他没毛病!)