Java常用算法二：分治法

文章目录

• 一、分治算法的基本步骤
• 二、分治算法解决汉诺塔问题
• 2.1 汉诺塔的规则：
• 2.2 使用分治算法

笔记参考：尚硅谷

分治法就是把很复杂的问题分而治之，把一个很大的问题分成几个很小的问题，再把这几个很小的问题分成很多个更小的问题。直到子问题可以简单地直接求解，那么原问题的解就是子问题解的集合。

分治算法可以解决：

• 二分搜索
• 大整数乘法
• 棋盘覆盖
• 合并排序
• 快速排序
• 线性时间选择
• 最接近点对问题
• 循环赛日程表
• 汉诺塔

---

一、分治算法的基本步骤

分治法在每一层递归上都有三个步骤:

1. 分解:将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
2. 解决: 若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3. 合并: 将各个子问题的解合并为原问题的解。

二、分治算法解决汉诺塔问题

2.1 汉诺塔的规则：

有三根杆子A，B，C。
A杆上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。
要求按下列规则将所有圆盘移至 C 杆：
每次只能移动一个圆盘；
大盘不能叠在小盘上面。
提示：可将圆盘临时置于 B 杆，也可将从 A 杆移出的圆盘重新移回 A 杆，但都必须遵循上述两条规则。
问：如何移？最少要移动多少次？

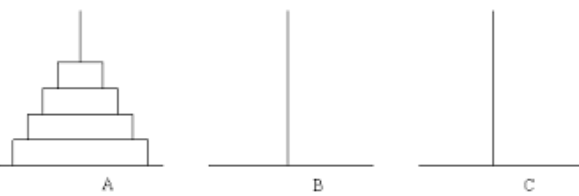
1. 如果是有一个盘， A->C
   如果我们有 N>=2 情况，我们总是可以看做是两个盘1.最下边的盘 2.上面的盘
2. 先把最上面的盘A->B
3. 把最下边的盘A->C
4. 把B塔的所有盘从B->C

2.2 使用分治算法

public class Hanoitower {
	public static void main(String[] args) {
		hanoiTower(5, 'a', 'b', 'c');
	}
	
	// a 是 source
	// b 是 middle
	// c 是 target
	public static void hanoiTower( int num, char a, char b, char c) {
		if(num == 1)
			//问题较小，直接解决
			System.out.println("第1个盘从" + a + "->" + c);
		else {
			//如果我们有 n>=2 情况，我们总是可以看做是两个盘 1.最下边的一个盘 2.上面的所有盘
			// 1. 先把最上面的所有盘A->B， 移动过程会使用c作为中间站
			hanoiTower(num-1, a, c, b);
			// 2. 再把最后一个盘从a->C
			System.out.println("第" + num+ "个盘从" + a + "->" + c); 
			// 3. 把上面的所有盘从b->c，移动过程会使用a作为中间站
			hanoiTower(num-1, b, a, c);
		}
	}
}