匹配追踪的过程已经在匹配追踪算法(MP)简介中进行了简单介绍,下面是使用Python进行图像重建的实践。
MP算法Python版
MP算法原理:
算法假定输入信号与字典库中的原子在结构上具有一定的相关性,这种相关性通过信号与原子库中原子的内积表示,即内积越大,表示信号与字典库中的这个原子的相关性越大,因此可以使用这个原子来近似表示这个信号。当然这种表示会有误差,将表示误差称为信号残差,用原信号减去这个原子,得到残差,再通过计算相关性的方式从字典库中选出一个原子表示这个残差。迭代进行上述步骤,随着迭代次数的增加,信号残差将越来越小,当满足停止条件时终止迭代,得到一组原子,及残差,将这组原子进行线性组合就能重构输入信号。
MP算法的执行步骤如下:
输入:字典矩阵(mathrm{A}),信号向量(y),稀疏度(k).
输出:(x)的(k)稀疏逼近(hat{x}).
初始化:生成字典矩阵(mathrm{A})(这里使用离散余弦变换基DCT),残差(r_0 = y),索引集(Lambda_0 = emptyset),(t=1).
循环执行步骤1-5:
- 找出残差(r)和字典矩阵的列(mathrm{A}_i)积中最大值所对应的值(p)及脚标(lambda),即(p_t =max_{i=1,cdots, N}left|<r_{t-1},mathrm{A}_i> ight|).
- 更新索引集(Lambda_t = Lambda_{t-1} cup {lambda_t}),记录找到的字典矩阵中的重建原子集合(A_t = [A_{t-1}, A_{lambda_t}]).
- 更新稀疏向量(hat{x}_t = hat{x}_t cup {p_t}).
- 更新残差(r_t = y - A_t hat{x}_t),(t=t+1).
- 判断是否满足(t > k),若满足,则迭代停止;若不满足,则继续执行步骤1.
Python代码实现(针对二维图像):
import numpy as np
def bmp(mtx, codebook, threshold):
"""
:param mtx: 原始图像(mxn)
:param codebook: 字典(mxk)
:param threshold: 非零元素个数的最大值
:return: 稀疏编码系数
3 """
n = mtx.shape[1] if len(mtx.shape) > 1 else 1 # 原始图像mtx中向量的个数
k = codebook.shape[1] # 字典dictionary中向量的个数
result = np.zeros((k, n)) # 系数矩阵result中行数等于dictionary中向量的个数,列数等于mtx中向量的个数
for i in range(n):
indices = [] # 记录选中字典中原子的位置
coefficients = [] # 存储系数向量
residual = mtx[:, i]
for j in range(threshold):
projection = np.dot(codebook.T, residual)
# 获取内积向量中元素绝对值的最大值
max_value = projection.max()
if abs(projection.min()) >= abs(projection.max()):
max_value = projection.min()
pos = np.where(projection == max_value)[0]
indices.append(pos.tolist()[0]) # 只存储在字典中的列(因为计算过程中对codebook进行了转置,所以这里取第一个元素)
coefficients.append(max_value)
residual = mtx[:, i] - np.dot(codebook[:, indices[0: j + 1]], np.array(coefficients))
if (residual ** 2).sum() < 1e-6:
break
for t, s in zip(indices, coefficients):
result[t][i] = s
return result
基于MP的图像重建
对于较大的图像,进行分块处理,使用im2col和col2im函数进行图像的分块和分块后的重建(参考:Python中如何实现im2col和col2im函数)。
这样字典矩阵的行数就仅仅和分块矩阵的大小有关,和原始图像的大小没有关系了。我们可以使用规模较小的字典矩阵表征较大的图像。
Python代码实现:
import numpy as np
from scipy import fftpack
import math
import mahotas as mh
import matplotlib.pyplot as plt
import mp.mpalg
def dct2(mtx):
return fftpack.dct(fftpack.dct(mtx.T, norm='ortho').T, norm='ortho')
def idct2(mtx):
return fftpack.idct(fftpack.idct(mtx.T, norm='ortho').T, norm='ortho')
def dctmtx(n):
basis = np.zeros((n, n))
for i in range(n):
c = math.sqrt(2 / n) if i != 0 else math.sqrt(1 / n)
for j in range(n):
basis[i, j] = c * math.cos((j + 0.5) * math.pi * i / n)
return basis
def im2col(mtx, block_size):
mtx_shape = mtx.shape
sx = mtx_shape[0] - block_size[0] + 1
sy = mtx_shape[1] - block_size[1] + 1
# 如果设A为m×n的,对于[p q]的块划分,最后矩阵的行数为p×q,列数为(m−p+1)×(n−q+1)。
result = np.empty((block_size[0] * block_size[1], sx * sy))
# 沿着行移动,所以先保持列(i)不动,沿着行(j)走
for i in range(sy):
for j in range(sx):
result[:, i * sx + j] = mtx[j:j + block_size[0], i:i + block_size[1]].ravel(order='F')
return result
def col2im(mtx, image_size, block_size):
p, q = block_size
sx = image_size[0] - p + 1
sy = image_size[1] - q + 1
result = np.zeros(image_size)
weight = np.zeros(image_size) # weight记录每个单元格的数字重复加了多少遍
col = 0
# 沿着行移动,所以先保持列(i)不动,沿着行(j)走
for i in range(sy):
for j in range(sx):
result[j:j + p, i:i + q] += mtx[:, col].reshape(block_size, order='F')
weight[j:j + p, i:i + q] += np.ones(block_size)
col += 1
return result / weight
def sparse_encode(image, block_size, codebook, threshold):
blocks = im2col(image, block_size)
return mp.mpalg.bmp(blocks, codebook, threshold)
def sparse_decode(coefficients, codebook, image_size, block_size):
blocks = np.dot(codebook, coefficients)
return col2im(blocks, image_size, block_size)
if __name__ == '__main__':
image = mh.imread('Lenna.jpg')
image = mh.colors.rgb2gray(image)
image_size = image.shape
block_size = (8, 8)
codebook = dctmtx(block_size[0] * block_size[1])
threshold = 30
coefficients = sparse_encode(image, block_size, codebook, threshold)
reconstructed = sparse_decode(coefficients, codebook, image_size, block_size)
plt.gray()
plt.subplot(121)
plt.title('原始图像')
plt.imshow(image)
plt.subplot(122)
plt.title('稀疏重建')
plt.imshow(reconstructed)
plt.show()
下面是分别设置threshold为10,20和30的运行结果:
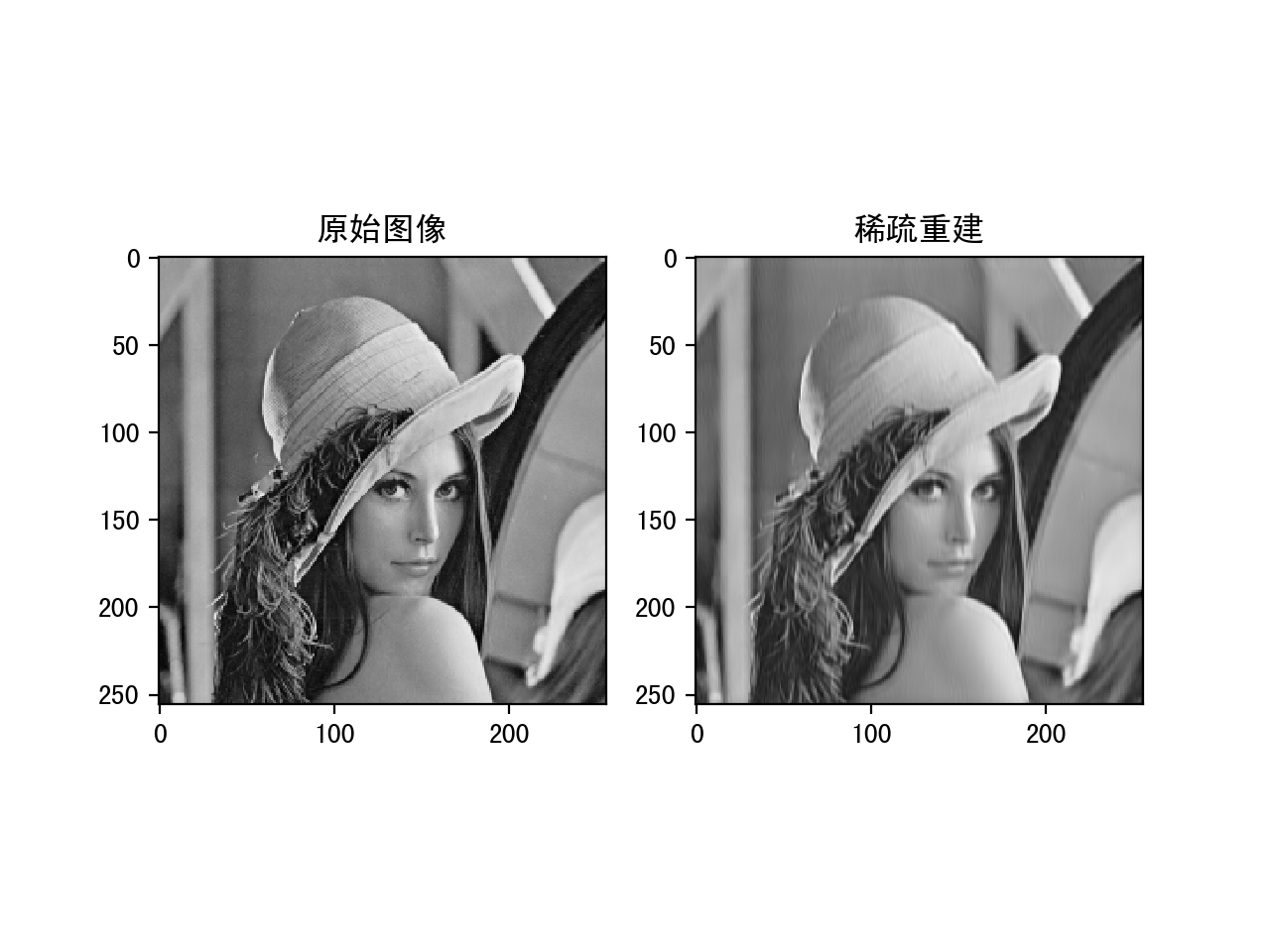
稀疏系数设置为10的重建结果
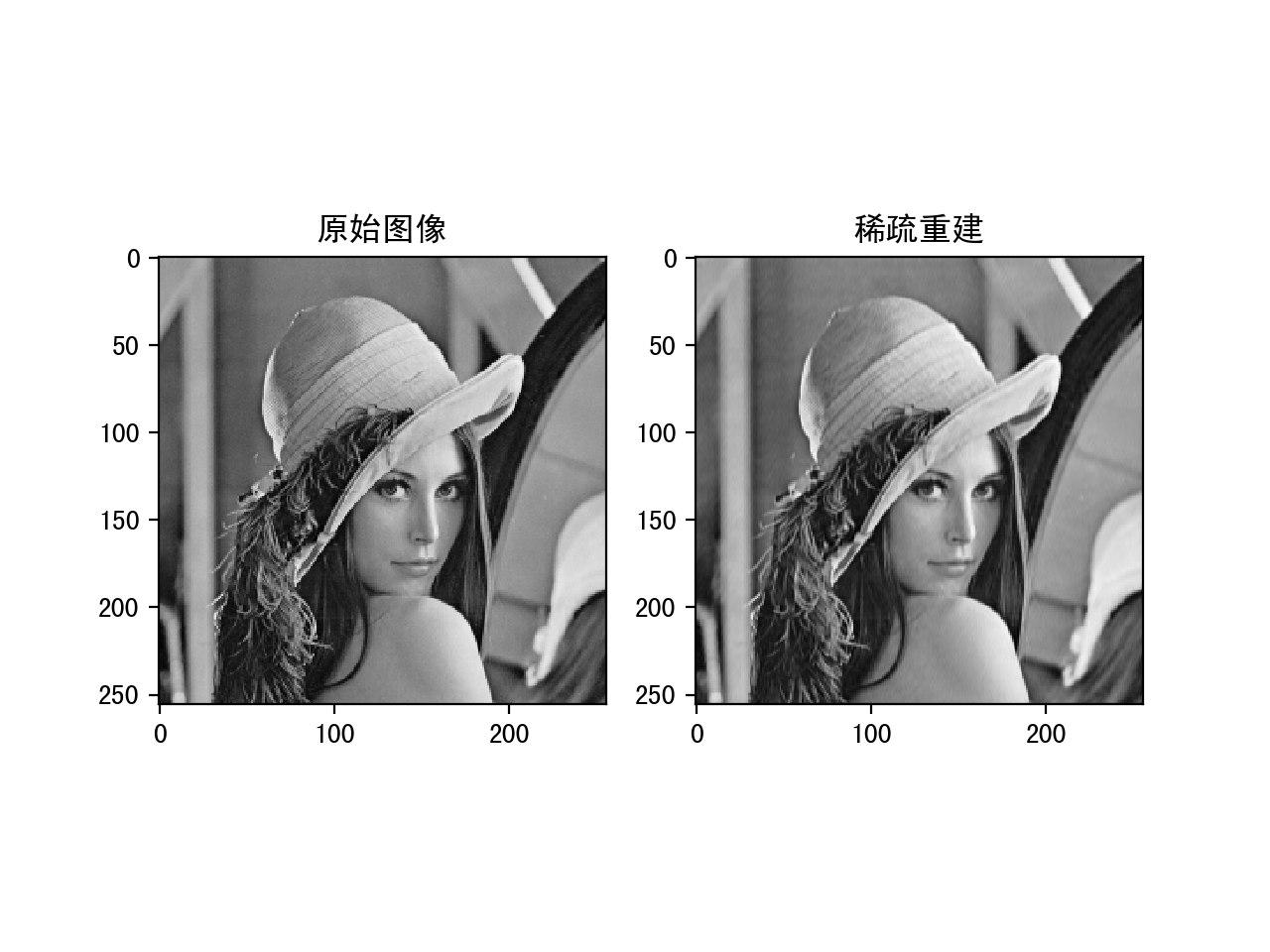
稀疏系数设置为20的重建结果
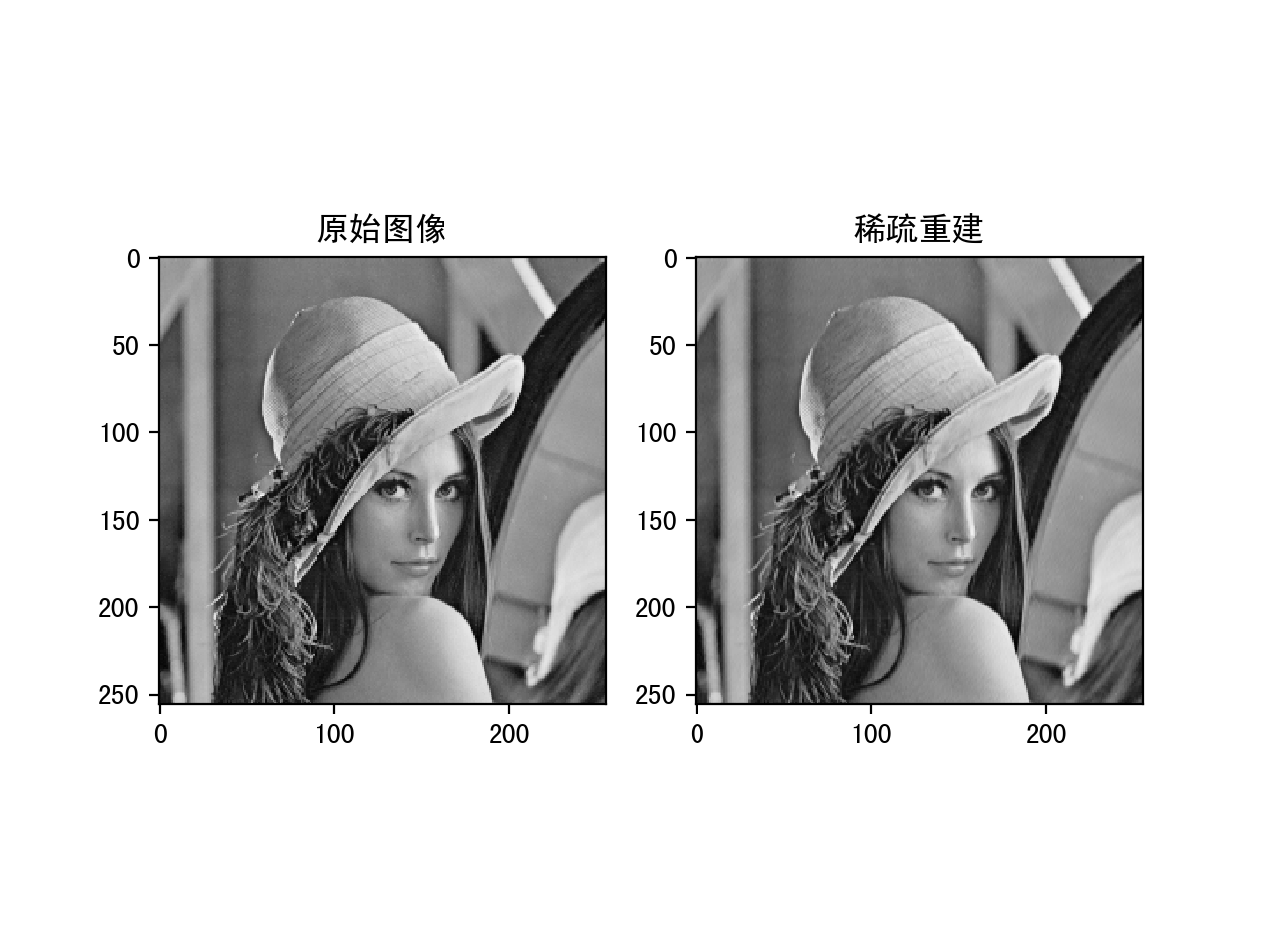
稀疏系数设置为30的重建结果
可以看到随着稀疏值的增大,重建的的结果会越来越好,但是稀疏度降低。这中间需要一个平衡。