转载：http://www.cnblogs.com/hxsyl/p/3290832.html
为什么写这个呢？因为那天听到了这个词，属于MST的扩展……最小K度树有空研究。
一.理论准备
需要读者事先懂得prime算法，不太了解的请看博主这一篇http://www.cnblogs.com/hxsyl/p/3286956.html，也需要读者对DP了解一些。
先看一个结论：次小生成树可由最小生成树换一条边得到，笔者认为很有必要搞清楚这一点，，否则对算法理解不够深入。
证明:咱换种方式去看待这个结论(一个生成树可以通过换边得到另一个生成树)，T是某一棵最小生成树，T0是任一棵异于T的生成树，通过变换T0 --> T1 --> T2 --> ... --> Tn (T) 变成最小生成树。所谓的变换是，每次把Ti中的某条边换成T中的一条边, 而且树T(i+1)的权小于等于Ti的权。
看下面的具体步骤(一定要理解透彻)。
step 1. 在Ti中任取一条不在T中的边uv.
step 2. 把边uv去掉，就剩下两个连通分量A和B，在T中，必有唯一的边u'v' 连结A和B。这是为什么呢？因为生成树中任意两点间只有一条路径(下面也要用这个)，且必有一条。
step 3. 显然u'v'的权比uv小 (prime算法贪心的，否则,uv就应该在T中)，把u'v'替换uv即得树T(i+1)。
特别地：取T0为任一棵次小生成树，T(n-1) 也就是次小生成树且跟T差一条边， 结论得证。
下面看具体算法。
step 1. 先用prim求出最小生成树T，在prim的同时，用一个矩阵maxd[u][v] 记录 在T中连结任意两点u,v的唯一的路中权值最大的那条边的权值.(有些拗口)，这是很容易做到的，因为prim是每次增加一个结点s, 在此需要保存节点和其父节点，采用DP，则最大权值要么是新加入的边，要么是父节点到起始点的采用DP算出来的距离，如下：
//u是刚加入的点，不过还没进入节点数组，v是已经存在的点
//min是按prime新加入那条边
maxd[v][u] = maxd[u][v] = max{min，maxd[father[u]][v]}
//u是刚加入的点，不过还没进入节点数组，v是已经存在的点//min是按prime新加入那条边maxd[v][u] = maxd[u][v] = max{min，maxd[father[u]][v]} 该步骤用时 O(V^2)，就是prime算法的耗时。 step 2. 枚举所有不在T中的边uv, 加入边uv则必然替换权为maxd[u][v]的边，这样才能保证次小。二.算法实现 以POJ1679为例，判断最小生成树是否唯一(不唯一可能是重边，不过一般在做题里不可能，否则没法建图，另外就是一般情况了，看下图)。
下面这三个图都是MST，权值161。234
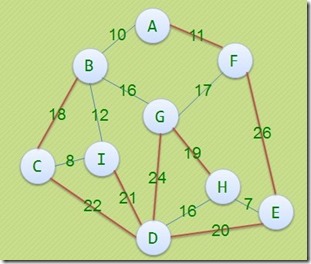
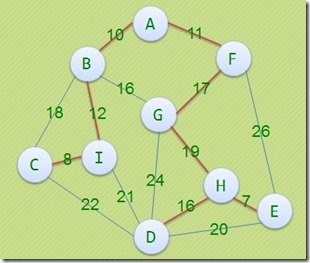
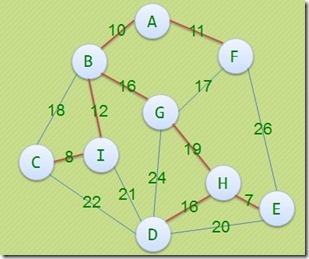
只要最小生成树和次小生成树权值和一样就唯一。因此得出如下算法，首先计算出最小生成树T，然后对最小生成树上任意不相邻的两个点 uv添加最小生成树以外的存在的边形成环，然后寻找u与v之间最小生成树上最长的边删去，计算map[i][j]与 maxd[i][j差值，求出最小的来，如果是0，就说明MST和次小生成树一样。
//顶点数100，看成了1000，一个MLE，改了立马AC，嘿嘿
//这道题目，AC率很低
import java.util.Scanner;
public class POJ1679 {
static int maxn = 105;
static int[][] map = new int[maxn][maxn];
static int[][] maxd = new int[maxn][maxn];
static int[] father = new int[maxn];
static int[] dist = new int[maxn];
static boolean[] vis = new boolean[maxn];
static int n,m;
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int num = sc.nextInt();
int u,v,w;
while(num-->0) {
n = sc.nextInt();
m = sc.nextInt();
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
if(i==j) {
map[i][j] = 0;
}else {
map[i][j] = 0x3f3f3f3f;
}
maxd[i][j] = -1;
}
}
for(int i=0; i<m; i++) {
u = sc.nextInt();
v = sc.nextInt();
w = sc.nextInt();
map[u][v] = w;
map[v][u] = w;
}
int ans = prime();
int min = 0x3f3f3f3f;
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
boolean tag = i!=j&&map[i][j]!=0x3f3f3f3f
&&father[i]!=j&&father[j]!=i;
if(tag) {
if(min>map[i][j]-maxd[i][j]) {
min = map[i][j]-maxd[i][j];
}
}
}
}
if(0==min) {
System.out.println("Not Unique!");
}else {
System.out.println(ans);
}
}
}
private static int prime() {
int ans = 0;
for(int i=1; i<=n; i++) {
dist[i] = map[1][i];
father[i] = 1;
vis[i] = false;
}
vis[1] = true;
//存放MST节点
int stack[] = new int[n+1];
int top = 0;
stack[top++] = 1;
for(int i=1; i<n; i++) {
int next = 1;
int min = 0x3f3f3f3f;
for(int j=1; j<=n; j++) {
if(!vis[j]&&min>dist[j]) {
next = j;
min = dist[j];
}
}
vis[next] = true;
ans += min;
//dp
for(int k=0; k<top; k++) {
maxd[next][stack[k]] = maxd[stack[k]][next]
= Math.max(min,maxd[father[next]][stack[k]]);
}
stack[top++] = next;
for(int t=1; t<=n; t++) {
if(!vis[t]&&dist[t]>map[next][t]) {
dist[t] = map[next][t];
father[t] = next;
}
}
}
return ans;
}
}
作者：张朋飞
出处：http://www.cnblogs.com
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.
只要最小生成树和次小生成树权值和一样就唯一。因此得出如下算法，首先计算出最小生成树T，然后对最小生成树上任意不相邻的两个点 uv添加最小生成树以外的存在的边形成环，然后寻找u与v之间最小生成树上最长的边删去，计算map[i][j]与 maxd[i][j差值，求出最小的来，如果是0，就说明MST和次小生成树一样。