简单说一下图像傅里叶变换的思路。
文章思路，先理解傅里叶级数，由连续傅里叶级数说明傅里叶变换。之后引入取样函数，对连续函数取样，就可以得到离散函数的傅里叶变换。由此推倒出单变量傅里叶变换。由一维傅里叶变换，就可以推导出二维傅里叶变换，及图像的傅里叶变换。下一篇博客再讲图像傅里叶变换性质。
https://www.zhihu.com/question/19714540
这篇文章很详细讲述了傅里叶变换公式
https://zhuanlan.zhihu.com/p/19759362
这篇文章没有公式，很清晰讲述了傅里叶变换的意义。就不再多说，这里只是简单列一下我理解的思路。
对于连续变量t,傅里叶级数为
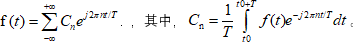其实Cn就是频域基的系数，频域就是以
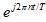为基的坐标系。
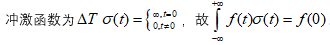
由傅里叶级数可知，连续变量的傅里叶变换如下：
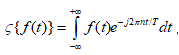，其实就是求的频率域的系数，反变换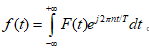 
若对冲击函数对做傅里叶变换，其频率域的冲激函数也是冲激函数对。
可由取样函数将连续函数傅里叶变换推广到离散傅里叶变换。使用冲激函数对连续傅里叶函数取样，就得到了离散傅里叶函数。对离散函数做傅里叶变换。
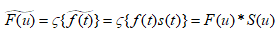
对两个函数的积做傅里叶变换，相当于对两个函数的傅里叶变换做卷积。
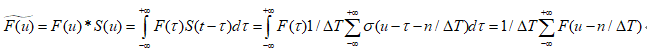
其实相当于将连续函数的傅里叶变换做无限平移，平移距离为1/T。此处插入取样定理， 1/T必须大于umax-umin,即频域率的一个周期。
如图：
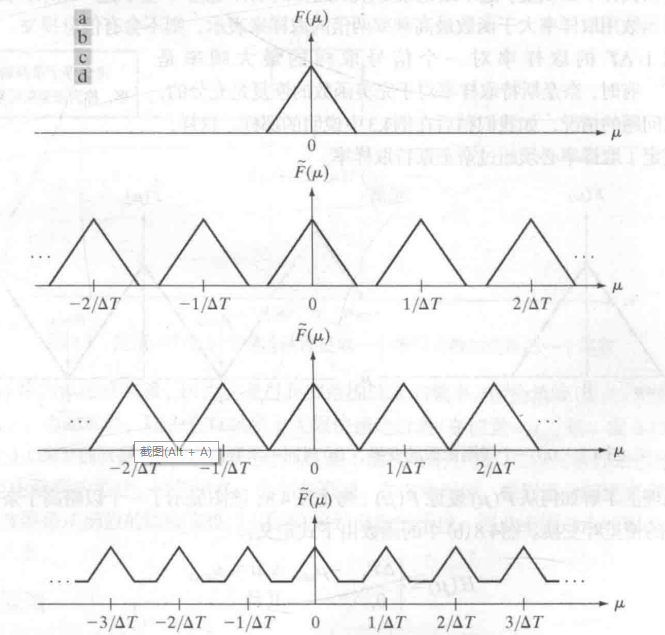
由对连续函数取样，做傅里叶变换，可推广到单变量的傅里叶变换。
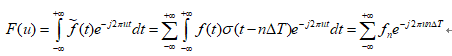
其中，取样频率，若要在T内取M个样本，则取样频率为u=m/M,m=0,1,2,3,4
图像就是将一维傅里叶变换扩展到二维。
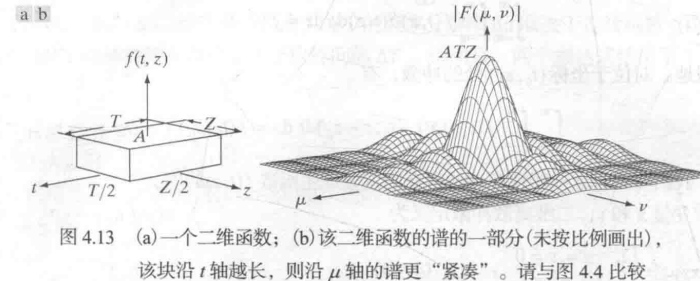
图像傅里叶变换特点
平移和旋转
若对图像进行傅里叶变换，在频域进行平移，需要在空间域乘一个系数，公式如下。单纯平移不影响傅里叶谱。
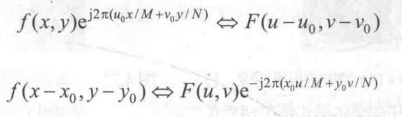
旋转：
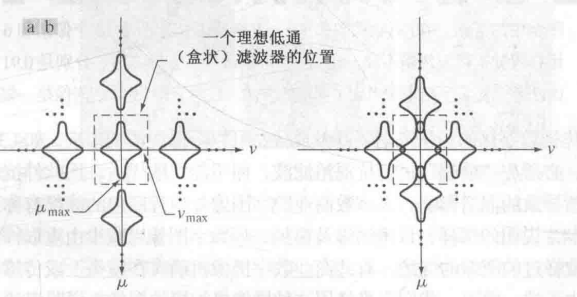
周期性
二维傅里叶变换及其反变换在u方向和v方向都是无限周期的，即
由前面离散傅里叶变化可以得到该性质
由周期性和平移特性可知，我们若想让图像在频域呈现一个完整的周期，需要对图像做一个平移。通常做法是在空间域乘-1
对称性
实函数的傅里叶变换频谱是共轭对称的，即F(u,v)=F(-u,-v)
若要避免混淆，一般需要对图像做双倍的填充，之后再对图像进行裁剪。整个的图像傅里叶变换流程如下:
最后，对某些图像做一些傅里叶变换，并附上代码：
Mat get_freq(Mat src)
{
Mat srcGray;
cvtColor(src, srcGray, CV_RGB2GRAY); //灰度图像做傅里叶变换
int m = getOptimalDFTSize(srcGray.rows); //2,3,5的倍数有更高效率的傅里叶变换
int n = getOptimalDFTSize(srcGray.cols);
Mat padded;
//把灰度图像放在左上角,在右边和下边扩展图像,扩展部分填充为0;
copyMakeBorder(srcGray, padded, 0, m - srcGray.rows, 0, n - srcGray.cols, BORDER_CONSTANT, Scalar::all(0));
//cout << padded.size() << endl;
//这里是获取了两个Mat,一个用于存放dft变换的实部，一个用于存放虚部,初始的时候,实部就是图像本身,虚部全为零
Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };
Mat complexImg;
//将几个单通道的mat融合成一个多通道的mat,这里融合的complexImg既有实部又有虚部
merge(planes, 2, complexImg);
//对上边合成的mat进行傅里叶变换,支持原地操作,傅里叶变换结果为复数.通道1存的是实部,通道二存的是虚部
dft(complexImg, complexImg);
//把变换后的结果分割到两个mat,一个实部,一个虚部,方便后续操作
split(complexImg, planes);
//这一部分是为了计算dft变换后的幅值，傅立叶变换的幅度值范围大到不适合在屏幕上显示。高值在屏幕上显示为白点，而低值为黑点，高低值的变化无法有效分辨。
//为了在屏幕上凸显出高低变化的连续性，我们可以用对数尺度来替换线性尺度,以便于显示幅值,计算公式如下:
//=> log(1 + sqrt(Re(DFT(I))^2 +Im(DFT(I))^2))
magnitude(planes[0], planes[1], planes[0]);
Mat mag = planes[0];
mag += Scalar::all(1);
log(mag, mag);
//crop the spectrum, if it has an odd number of rows or columns
//修剪频谱,如果图像的行或者列是奇数的话,那其频谱是不对称的,因此要修剪
//这里为什么要用 &-2这个操作，我会在代码后面的 注2 说明
mag = mag(Rect(0, 0, mag.cols & -2, mag.rows & -2));
Mat _magI = mag.clone();
//这一步的目的仍然是为了显示,但是幅度值仍然超过可显示范围[0,1],我们使用 normalize() 函数将幅度归一化到可显示范围。
normalize(_magI, _magI, 0, 1, CV_MINMAX);
//imshow("before rearrange", _magI);
//rearrange the quadrants of Fourier image
//so that the origin is at the image center
//重新分配象限，使（0,0）移动到图像中心，
//在《数字图像处理》中，傅里叶变换之前要对源图像乘以（-1）^(x+y)进行中心化。
//这是是对傅里叶变换结果进行中心化
int cx = mag.cols / 2;
int cy = mag.rows / 2;
Mat tmp;
Mat q0(mag, Rect(0, 0, cx, cy)); //Top-Left - Create a ROI per quadrant
Mat q1(mag, Rect(cx, 0, cx, cy)); //Top-Right
Mat q2(mag, Rect(0, cy, cx, cy)); //Bottom-Left
Mat q3(mag, Rect(cx, cy, cx, cy)); //Bottom-Right
//swap quadrants(Top-Left with Bottom-Right)
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
// swap quadrant (Top-Rightwith Bottom-Left)
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);
normalize(mag, mag, 0, 1, CV_MINMAX);
return mag;
}
图像变换结果：
条纹状，观察其对称性：
可以看到中心的斜线与原图像条纹垂直。这和条纹的明暗变化方向一致。