imetime series data mining主要包括decompose(分析数据的各个成分,例如趋势,周期性),prediction(预测未来的值),classification(对有序数据序列的feature提取与分类),clustering(相似数列聚类)等。时序数据prediction(forecast,预测)使用最广泛的两个算法: Holt-Winters 和 ARIMA。其它的常用函数说明如下:
- stats::ts() --生成时序对象
- stats::start() --返回时间序列的开始时间
- stats::end() --返回时间序列的开始时间
- stats::frequency --返回时间序列中时间点的个数
- stats::window() --对时间序列取子集
- graphics::plot() --画出时间序列拆线图
- stats::monthplot() --画出时序中的季节项
- forecast::seasonplot --生成季节图
- stats::stl() -- 用 LOESS光滑将时序分解为季节项、趋势项和随机项。局限之处——只能处理相加模型
- stats::decompose() -- 对相加与相乘模型都可以直接进行季节分解
- forecast::ma() -- 拟合一个简单的移动平均模型
- stats::HoltWinters() -- 三次平滑指数法,拟合指数平常模型
- forecast::ets() -- 拟合指数平滑模型,同时也可以自动选取最优模型
- forecast::accuracy() -- 返回时序的拟合优度度量
- tseries::adf.test() -- 对序列做ADF检验以判断其是否平稳
- stats::lag() -- 返回取过指定滞后项后的时序
- base::diff() -- 返回取过滞后项和差分后的序列
- forecast::ndiffs() -- 找到最优差分次数以移除序列中的趋势项
- forecast::acf() -- 估计自相关函数
- forecast::pacf() -- 估计偏自相关函数
- stats::arima() -- 似合 ARIMA模型
- forecast::auto.arima() --自动选择 ARIMA模型,可能不准确
- forecast::forecast() --预测时序的未来值
- stats::Box.test() -- 进行Ljung-Box 检验以判断模型的残差是否独立
- tseries::bds.test() -- 进行BDS检验以判断序列中的随机变量是否服从独立分布
stats::ts(): 生成时序对象
ts(data, frequency=n, start=x, end=y, names=c(a,b,c,...))
- data: 观察到的时间序列值的向量或矩阵。
- frequency: 频次,n=1 为年, n=4为季度,n=7 为周, n=12 为月等
- start: 起始时点
-
> t <- ts(testSrc$tp,start = c(2016,1),frequency= 12) > start(t) [1] 2016 1 > end(t) [1] 2017 12 > frequency(t) [1] 12 - 按天时间段
-
> library(zoo) > zoo <- zoo(testSrc$dp,order.by = as.Date(as.character(testSrc$biztime), format='%Y-%m-%d')) > ts <- ts(zoo) > str(ts) Time-Series [1:742] from 1 to 742: 62772 57541 59310 66895 71020 ... - attr(*, "index")= Date[1:742], format: "2016-01-01" "2016-01-02" "2016-01-03" "2016-01-04" ... - 另一种写法:
-
xl<- ts(testSrc$dp,start=c(2016,01,01),frequency=365) str(xl)
stats::decompose() 对相加与相乘模型都可以直接进行季节分解
decompose(x, type = c("additive", "multiplicative"), filter = NULL)
-
xl<- ts(testSrc$dp,start=c(2016,01,01),frequency=365) ##季节分解 ml <- decompose(xl,c("multiplicative")) plot(ml) 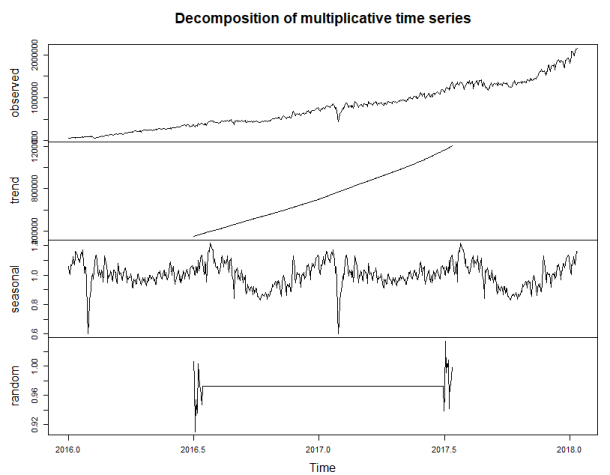
- 在分解季节成分的基础上,如果有需要的话,我们可以对时间序列进行季节因素调整,将这一部分信息从原始数据中去除。
-
xl<- ts(testSrc$dp,start=c(2016,01,01),frequency=365) ##季节分解 ml <- decompose(xl,c("multiplicative")) plot(ml) data2 <- xl - ml$seasonal par(mfrow=c(1,2)) plot(xl) plot(data2) 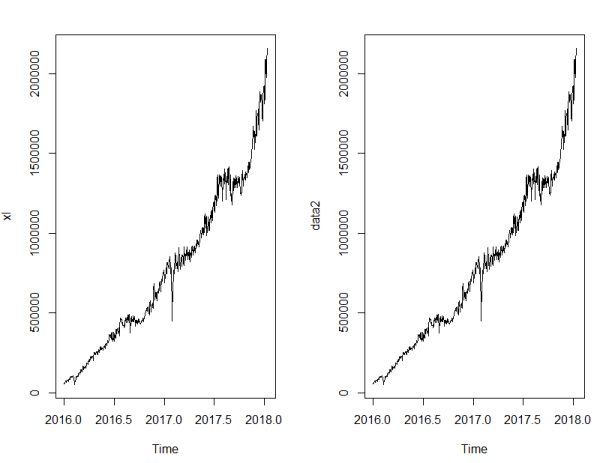
forecast::ets():拟合指数平滑模型
ets(ts, model="ZZZ",.....)
- 限制模型的字母有三个。第一个字母代表误差项,第二个字母代表趋势项,第三个字母则代表季节项。
- 可选的字母包括:相加模型(A)、相乘模型(M)、无(N)、自动选择(Z)。
通过ets()函数自动选取对原始数据拟合优度最高的模型。
-
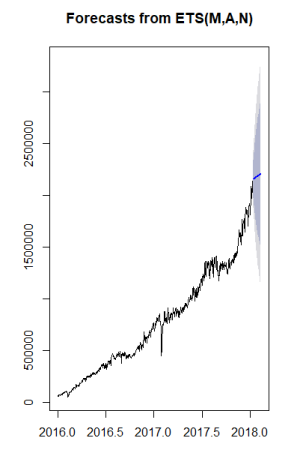
> library(forecast) > x <- ets(data2) Warning message: In ets(data2) : I can't handle data with frequency greater than 24. Seasonality will be ignored. Try stlf() if you need seasonal forecasts. > x ETS(M,A,N) Call: ets(y = data2) Smoothing parameters: alpha = 0.9999 beta = 1e-04 Initial states: l = 60125.3605 b = 1757.7865 sigma: 0.0459 AIC AICc BIC 20049.03 20049.12 20072.08 > plot(x) - 效果图

- 预测
-
> pre <- forecast(x,h=30) > pre$mean Time Series: Start = c(2018, 13) End = c(2018, 42) Frequency = 365 [1] 2159078 2160914 2162751 2164588 2166424 2168261 2170097 2171934 2173771 2175607 2177444 2179281 2181117 2182954 2184790 [16] 2186627 2188464 2190300 2192137 2193974 2195810 2197647 2199483 2201320 2203157 2204993 2206830 2208667 2210503 2212340 > plot(pre)