基于划分方法聚类算法R包:
- K-均值聚类(K-means) stats::kmeans()、fpc::kmeansruns()
- K-中心点聚类(K-Medoids) cluster::pam() 、fpc::pamk()
- 层次聚类 stats::hclust()、BIRCH、CURE
- 密度聚类 fpc::DBSCAN(),OPTICS
- 网格聚类 optpart::clique
- 模型聚类 EM算法(期望最大化算法) mclust::Mclust() 、RWeka::Cobweb()
- 模糊聚类 FCM(Fuzzy C-Means)算法 cluster::fanny() 、e1071::cmeans()
K均值聚类
- stats::kmeans()
- fpc::kmeansruns()
stats::kmeans()
Usage:kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"), trace=FALSE)
- x:聚类对象
- centers: 是聚类个数或者是聚类中心
- iter.max:是允许的最大迭代次数,默认为10
- nstart:是初始被随机选择的聚类中心
示例代码
##数据集进行备份
newiris <- iris
newiris$Species <- NULL
library(stats)
kc <- kmeans(x=newiris, centers = 3)
##查看具体分类情况
fitted(kc)
##在三个聚类中分别统计各种花出现的次数
table(iris$Species, kc$cluster)
查看运行结果,产生了3个聚类,如下解释:
> kc
K-means clustering with 3 clusters of sizes 62, 50, 38 #K-means算法产生了3个聚类,大小分别为38,50,62.
Cluster means: #每个聚类中各个列值生成的最终平均值
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.901613 2.748387 4.393548 1.433871
2 5.006000 3.428000 1.462000 0.246000
3 6.850000 3.073684 5.742105 2.071053
Clustering vector: #每行记录所属的聚类(2代表属于第二个聚类,1代表属于第一个聚类,3代表属于第三个聚类) [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[71] 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 3 3 3 3 1 3 3 3 3 3 3 1 1 3 3 3 3 1 3 1 3 1 3 3 1 1 3 3 3 3 3 1 3 3 3 3 1 3
[141] 3 3 1 3 3 3 1 3 3 1
Within cluster sum of squares by cluster: #每个聚类内部的距离平方和,说明第一类样本点差异最大,第二类差异最小
[1] 39.82097 15.15100 23.87947
(between_SS / total_SS = 88.4 %)
#组间的距离平方和占了整体距离平方和的的88.4%,这个值越大表明组内差距越小,组间差距越大,即聚类效果越好该值可用于与类别数取不同值时的聚类结果进行比较。
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" "iter" "ifault"
#"cluster"是一个整数向量,用于表示记录所属的聚类
#"centers"是一个矩阵,表示每聚类中各个变量的中心点
#"totss"表示所生成聚类的总体距离平方和
#"withinss"表示各个聚类组内的距离平方和
#"tot.withinss"表示聚类组内的距离平方和总量
#"betweenss"表示聚类组间的聚类平方和总量
#"size"表示每个聚类组中成员的数量
创建一个连续表,在三个聚类中分别统计各种花出现的次数
> ##在三个聚类中分别统计各种花出现的次数
> table(iris$Species, kc$cluster)
1 2 3
setosa 0 50 0
versicolor 48 0 2
virginica 14 0 36
根据最后的聚类结果画出散点图,数据为结果集中的列"Sepal.Length"和"Sepal.Width",颜色为用1,2,3表示的缺省颜色
> plot(newiris[c("Sepal.Length", "Sepal.Width")], col = kc$cluster)
在图上标出每个聚类的中心点
> points(kc$centers[,c("Sepal.Length", "Sepal.Width")], col = 1:3, pch = 8, cex=2)
生成图例 如下:
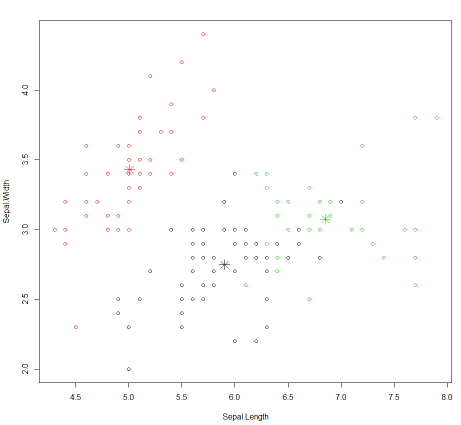
小结:
在这个示例中, 首先将数据集中变量品种全部置为空, 然后重新指定3个聚类,比较一下kmeans算法生成的结果和原有的结果。
在kmean算法中针对变量 Sepal.Length Sepal.Width Petal.Length Petal.Width生成三组随机值作为中心点,然后计算每个样本中的4个变量到随机值的距离,根据最新的随机数值总合算出平均值重新计算中心点。然后不断的重复此步骤, 直到中心点的值不再变化。最后再将样本值和最终生成的中心值作比较,距离最近的归属于这个中心值所代表的聚类。最后使用plot函数画图的时候, 可以发现kmeans算法最后生成的分类并不是特别理想,各个聚类之间的距离并不是很大。需要多运行几次。
fpc::kmeansruns()
fpc包kmeansruns函数,相比于kmeans函数更加稳定,而且还可以估计聚为几类
Usage: kmeansruns(data,krange=2:10,criterion="ch",iter.max=100,runs=100,scaledata=FALSE,alpha=0.001, critout=FALSE,plot=FALSE,...);
- krange: 聚类个数范围
- critout: logical. If TRUE, the criterion value is printed out for every number of clusters
- iter.max:是允许的最大迭代次数,默认为100
需要安装包
install.packages("lme4")
install.packages("fpc")
示例代码
> newiris <- iris
> newiris$Species <- NULL
> library(fpc)
>
> kc1 <- kmeansruns(data = newiris,krange = 1:5,critout = TRUE)
2 clusters 513.9245
3 clusters 561.6278
4 clusters 530.7658
5 clusters 495.5415
> ##kc1
> ##fitted(kc1)
> table(iris$Species, kc1$cluster)
1 2 3
setosa 0 0 50
versicolor 2 48 0
virginica 36 14 0
>
待验证:
fpc::cluster.stats()
小结:
指定聚类个数范围为:1:5, 但估计聚类结果为3,与kmeans方法相比,不需初始确定聚类个数
参考资料: