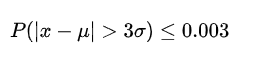离散度
标准差是反应一组数据离散程度最常用的一种量化形式,是表示精确度的重要指标。说起标准差首先得搞清楚它出现的目的。我们使用方法去检测它,但检测方法总是有误差的,所以检测值并不是其真实值。检测值与真实值之间的差距就是评价检测方法最有决定性的指标。但是真实值是多少,不得而知。因此怎样量化检测方法的准确性就成了难题。这也是临床工作质控的目的:保证每批实验结果的准确可靠。
虽然样本的真实值是不可能知道的,但是每个样本总是会有一个真实值的,不管它究竟是多少。可以想象,一个好的检测方法,其检测值应该很紧密的分散在真实值周围。如果不紧密,与真实值的距离就会大,准确性当然也就不好了,不可能想象离散度大的方法,会测出准确的结果。因此,离散度是评价方法的好坏的最重要也是最基本的指标。
一组数据怎样去评价和量化它的离散度呢?人们使用了很多种方法:
极差 :
- 最直接也是最简单的方法,即最大值-最小值(也就是极差)来评价一组数据的离散度。这一方法在日常生活中最为常见,比如比赛中去掉最高最低分就是极差的具体应用。
离均差的平方和
- 由于误差的不可控性,因此只由两个数据来评判一组数据是不科学的。所以人们在要求更高的领域不使用极差来评判。其实,离散度就是数据偏离平均值的程度。因此将数据与均值之差(我们叫它离均差)加起来就能反映出一个准确的离散程度。和越大离散度也就越大。但是由于偶然误差是成正态分布的,离均差有正有负,对于大样本离均差的代数和为零的。为了避免正负问题,在数学有上有两种方法:平均绝对偏差, 离均差平方求期望(即方差,即均差平方求期望,即均差平方和除以数量)是一个层面上的意思
- 一种是取绝对值,也就是常说的离均差绝对值之和。
- 而为了避免符号问题,数学上最常用的是另一种方法--平方,这样就都成了非负数。因此,离均差的平方和成了评价离散度一个指标。
方差(S2)
- 由于离均差的平方和与样本个数有关,只能反应相同样本的离散度,而实际工作中做比较很难做到相同的样本,因此为了消除样本个数的影响,增加可比性,将标准差(这里应该改为:离均差的平方)求平均值,这就是我们所说的方差成了评价离散度的较好指标。样本量越大越能反映真实的情况,而算数均值却完全忽略了这个问题,对此统计学上早有考虑,在统计学中样本的均差多是除以自由度(n-1),它的意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自由了,所以自由度是n-1。
标准差(SD)
- 由于方差是数据的平方,与检测值本身相差太大,人们难以直观的衡量,所以常用方差开根号换算回来这就是我们要说的标准差。 在统计学中样本的均差多是除以自由度(n-1),它是意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自由了,所以自由度是n-1。
变异系数(CV)
- 标准差能很客观准确的反映一组数据的离散程度,但是对于不同的检目,或同一项目不同的样本,标准差就缺乏可比性了,因此对于方法学评价来说又引入了变异系数CV。一组数据的平均值及标准差常常同时做为参考的依据。在直觉上,如果数值的中心以平均值来考虑,则标准差为统计分布之一“自然”的测量。
标准差与平均值定义公式
- 方差 s^2 = [(x1-x)^2+(x2-x)^2+......(xn-x)^2]/(n) (x为平均数)
- 标准差 = 方差的算术平方根
- 在实验中单次测量总是难免会产生误差,为此我们经常测量多次,然后用测量值的平均值表示测量的量,并用误差条来表征数据的分布,其中误差条的高度为±标准误。
正态分布
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为 μ、方差为 σ^2 的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布
正态分布具有两个参数 μ 和 σ^2 的连续型随机变量的分布:
- 第一个参数 μ: 是服从正态分布的随机变量的均值。
- 第二个参数σ^2:是此随机变量的方差,所以正态分布记作N(μ,σ2)
其中:
- μ 是正态分布的位置参数,描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大,而取离μ越远的值的概率越小。正态分布以X=μ为对称轴,左右完全对称。正态分布的期望、均数、中位数、众数相同,均等于μ
- σ 描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。也称为是正态分布的形状参数,σ越大,曲线越扁平,反之,σ越小,曲线越瘦高。
普通正态分布转换标准正态分布公式
- 正态分布是由两个参数 μ 与 σ 确定的。对于任意一个服从 N ( μ , σ 2 ) 分布的随机变量 X,经过下面的变换以后都可以转化为 μ = 0 , σ = 1 的标准正态分布(standard normal distribution)。转换公式为:
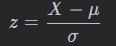
示例:
某专业招收研究生20名,其中有10名免费,报考人数为1000人,考试满分为500分。经过考试后才知道此专业考试总平均成绩为μ=300分,如果招收研究生的分数线确定为350分,试问,现在某人考360分,他有没有可能被录取为免费生?
- 研究生考试成绩X~N(μ,σ²),由已知 μ=300,而 σ 未知。研究生考试分数超过 350分 的考生频率应该近似等于事件 (X≥350) 的概率
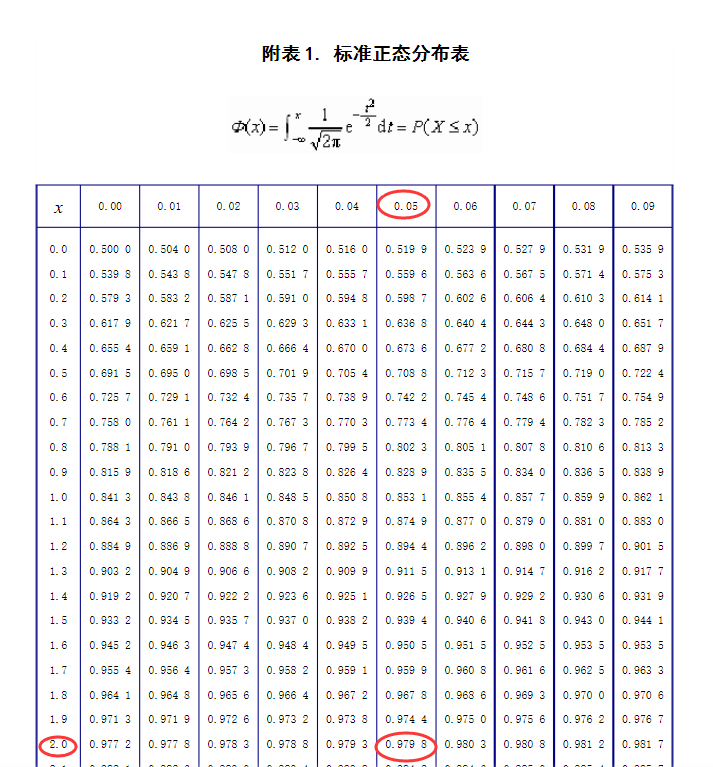
- 所以有 P(X≥350) = 20/1000=0.02,即 P(X<350) = 0.98,即 Φ((350-300)/σ)= 0.98
- 查标准正态分布表 Φ(2.05) = 0.9798 ≈ 0.98,如下图
- 所以取 50/σ = 2.05,解得 σ = 50/2.05
- 此人能否被录取为免费生,需估计一下他的排名,也就是算一下分数高于360分的概率,再乘以总人数就可以知道他的排名情况
- 因为 P(X≥360) = 1 - P(X<360) = 1 - Φ(60/σ) = 1 - Φ(60×2.05/50) = 1-Φ(2.46) = 1 - 0.9931 = 0.0069
- 所以研究生考试分数不低于360分的考生大概有:1000 × 0.0069 = 6.9 ≈ 7(人)
- 因此,在研究生考试中,该考得360分的考生大约排第7名,所以他有可能是免费生。
3sigma模型
检测异常,一般情况下超过一个阈值(threshold),那我们就可以粗略的认为这是一个异常数据,那阈值怎么定义:
- 第一:通过经验值,比如设置 threshold > 1000
- 第二:假设每次事件都是独立的且没有上下文关联,我们可以采用3sigma模型来检测
算法
数据需要服从正态分布。在3∂原则下,异常值如超过3倍标准差,那么可以将其视为异常值。正负3∂的概率是99.7%,那么距离平均值3∂之外的值出现的概率为P(|x-u| 3∂) = 0.003,属于极个别的小概率事件。如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
检测这一段时间的统计数据,假如符合正态分布,计算均值与方差。如果后来的统计值不在这个范围3sigma范围内,就可以认为这个值是异常值。
置信度和置信区间
- 3σ原则又称为拉依达准则,该准则具体来说,就是先假设一组检测数据只含有随机误差,对原始数据进行计算处理得到标准差,然后按一定的概率确定一个区间,认为误差超过这个区间的就属于异常值。
- 正态分布状况下,数值分布表:
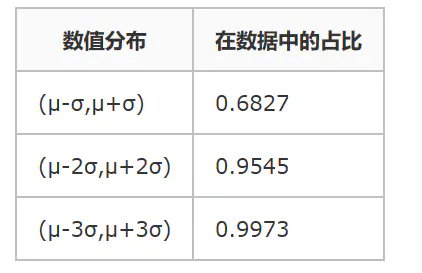
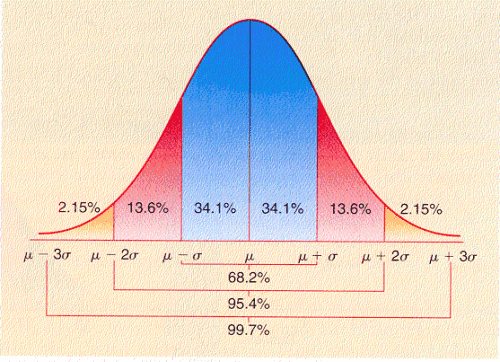
示例说明
做企业污染源检测,为了检测传感器是否正常,或者企业排放污染异常,你需要对传感器值做异常值的检测,假设企业每天排放污染是独立的,那么就可以使用简单粗暴的3sigma模型来检测。
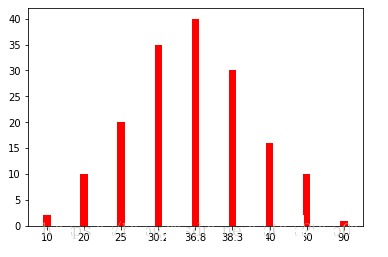
要知道企业的污染物排放是跟一个企业生产有关系的,如果一个企业正常生产那么污染物的排放量是不会相差太多。也就是说企业污染物排放量,会在一个范围内波动。对一个月的排放量,做一个简单的柱状图统计,x轴为排放量,y轴为排放次数。
通过图可以观察出,本月的排放还是挺符合正态分布的。如果取一个月的排放量为样本,那么就是样本容量为30,如果扩大采样数,进行统计的话。很明显可以看出,36.8为均值。如下图
采样估计
现在让你去评估该企业一天正常排放量是多少?假设企业真实污染物正常一天排放量为36.8。然后我们随机抽取一天,结果为30.2,你就说该企业正常排放量为30.2,这样显然不能让人认同。但是如果做了多天的样本抽样得出,[20,50]这个区间为污染物正常一天排放量的范围,显然这样更容易让人接受。但是能够让人多大程度接受呢?假设为95%,那么这里就引入置信区间[30.2,38.3]与置信度95%的概念。显然把所有天的排放量都采集回来做正常排放量估计是不合适的,因为每天都有新的数据加入,所以只能够以样本估计整体。
置信区间置信度案例解释
置信区间相信你有个大概想法,就是为认为这个排放量是正常的区间呗,那就是真实企业污染物正常排放量36.8,落在这个区间的概率吗?答案是否定的。为了帮助你理解这个拗口的话,
- 错误的理解计算置信度的方式是,统计在区间[30.2,38.3]的排放量的总个数除36.8的排放天数,结果为95%。
- 实际上正确的求解置信度的方式是,假设样本容量1000天,重新计算均值与方差,得到置信区间 。反复取这样的样本容量为1000 天 100次,那么就得到100个置信区间,这100个置信区间有95次包含了真实值36.8,95/100=95%,所以就得到置信度为95%。
但是这里又有个疑问,平时做置信区间的时候没有做100次啊,一般做一次,就得出了置信度为95%的置信区间。引入一个例子,把置信区间比喻为黑箱子里的球,有黑白两种颜色,抽样100次,统计得出95%为黑球,5%为白球。现在找另外一个人重黑箱子中抽一个球,问这个求是黑球的概率是多少?答案很显然 95%,所以我们经常只做一次抽样,得到置信区间就可以说,这个置信区间有95%的概率包含真实值。
那么异常值检测的思路就很清晰了,抽取一个月的数据,计算出置信区间,也就是说如果某天的排放量不在这个区间内,那么就可以说这天的值只有5%是一天正常的排放量,可能性很小那么就认为它是异常值。
代码示例
如前面所述,3sigma原理可以简单描述为:若数据服从正态分布,则异常值被定义为一组结果值中与平均值的偏差超过三倍标准差的值。即在正态分布的假设下,距离平均值三倍(为标准差)之外的值出现的概率很小(如下式),因此可认为是异常值。
若数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述(这就使该原理可以适用于不同的业务场景,只是需要根据经验来确定 k sigma中的k值,这个k值就可以认为是阈值)
示例代码参见: https://zhuanlan.zhihu.com/p/36297816
参考资料
- https://wenku.baidu.com/view/04e3515e6e85ec3a87c24028915f804d2a168777.html
- https://www.jianshu.com/p/9d05d11d6cb1?utm_campaign=maleskine&utm_content=note&utm_medium=seo_notes&utm_source=recommendation
- https://zhidao.baidu.com/question/652910531242338405.html
- https://blog.csdn.net/bitcarmanlee/article/details/86440851
- https://wenku.baidu.com/view/ea0ca1f24a35eefdc8d376eeaeaad1f3479311e5.html
- https://wenku.baidu.com/view/166967f39e3143323968931b.html
- https://blog.csdn.net/u014296502/article/details/80882296
- https://zhuanlan.zhihu.com/p/36297816