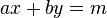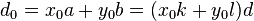【as+bt=1是ab两数互质的充要条件】
充分性,as+bt=1 => (a,b)=1:
因为as+bt=1,设c=(a,b),则c整除a和b,所以c整除as+bt,即c整除1,所以c=1,即a和b互质
必要性,(a,b)=1 => ab+bt=1:
考虑非空集合A={as+bt│s,t为任意整数},不妨设a0是A中最小正整数且a0=as0+bt0,y是A中任意一个元素,
由带余除法 y=as+bt=q(as0+bt0)+r,0<=r<a0,则r=a(s-qs0)+b(t-qt0)属于A,若r非零则r是A中比a0更小之正整数,矛盾,所以r=0,从而a0整除y。
因为a0整除y,所以 (as+bt)/a0 = q。=> as/a0+bt/a0 = q。s、t为任意值,而q必然为整数,则as/a0、bt/a0必须是整数。则有a0整除a,a0整除b,所以a0整除(a,b)=1,因此a0=1,所以存在整数s0和t0使得as0+bt0=1
【贝祖定理(裴蜀定理)】
有整数解时当且仅当m是d的倍数。d是(a,b)。裴蜀等式有解时必然有无穷多个整数解,每组解 、
、 都称为裴蜀数。在前部分证明的基础上,
都称为裴蜀数。在前部分证明的基础上,
对  和
和  的任意正公约数
的任意正公约数 ,设
,设 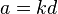 、
、 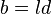 ,那么
,那么
因此 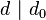 。所以
。所以  是
是  和
和  的最大公约数。
的最大公约数。
参考:http://zh.wikipedia.org/wiki/%E8%B2%9D%E7%A5%96%E7%AD%89%E5%BC%8F