【计算几何复习要点】
1、向量加法的几何含意:
a+b的释意为:a的尾连上b的头,新建一条从a的尾指向b的头的向量。
2、向量减法的几何含意:
a-b的释意为:尾部相连,新建一个从b的头指向a的头的向量。
3、点积,内积:
对于向量a(Xa,Ya)、向量b(Xb,Yb),a与b的点积为:Xa*Xb+Ya*Yb。
另外 a*b=|a|*|b|*cos(a与b夹角)。通过此公式可通过坐标来计算2向量夹角。
4、叉积。注意,axb 的结果是一个向量。
|aXb| = |a|*|b|*sin(a与b夹角)。几何函数为a向量与b向量组成的面积。
5、行数和列数相同的矩阵称为方阵。所有非对角线元素都为0的矩阵为对角矩阵。
6、转置矩阵意味着把矩阵给转换。
参考自《3D数学基础:图像与游戏开发》
【3D数学基础】
1、研究自然数、整数的领域称为离散数学。研究实数的领域称作连续数学。
2、计算机图形学第一准则:近似原则 。如果它看上去是对的,它就是对的。
3、常见坐标系。
1)世界坐标系。
2)物体坐标系。
3)摄像机坐标系。
4)惯性坐标系。
4、向量的大小。

5、点积:对应分量的和。
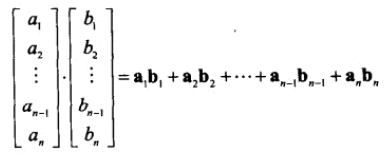
点积可以计算向量的夹角:

6、假设有向量v,n,则v可以拆分平行为n的向量 v1、以及垂直于n的向量v2。

v1 = |v1|*n / |n| = |v| cos0 *n / |n| = |v||n|cos0*n / |n|^2 = dot(v,n)*n/|n|^2

上术计算 v1 的公式,可以略去 cos0 的计算。
有了v1,v2就很好求了。 v2 = v - v1

7、叉乘公式。

叉乘不满足交换律,即: axb != bxa。但满足反交换律:

也不满足结合律:

叉乘满足分配律:
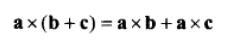
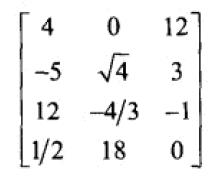
8、矩阵是 row x column,如下面是一个 4x3 的矩阵。
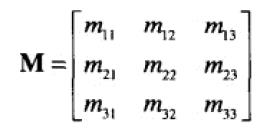
9、两个矩阵积的转置 等于 转置的逆序积。

10、行向量左乘矩阵,结果是行向量;行向量右乘矩阵,结果是无定义。
列向量左乘矩阵,结果是无定义;列向量右乘矩阵,结果是列矩阵。
并且注意,行向量、列向量的值完全不同。

11、若把矩阵的行解释为基向量,那么乘以该矩阵就相当于执行了一次坐标转换。若有 aM = b,我们就可以说,M可以将a转换到b。


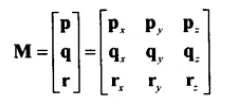
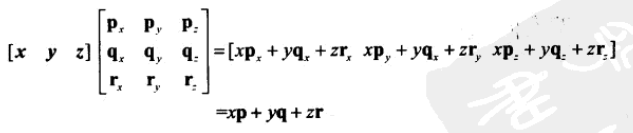
12、绕x、y、z 轴旋转 0度。



记法诀窍:
1、斜角都是 cos0。
2、固定轴的下一个是 sin0。
3、固定轴的下下一个是 -sin0。
13、沿坐标轴的绽放矩阵。
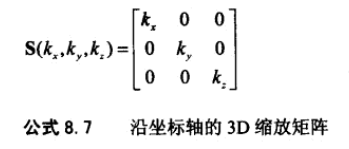
14、切变,切变后面积、体积不变。也被称作扭曲变换。以下是 2d切变矩阵:
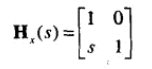
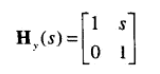
以下是3D切变矩阵。
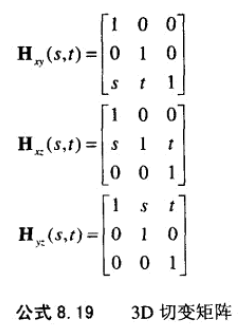
15、线性变换。满足加法、线性乘,那么叫线性变换。
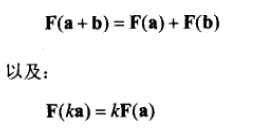
16、2 维行列式

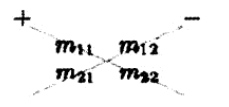
3维行列式:


如果将矩阵解释为 abc 向量,那么矩阵的行列式可以写为:

17、M{i,j} 称为 M的i行j列的余子式,意为去除i行j列后余下的矩阵。
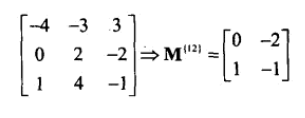
加上-/+后称为代数余子式。

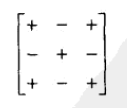
任一一行的代数余子式与元素乘积的和,即为行列式,所以这里得到行列式的另一个计算方法:


18、矩阵行列式的特性。

19、2D中,行列式的值为基向量围成图形的面积。
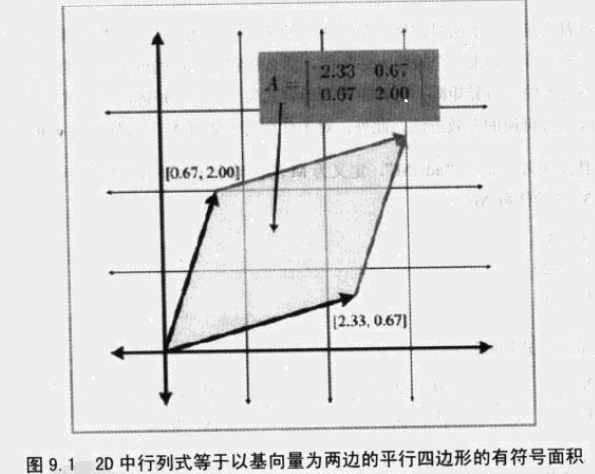
3D中,行列式等于基向量的体积。
20、如果一个矩阵有逆矩阵,则称它为可逆的或非奇异的(非单身)。如果没有逆矩阵,则为不可逆,奇异。
奇异矩阵的行列式为零,非奇异的行列式不为零。因为逆矩阵的计算需要除以行列式 |M|。
21、adj M 是标准伴随矩阵,是代数余子式矩阵的转置。
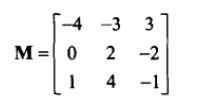


逆矩阵的计算公式:
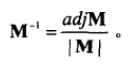
逆矩阵的特性:


22、正交矩阵:M*M^T=I
如果一个矩阵是正交的,那么它的转置等于它的逆: M^-1 = M^T。
这是快速计算逆矩阵的一种常用方法。
23、正交矩阵性质的推导。
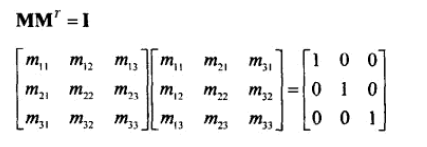

23.1、3D矩阵的施密特正交化。
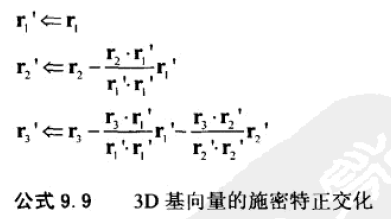
施密特正交化是有偏差的,一个例子是rq总是不变的。一个改进的算法是,选择一个小因子,迭代N次。
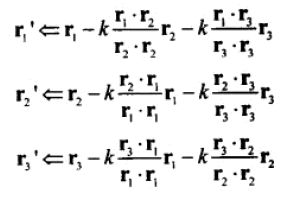
24、3D 平移矩阵。

24.1、一般仿射变换。
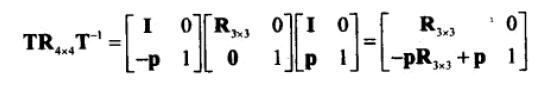
25、投影的计算。


26、
27、
28、
29、
【3D中绕任意轴的旋转】
假设旋转轴通过原点,为n,旋转的角度为0。被旋转轴为 v,旋转后的轴为 v'。则我们需要找到的旋转矩阵R为:

先构造空间,可以将 v 拆分为 v1、v2,v1平行n,v2垂直n。

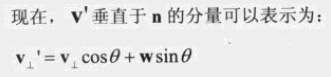
下面的等式可由两种方式得到:
1)0 的旋转矩阵。
2)水平分量、垂直分量相加。
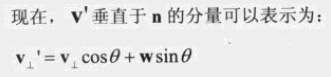


将 [1,0,0]、[0,1,0]、[0,0,1] 代入,即可得三个旋转后的坐标轴。

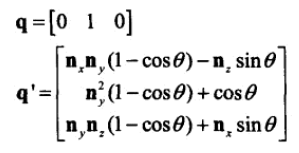
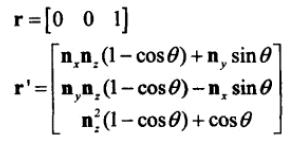
综合在一起,可得旋转矩阵:

【沿任意方向缩放】
现在来解决,沿方向n,绽放k倍的问题。假设需要绽放轴 v,那么v可拆分为v1,v2。v1平行于 n,v2 垂直于n。

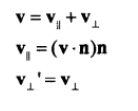
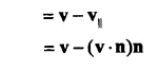
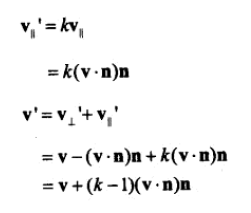
上式中,(VN)N 为 V||,再乘上 (k-1),所以此公式的含意为给 V 加一个 (k-1)V|| 的偏移。
所以,三个轴旋转后分别为:


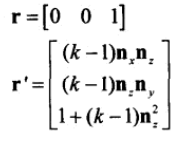
绽放矩阵为:

有了上述公式后,可轻易的得出绕任意平面投影的矩阵:

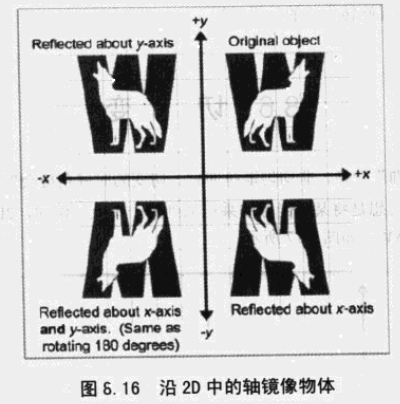
同样,镜像矩阵也很容易得出: