Cyclomatic Complexity
1. 概念
a. 圈复杂度是一种衡量代码复杂程度的标准。
b. 圈复杂度高的害处:
圈复杂度大说明代码的判断逻辑复杂,可能质量低;
需要的更多的测试用例,难于测试和维护;
程序的可能错误和高的圈复杂度有着很大关系。
c. 圈复杂度的表现:
代码中分支循环语句多(if/else, switch/case, for, while),圈复杂度与分支循环语句个数正相关;
表达式复杂(含有三元运算符 )。
2. 圈复杂度的计算方法
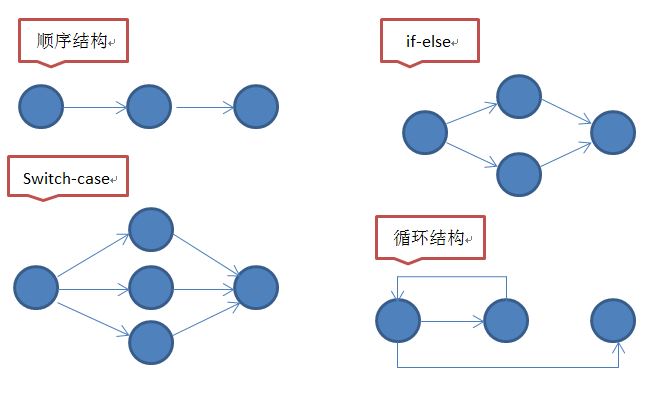
(1)圈复杂度可以通过程序控制流图计算,公式为:V(G) = e + 2 - n
e : 控制流图中边的数量
n : 控制流图中节点的数量(包括起点和终点;所有终点只计算一次,多个return和throw算作一个节点)
(2)圈复杂度对应程序控制流图中从起点到所有终点的路径的条数,所以页可以通过数路径的方式获得圈复杂度。
3. 圈复杂度计算实例
private int CalculateScore(int culture, String nation, boolean extend) { int result = 0; if (culture < 0) { throw new RuntimeException("分数不能小于0"); } else if (culture < 200) { return culture; } else { switch (nation){ case "汉": result = 0; break; case "蒙": case "回": case "维": case "藏": result = 10; break; default: result = 20; } } if (extend) { result += 10; } return result + culture; }
程序控制流图:
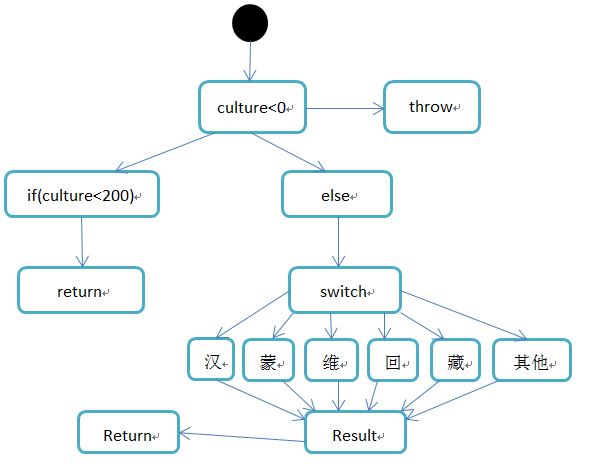
(1) V(G) = 21 + 2 - 13 = 8;
(2) 数路径:8条
4. 减小圈复杂度的方法
a. 提取函数 - 将独立业务或模块代码独立出来,封装为函数,通过函数名诠释代码作用,做到见名知意。
b. 替换算法 - 复杂算法会导致bug可能性的增加及可理解性/可维护性的降低,如果函数对性能要求不高,提倡使用简单明了的算法。
c. 分解条件式 - 复杂的条件表达式,使用函数进行封装
d. 合并条件式 - 将一系列得到相同结果的条件表达式合并,可以的话封装为函数
e. 合并重复的条件片段 - 不同条件的分支,有相同的处理,可以提炼出分支以外,或者封装为函数
f. 移除控制标记 - 使用控制标签作为条件的,使用break 和 return取代
g. 将查询函数和修改函数分离 - 单一职责原则,强调函数的复用性而不是多用性
h. 函数携带参数 - 使用带参函数,强调函数的复用性
i. 以明确函数取代参数 - 强调函数的功能的明确性