摘要
本文研究了条件极大似然估计的渐近性质和基于似然的弱外生性检验。I（2）VAR模型中的弱外生性允许我们基于混合高斯分布进行渐近条件推断。I（2）VAR中弱外生性的对数似然比检验统计量模型是渐近χ 2分布。本文还介绍了使用日本宏观经济数据提出的弱外生性测试的实证说明。
引言
本文的主要目标是：（i）研究向量自回归（VAR）模型中弱外生性的似然性分析的极限理论，其中变量积分为二阶（表示为I（2）），（ii）给出I（2）VAR分析的经验说明，该分析以弱外生性的基于似然的检验为中心。诸如线性趋势之类的确定性术语通常在宏观经济数据的经验建模中起关键作用。因此，线性趋势和常数都包含在模型中。本介绍部分首先概述了关于弱外生性和I（2）协整分析的文献，然后描述了本文的最重要方面。
模型和表示
让我们考虑一个p维时间序列的VAR（k）模型是根据初始值X 0，...，X - k制定的，如下所示：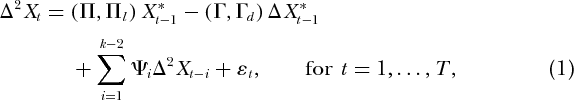
蒙特卡洛实验
本节进行蒙特卡罗实验，测试I（2）协整VAR系统中的弱外生性。实验的目的是揭示两种测试的有限样本属性，即上面讨论的log LR测试和基于Paruolo和Rahbek的两步过程的测试。数据生成过程（DGP）的基线设置作为X t =（X1， t，X2， t，X3， t）'的三变量系统给出，并规定如下：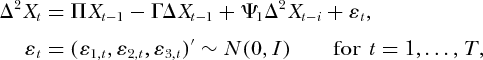
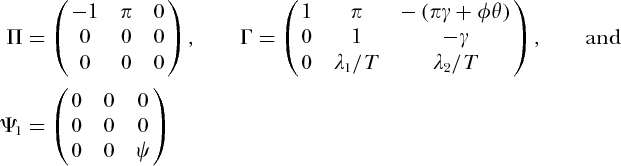和θ= 1 +γ 2（1 +π 2）≠0。在DGP积分指数用（给出ř，小号）=（1，1），和长期运行参数β和它的正交补β 1和β 2由（定义2）是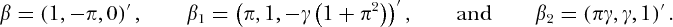
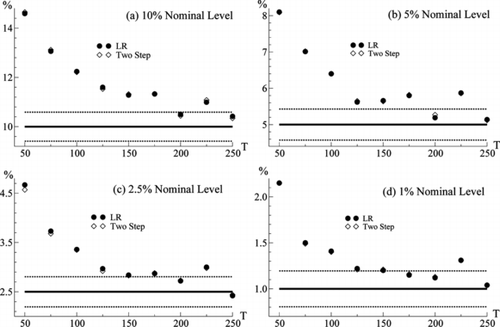
在该图中，所有观察到的尺寸变形趋于随着T的增加而减小，并且基于两个测试统计的拒绝率之间几乎没有差异。因此，实验表明，两种测试统计数据都可能具有相似的有限样本大小属性。
图1拒绝频率的递归图。
同样，该图表明，在功率方面，log LR测试统计优于基于两步的测试统计。
图2尺寸调整的功率函数。
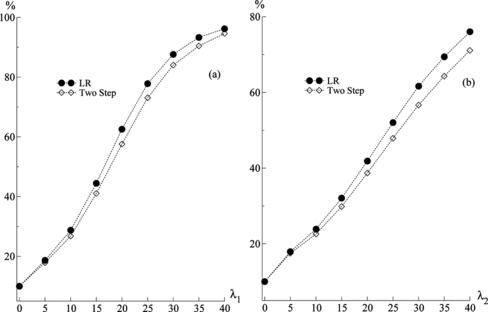
因此，实验结果可能允许我们推测log LR检验统计量可能比基于两步估计程序的统计量更强大，尽管两个检验统计量的大小属性似乎几乎相同。这些模拟研究为两个测试统计数据的有限样本属性提供了有用的信息，但需要进一步调查才能在这个问题上得出决定性的结论。除了这些模拟结果之外，两步程序基本上是最大似然的近似这一事实也可能有助于证明在实证研究中更加重视对数 LR检验。
日本宏观经济概述
实证分析从一般的无限制VAR（5）模型开始，该模型包含两个确定性项，即常数和线性趋势。样本期从1976年的第二季度到2000年的最后一个季度。有关数据的详细信息，请参阅附录。滞后5处的所有变量都被消除，但是从滞后4到3的减少被F检验拒绝。因此，协整分析的初始模型是滞后长度为4 的VAR模型，估计的观测数量为98。
结束语
本文研究了I（2）VAR模型中弱外生性可能性分析的渐近理论，并对I（2）数据进行了实证分析，该数据集中在弱外生性的基于似然的检验上。诸如线性趋势之类的确定性术语通常在宏观经济数据的经验建模中起关键作用。因此，线性趋势和常数都包含在模型中。