R语言Bootstrap、百分位Bootstrap法抽样参数估计置信区间分析通勤时间

全文链接：http://tecdat.cn/?p=27505

原文出处：拓端数据部落公众号

y本文展示了如何使用 R 构建Bootstrap自举置信区间的示例。还强调了 R 包 ggplot2 用于图形的用途。但是，在学习引导程序和 R 语言时，学习如何在没有包的情况下从头开始应用Bootstrap程序有助于更好地理解 R 的工作原理并加强对Bootstrap的概念理解。

 相关视频：什么是Bootstrap自抽样及应用R语言线性回归预测置信区间实例

什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间

，时长05:38

具有标准误差的自举置信区间
 

描述了如何通过构建一个以点估计为中心的区间来构建总体参数的置信区间，其误差幅度等于标准误差的两倍。在这里，我们将通过应用 bootstrap 并从原始样本中对许多样本进行带放回抽样来估计标准误差的大小，每个样本与原始样本的大小相同，计算每个样本的点估计值，并找到该分布的标准差引导统计。

通勤时间

关于 500 名通勤者样本的变量。
 

1.  
    
2.  
   str(Cotlaa)

为了构建平均通勤时间的置信区间，我们需要从原始样本中找到点估计（样本均值）。
 

1.  
   tiean = with(Commta, mean(Time))
2.  
   tiean
3.  
   ## [1] 29.11

为了找到标准误差，我们将创建一个包含 1000 行（每个引导样本一个）和 500 列（每个采样值一个，以匹配原始样本大小）的巨大矩阵。然后我们将使用 apply() 将 mean() 应用于矩阵的每一行。这种方法不同于作者 R 指南中使用 for 循环的示例，但我们也可以稍后展示这种方法。
首先创建一个大矩阵来存储所有样本。
 

1.  
    
2.  
   boot.ames = matrix(sale(Comnta$Tie, size = B * n, replace = TRUE),
3.  
   B, n)

用密度图覆盖直方图来绘制不同的东西。在这里，ggplot() 需要一个带有输入数据的数据框，因此我们使用 data.frame() 创建一个带有唯一感兴趣的变量的数据框
 

1.  
   require(ggplot2)
2.  
   ggplot(dtframeanT = boot.satitics),as(x=meaime)) +
3.  
   geom_istram(binwih=0.25,aes(y=..ensity..)) +
4.  
   geodnity(olor"red")

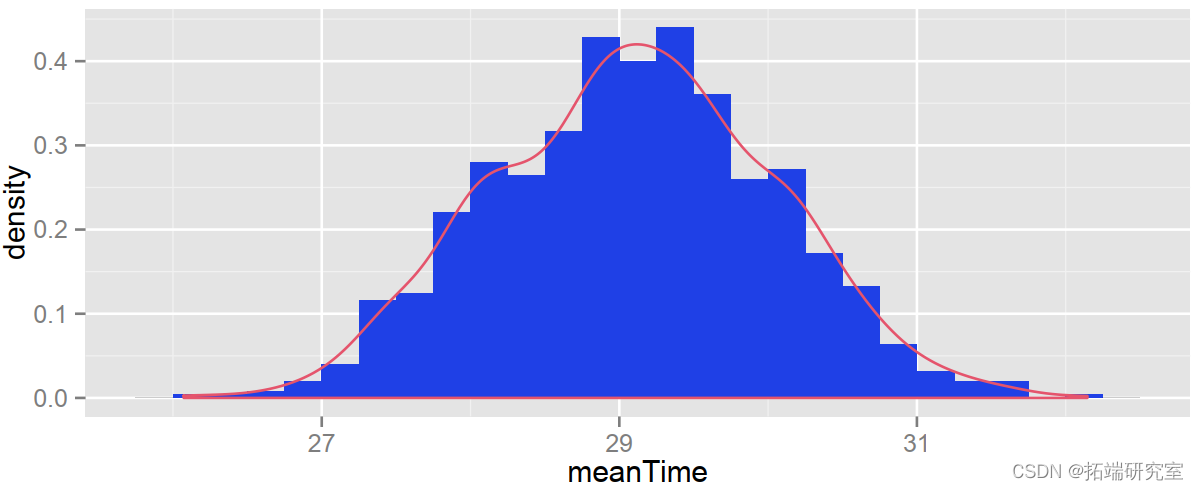
我们看到了一个不太不对称的分布，或多或少呈钟形。该分布的标准差如下
 

1.  
   tie.s= sd(bo.sattics)
2.  
   tie.s
3.  
   ## [1] 0.9414

最后，构建置信区间。在这里，我将误差范围向上舍入到小数点后一位，使其具有两位有效数字，并且在四舍五入时要小心不要使间隔太小。

1.  
   me= cilig(10 * 2 * tim.se)/10
2.  
   rond(tme.an, 1) + c(-1, 1) * me
3.  
   ## [1] 27.2 31.0

现在在上下文中解释。
我们有 95% 的信心认为，不在家工作的通勤者在平均通勤时间在 27.2 到 31 分钟之间。

编写函数
 

由于有几个复杂的步骤，所以有一个函数来完成所有这些步骤会很有用，这样将来我们可以在函数中获取源代码，然后调用它。这是一个示例函数，它接受一个参数 x，该参数假定为一个数字样本并执行 B 次引导。该函数会将有用的信息输出到控制台，绘制分布图，并以列表的形式返回统计、区间、标准误差和图表。
 

1.  
    
2.  
   out= with(tdens botmean(eit))

1.  
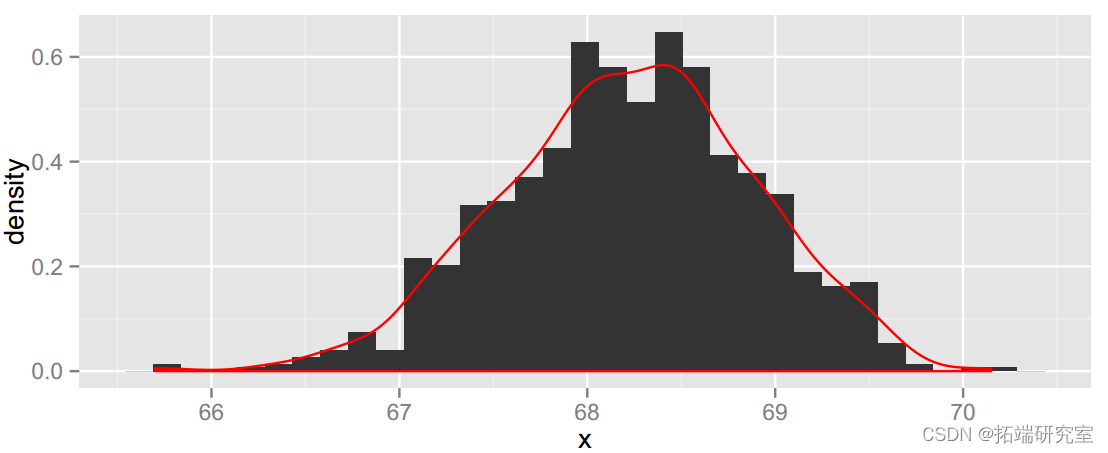
   ## [1] 66.90 69.56
2.  
   out$interval
3.  
   ## [1] 66.90 69.56

我们需要谨慎，因为学生样本不是随机的，而是我们班的方便样本。这里有两个可能的混淆变量：性别和原籍国。

for 循环

for 循环不是一次采集所有样本，而是一次采集一个样本。通常，使用 apply() 的 R 代码比使用 for 循环的代码更有效。尝试大量的 bootstrap 复制！

1.  
   n = ngth(studentseiht)
2.  
   B = 100
3.  
   reslt = re(NA, )
4.  
   fo(i in 1:) f
5.  
   bo.sale= smpe(, replace = TRUE)
6.  
   reult[i] mean(udetsHeht[bot.mple])
7.  
    
8.  
   with(stdnt, men(Hit) + c(-1, 1) * 2 * sd(result))
9.  
   ## [1] 66.89 69.58

比例
 

考虑估计橙色里斯糖果的比例问题。选择了一个有 11 个橙色糖果和 19 个非橙色糖果的学生。让我们使用 bootstrap 找到橙色 Reese 比例的 95% 置信区间。最简单的方法是将样本数据表示为具有 11 个 1 和 19 个 0 的向量，并使用与样本均值相同的机器

rees.bot= bot.man(rees, 1000,nwith = 1/30)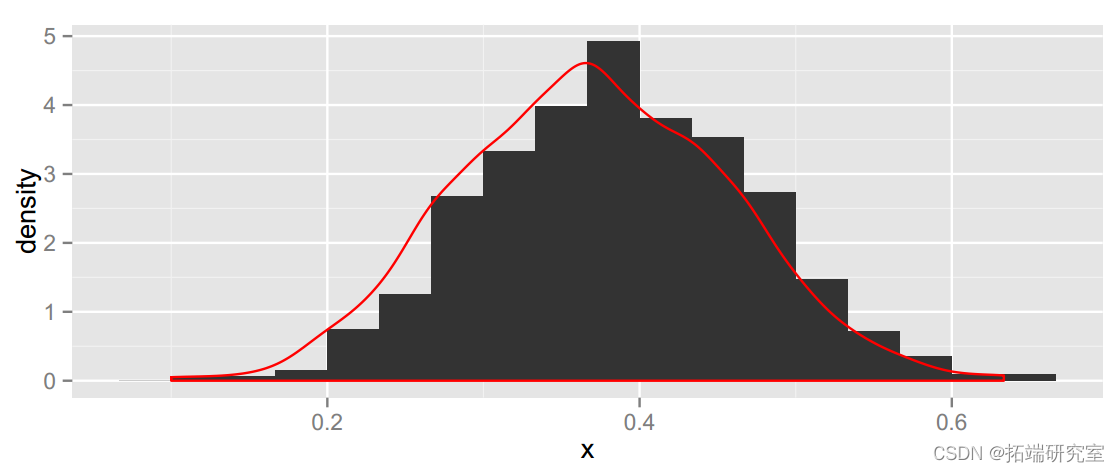

## [1] 0.1947 0.5386

因此，仅基于这个单一样本，我们有 95% 的信心认为橙色的真实比例在 0.19 到 0.54 之间。如果我们将所有 48 个样本组合成一个大样本，我们可以重做这个问题。观察到的比例为 0.515，共有 741 个橙色糖果和 699 个非橙色糖果。

1.  
   reeses = c(rep(1, 741), rep(0, 699))
2.  
   reeses.boot = boot.mean(reeses, 1000, binwidth = 0.005)

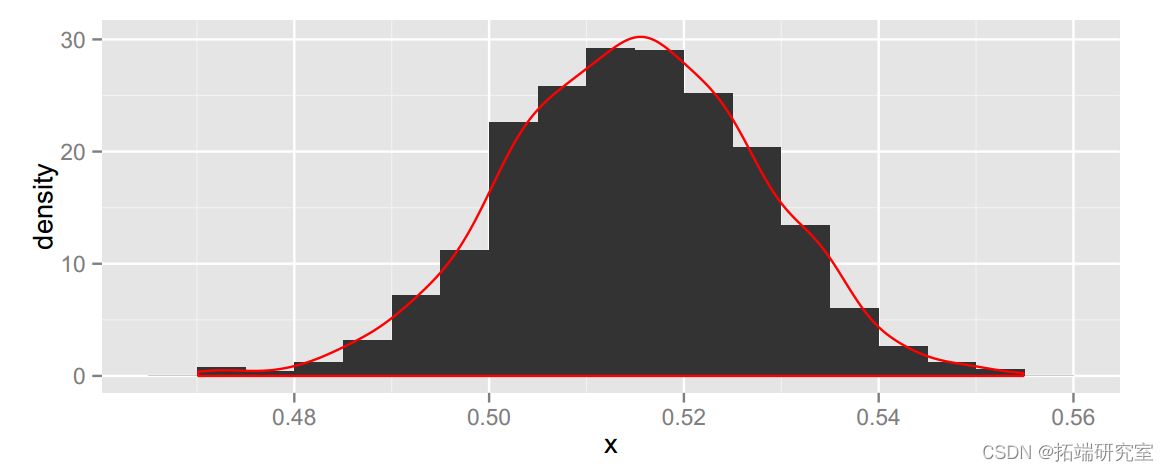
## [1] 0.4888 0.5404

均值差异

我将使用学生调查数据集来说明如何使用 bootstrap 来估计均值的差异。有趣的变量是联系，每周每个学生练习的小时数。

data(Stey)

我们从这个总结中看到，在样本中，男性每周锻炼的时间比女性多。如果我们将此学生样本视为从大学生群体中随机选择的，我们可以估计每种性别的锻炼时间差异。

在构建置信区间之前，这里是两个分布的图表。

1.  
   geom_boxpot(lor=red,ouolor="ed") +
2.  
   geom_oin(poitio osio_jitt(h=0w=0.3)) +

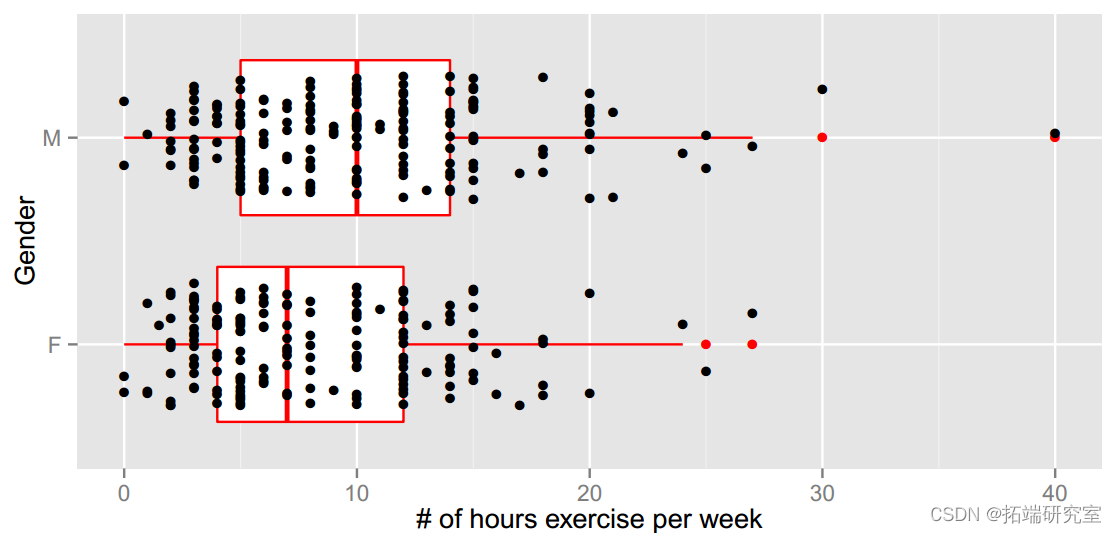
 我们使用 length() 来查找每个组的样本大小。请注意，女性人数为 n[1]，男性人数为 n[2]。

n = withnewSt、nt, by(Ec Gende, lengh))

下一个代码块为样本中的男性和女性创建一个矩阵，每个样本的替换大小相同。然后我们使用 apply() 来微调每个样本的平均值并取差值（男性减去女性）来获得统计的分布。我们用图表来检查对称性。

1.  
    
2.  
   ggplot(data.amex = oot.at), aes( = x)) + ge_ensty()

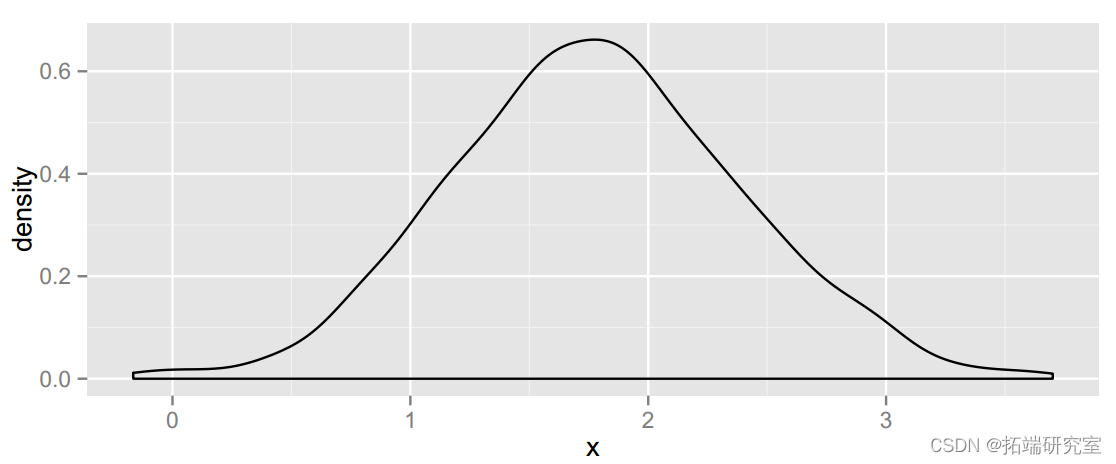
 最后，取点估计（样本均值的差异）并加上和减去两倍的标准误差。查看未四舍五入的版本后，将两位有效数字四舍五入到小数点后一位。

boot包

有一个带有函数 boot() 的包 boot，它在许多情况下都可以进行boottrap。我将重温通勤时报的例子。

但是内置函数 boot.ci() 将使用多种方法计算 bootstrap confidenceintervals。

boot.ci(t.boot)

基本使用估计的标准误差。百分位数使用百分位数。BCa 也使用百分位数，但会根据偏差和偏度进行调整。

百分位bootstrap

使用来自 bootstrap 的百分位数的置信区间的想法是从 bootstrap 分布的中间选择与所需置信水平相对应的端点。
 

1.  
    
2.  
   for ( i in 1:B ) f
3.  
   te.boot] = meanmplta,size=tea.neplTRU)
4.  
   cofeebot[i] = eanampe(ffee,ize=cen,repla=TRUE)
5.  
   g
6.  
    
7.  
   quatil(bot.tt0.025,0.975))
8.  
   quantie(boottac(0.005,0.995))
9.  
    

 

自测题

Below are some 1973 law school data, mean GPA and mean LSAT score for N=82 law schools. Compute approximate 95% CIs by bootstrapping for: (a) the mean GPA mean; (b) the mean LSAT mean; (c) the correlation between GPA mean and LSAT mean, at the school level.  Do all of these calculations for a sample of size n=15, and then repeat for a sample of size n=20. Note that you'll get somewhat different answers for different choices of sample, for each size (15 and 20). You can explore the importance of the particular sample chosen, of course, by repeating the process. Be careful not to conflate the bootstrap process and the repetition of sampling from the "population."  In a typical boostrap computation, you would have only a sample of size 15 (or 20) and not the "population" of 82, and the boostrap procedure does not require that you have the 82 data points (or it wouldn't be very helpful).

---

最受欢迎的见解

1.使用R语言进行METROPLIS-IN-GIBBS采样和MCMC运行

2.R语言中的Stan概率编程MCMC采样的贝叶斯模型

3.R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样

4.R语言BUGS JAGS贝叶斯分析 马尔科夫链蒙特卡洛方法（MCMC）采样

5.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

6.R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

7.R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数

8.R语言使用Metropolis- Hasting抽样算法进行逻辑回归

9.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长