Matlab用向量误差修正VECM模型蒙特卡洛Monte Carlo预测债券利率时间序列和MMSE 预测

原文链接：http://tecdat.cn/?p=27246 

原文出处：拓端数据部落公众号

此示例说明如何从 VEC( q ) 模型生成 Monte Carlo 预测。该示例将生成的预测与最小均方误差 (MMSE) 预测和来自VEC( q ) 模型的 VAR( q +1) 模型的预测进行比较。

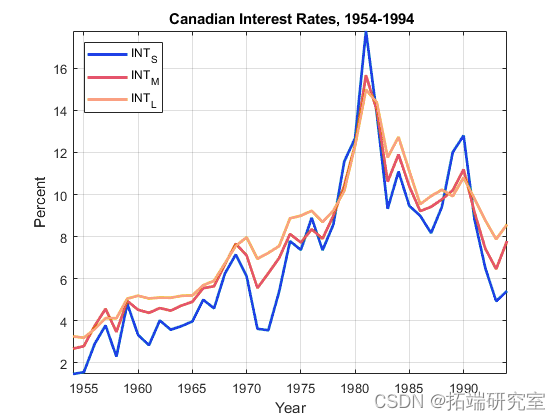
假设具有 H1 Johansen 形式的 VEC(2) 模型恰当地描述了由 1954 年至 1994 年的年度短期、中期和长期债券利率组成的 3D 多元时间序列的动态。

加载和预处理数据

加载 数据集。

1.  
    
2.  
   Td = size(Ya,1)

 

numSdsrfiess = size(sY,2)

 

在同一图中绘制序列。

1.  
    
2.  
   plot(dastdes,Y,'LineadaassWidth',2)
3.  
   xlabel 'Yeasdar';
4.  
   ylabel 'Perasdacent';
5.  
   legend(ndaamsess,'Lodcatsion','NW')

估计 VEC 模型

创建协整等级为 2 的 3D VEC(2) 模型。

1.  
   nuassdamLags = 2;
2.  
   ras = 2;
3.  
   Maddl = vecasm(nuassmSeriaes,dasr,asdnuamLsags);

估计 VEC(2) 模型。

EssasdtMasl = esastimdate(Masddl,Yas);

默认情况下， estimate 应用 H1 Johansen 形式并使用前 q  + 1 = 3 个观测值作为预采样数据。

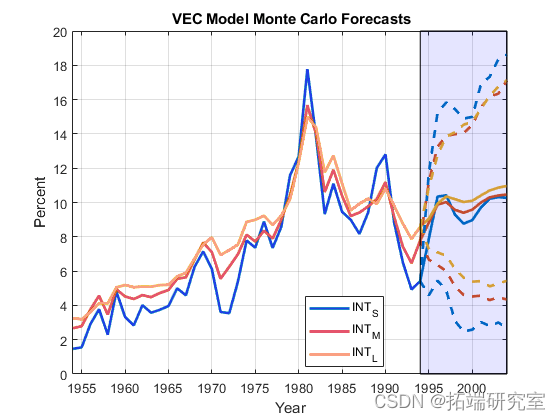
生成蒙特卡洛预测

使用 . 从估计的 VEC 模型生成 10 年的蒙特卡罗预测 simulate。提供最新的三行数据来初始化预测，并指定生成 1000 条路径。

1.  
   numaPaddtfhs = 1000;
2.  
   hsoriszosn = 10;
3.  
   Y0sa = Y((enssdd-2):enad,:);
4.  
    
5.  
   aYSisasddmVaEC = simausdlate(EstasdaMdl,hoasdrizon,'NumPatahs',numPdathas,'Y0d',Y0a);

估计所有路径上每个时期和时间序列的预测均值。为每个时期和时间序列构建 95% 的百分位预测区间。

1.  
   YMCsdfVsdEC = meafn(YSidmdfggVEC,3);
2.  
   YMCfVECdsCIf = quandftile(YSdfgdfimVgdfEC,[0.025,0.975],3);

绘制有效样本观测值、平均预测值和 95% 百分位置信区间。

1.  
   fDdatesf = dsatdfes(end) + (0:horsdizfon)';
2.  
   figure;
3.  
   h1f = plddot([fdatsdes; fDfatesds(f2:end)]sd,[Y; YMCVEC],'LineWidth',2);
4.  
   hds2 = fsgcsda;
5.  
   hold on
6.  
   h3 = plsdot(frepmsdat(ffsdDatdes,1,3),[Y(endfsd,:,:); YMCVEsddfCCI(:,:,1)],'--',...
7.  
   'LineWidtdsdsh',2);

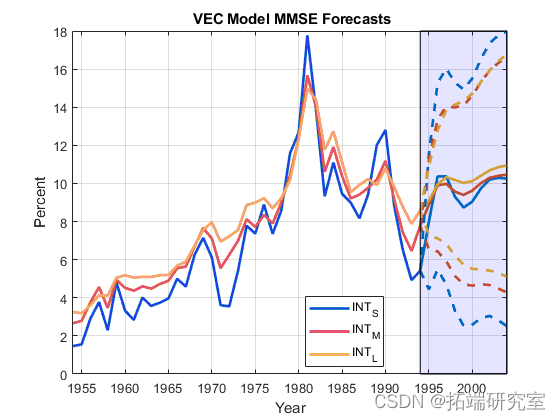
生成 MMSE 预测

使用估计的 VEC 模型在 10 年的范围内估计 MMSE 预测 forecast。提供最新的三行数据来初始化预测。返回预测和相应的多元均方误差。

[YMaMSaE,YMMsSgEfMSE] = forecast(EssstfMddl,horsgizfson,Y0);

YMMSE 是 MMSE 预测的 10×3 数值矩阵。行对应于预测范围内的期间，列对应于 中的序列 Y。 YMMSEMSE 是 3×3 数值矩阵的 10×1 元胞向量。单元格 j中的矩阵是周期j 中三个预测值的估计多元 MSE  。矩阵的对角线值是预测 MSE，以及预测协方差的非对角线值。

估计 Wald 类型的 95% 预测区间。绘制 MMSE 预测和预测区间。

1.  
    
2.  
   hs1 = plsdot([datsdfes; fdDgsategs(2:ednd)],[Y; YsdfMMSEf],'LinseWdsdfidth',2);
3.  
   dfh2 = gca;
4.  
   hold on

VAR( q  + 1) 表示 MMSE 预测

将估计的 VEC(2) 表示为 VAR(3) 模型。

EstsdMdsdfldVAfdR = vafrm(EssdfdtMsdl)

 

 使用 VAR 模型估计 10 年的 MMSE 预测 forecast。提供最新的三行数据来初始化预测。返回预测和相应的多元均方误差。

[YMMsdSEVAR,YMMsdSEfMasdSEVAR] = foresdfcast(EsstfMdlVdAR,horiddzson,fY0);

估计 Wald 类型的 95% 预测区间。绘制 MMSE 预测和预测区间。

1.  
   YMMfSEVsAdfRCI = zeros(hsdrifzon,nusfdmfSesdrsdies,2);
2.  
   YMMSEMdSEsdVsAR = cell2fsdfmat(cellfun(@(x)diag(x)',YMMSEMSEVAR,'UniformOusdftput',false));
3.  
   YMMSEVARCI(:,:,1) = YMMSE - 1.96*sqrt(YMMSEsdsdffMSEVAR);
4.  
   YMdMSfEdfVARCI(:,:,2) = YMMSE + 1.96*sqrt(YMMSEMfSEdsVAR);
5.  
    
6.  
   figsdfure;
7.  
   h1 = plot([datdfses; fDatses(2:engd)],[Yd YMMhfSEgf],'LingheWidth',2);

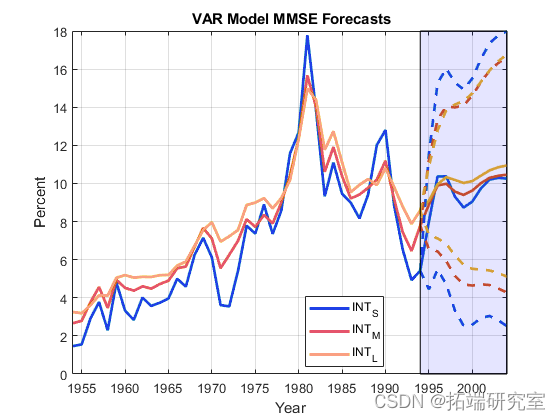
确认来自 VEC 和 VAR 模型的 MMSE 预测是相同的。

(YqwMeMSE - YMMSEVweAR)'*(YMMwSE - YMretMSyEVAR) > ertps

模型之间的 MMSE 预测是相同的。

---

最受欢迎的见解

1.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

2.R语言改进的股票配对交易策略分析SPY—TLT组合和中国股市投资组合

3.R语言时间序列：ARIMA GARCH模型的交易策略在外汇市场预测应用

4.TMA三均线期指高频交易策略的R语言实现

5.r语言多均线量化策略回测比较

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model

9.matlab使用Copula仿真优化市场风险