原文链接：http://tecdat.cn/?p=25860
原文出处：拓端数据部落公众号
什么是尾部相关性？假设市场出现了属于最差 5% 的日子的回撤：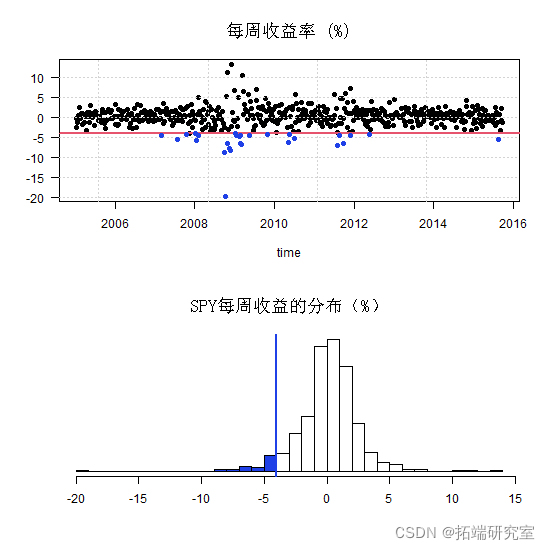
有人可以问，鉴于市场处于蓝色区域，特定股票下跌的概率是多少？
我们都了解股票相对于市场的贝塔系数、股票相对于市场的敏感性（例如标准普尔 500 指数）的概念。尾部相关性的概念类似，因为它是股票对市场回撤的敏感性。如果每次市场下跌，股票下跌，那将意味着两件事：
1. 鉴于市场已经下跌，股票下跌的概率是 100%。
2. 股票对市场下跌非常敏感
直观地认为，这样的方法会与高beta 值相伴而行。但这并不是一对一的。很有可能的是，与另一只低beta 的股票相比，高beta 的股票对下跌的敏感度较低。
形式上，股票左尾对市场左尾的相关性定义为：
(1) 
其中 Q 是分位数，这取决于您如何定义尾部，在我们的示例中为 5%。从概率来看，如果两个事件是独立的，那么看到这两个事件的概率是每个事件概率的乘积：
(2) 
其中 A 是事件： 
, B 是事件 
。根据经验，我们所做的估计只是简单地计算位于股票 5% 临界值以下的点数，对于位于市场 5% 以下的每个点。这个函数使用这个概念来衡量两个时间序列之间的尾部相关性：
-
# cc参数定义了尾部。默认为5%。
-
-
co<- function{
-
-
# 如果两个序列不在同一长度上，则停止。
-
-
if(length!=length(sb)){stop }
-
-
TT <- length(
-
-
-
-
# 计算有多少是低于5%的
-
-
ind0 <- ifelse
-
ind <- which
-
-
# 鉴于序列a低于5%（意味着有缩减），计算序列b中有多少个
-
-
ind1 <- sum(ifelse(reb<quantile,1,0))
-
-
# 计算概率
-
-
p0 <- id1/TT # 两者都放弃的概率
-
让我们拉出 10 只 ETF，看看 beta 与尾部相关性度量有何不同。我们拉动股票代码并转换为每周收益。
-
-
sym
-
l=length
-
end
-
dat0 = (getSymbols
-
n = NROW
-
-
w0 <- NULL
-
-
for (i in 1:l){
-
-
dat0 = getSymbols
-
w1 <- weeklyReturn
-
w0 <- cbind
-
}
现在我们计算 beta 和尾部相关性度量，并绘制它。
-
pr <- bet <- NULL
-
-
for(i in 1:(l-1)){
-
-
bet[i] <- lm
-
pr[i] <- cortr
-
}
-
-
barplot
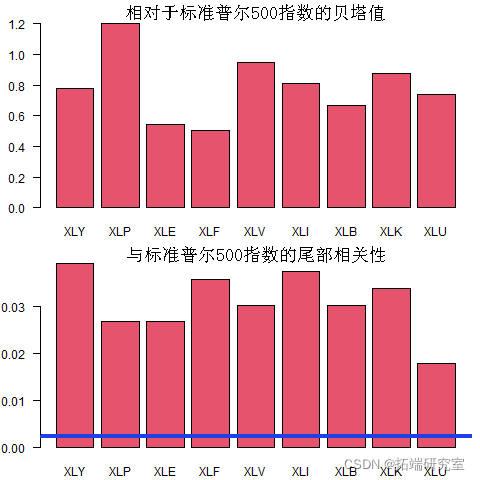
蓝线是 
这是我们对两个完全（尾部）独立序列的期望。
用简单的计量经济学对尾部相关性建模，可以考虑使用回归设置。使用无截距回归同样可以达到第二张图表的底部面板：
(3) 
其中， 
是事件 A 发生时股票出现回撤的指标函数。看一看：
-
fiquan <- quantile
-
indl <- ifelse
-
betdpe <- NULL
-
-
for(i in 1:(l-1)){
-
-
fivuan <- quantile
-
indk <- ifelse
-
betence[i] <- lm$coef[1]
-
-
}
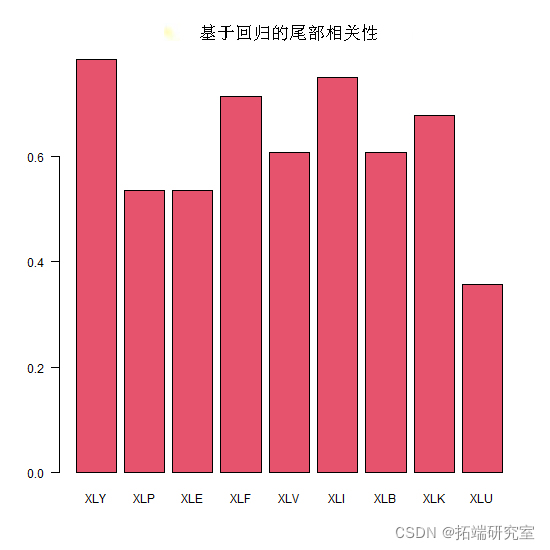
因此，我们可以使用我们对回归的了解并将分析扩展到多变量案例，而不是使用困难的多维 copula 和收敛问题。在不仅有B的缩减，而且有C和D的缩减的情况下，我们看到A的缩减有多大可能。
不足和展望
– 我们可以进行推断，但不使用回归系数的通常 STD，因为它是指标回归.
– 我们还必须包括交互项，以使推理有效。
– 我们用更新的回归方法来改进估计；套索lasso、bagging等
最后，我想知道 XLU（公用事业）ETF 的情况如何，为什么尾部相关性相对于 beta 而言看起来很弱，以及与 XLY（消费者自由裁量权）相比，情况有何不同。
-
-
plot
-
lines(lowess, lwd = 2, col = 4)
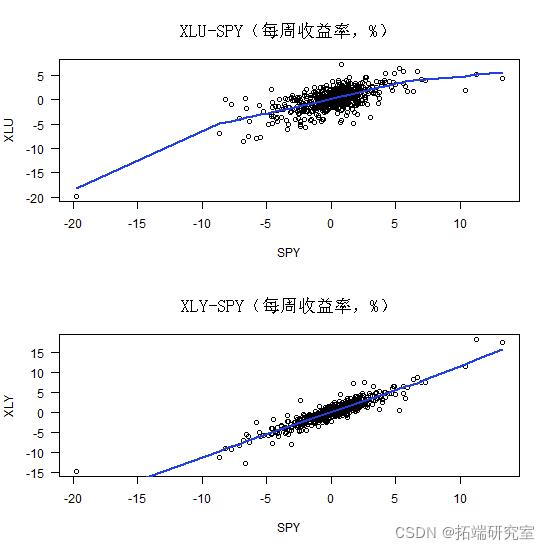
我们的估计对一些极端观察很敏感。也许稳健的回归会提供更稳定的估计，因此这是另一个可能的扩展。
最受欢迎的见解
3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）
5.R语言回归中的Hosmer-Lemeshow拟合优度检验