原文链接:http://tecdat.cn/?p=24148
原文出处:拓端数据部落公众号
特别是在经济学/计量经济学中,建模者不相信他们的模型能反映现实。比如:收益率曲线并不遵循三因素的Nelson-Siegel模型,股票与其相关因素之间的关系并不是线性的,波动率也不遵循Garch(1,1)过程,或者Garch(?,?)。我们只是试图为我们看到的现象找到一个合适的描述。
模型的发展往往不是由我们的理解决定的,而是由新的数据的到来决定的,这些数据并不适合现有的看法。有些人甚至可以说,现实没有基本的模型(或数据生成过程)。正如汉森在《计量经济学模型选择的挑战》中写道。
“模型应该被视为近似值,计量经济学理论应该认真对待这一点”
所有的理论都自然而然地遵循 "如果这是一个过程,那么我们就显示出对真实参数的收敛性 "的思路。收敛性很重要,但这是一个很大的假设。无论是否存在这样的过程,这样的真实模型,我们都不知道它是什么。同样,特别是在社会科学领域,即使有一个真正的GDP,你可以认为它是可变的。
这种讨论引起了模型的组合,或者预测未来的组合。如果我们不知道潜在的真相,结合不同的选择,或不同的建模方法可能会产生更好的结果。
模型平均
让我们使用 3 种不同的模型对时间序列数据进行预测。简单回归 (OLS)、提升树和随机森林。一旦获得了三个预测,我们就可以对它们进行平均。
-
# 加载代码运行所需的软件包。如果你缺少任何软件包,先安装。
-
-
tem <- lappy(c("randomoest", "gb", "quanteg"), librry, charter.oly=T)
-
-
-
# 回归模型。
-
-
-
-
-
-
moelm <- lm(y~x1+x2, data=f)
-
-
-
molrf <- ranmFrst(y~x1+x2, dta=df)
-
-
mogm <- gb(ata=df, g.x=1:2, b.y=4
-
faiy = "gssian", tre.comle = 5, eain.rate = 0.01, bg.fratn = 0.5)
-
-
-
-
# 现在我们对样本外的预测。
-
-
#-------------------------------
-
-
Tt_ofsamp <- 500
-
-
-
boosf <- pbot(df_new$x1, df_new$x2)
-
-
rfft <- pf(df_new$x1, df_new$x2)
-
-
lmt <- pm(df_new$x1, df_new$x2)
-
-
# 绑定预测
-
-
mtfht <- cbind(bo_hat, f_fat, lm_at)
-
-
# 命名这些列
-
-
c("Boosting", "Random Forest", "OLS")
-
-
# 定义一个预测组合方案。
-
-
-
# 为结果留出空间。
-
-
resls <- st()
-
-
# 最初的30个观测值作为初始窗口
-
-
# 重新估计新的观测值到达
-
-
it_inw = 30
-
-
for(i in 1:leth(A_shes)){
-
A_nw$y, mt_fht,Aeng_hee= A_scmes[i, n_wiow = intwdow )
-
-
-
-
}
-
-
# 该函数输出每个预测平均方案的MSE。
-
-
-
# 让我们检查一下各个方法的MSE是多少。
-
-
atr <- apy(ma_ht, 2, fucon(x) (df_wy - x)^2 )
-
-
apy(ma_er[nitnow:Tou_o_saple, ], 2, fncon(x) 100*( man(x) ) )
-
-

在这种情况下,最准确的方法是提升。但是,在其他一些情况下,根据情况,随机森林会比提升更好。如果我们使用约束最小二乘法,我们可以获得几乎最准确的结果,但这不需要事先选择 Boosting 、Random Forest 方法。继续介绍性讨论,我们只是不知道哪种模型会提供最佳结果以及何时会这样做。
加权平均模型融合预测
![]() 是你的预测变量,
是你的预测变量, ![]() 是时间预测
是时间预测 ![]() ,从方法
,从方法 ![]() , 和
, 和 ![]() 例如OLS,
例如OLS, ![]() 提升树和
提升树和 ![]() 是随机森林。您可以只取预测的平均值:
是随机森林。您可以只取预测的平均值:
![]()
通常,这个简单的平均值表现非常好。
在 OLS 平均中,我们简单地将预测投影到目标上,所得系数用作权重:
![\[\widehat{y}^{combined}_t = \widehat{w}_{0t} + \sum_{i = 1}^3 \widehat{w}_{i,t} \widehat{y}_{它}。\]](https://img-blog.csdnimg.cn/img_convert/4a1f640802eb47dd963b0adb183b51a8.png)
这是相当不稳定的。所有预测都有相同的目标,因此它们很可能是相关的,这使得估计系数变得困难。稳定系数的一个不错的方法是使用约束优化,即您解决最小二乘问题,但在以下约束下:
![\[w_{0t} = 0 \quad \text{and} \quad \sum_{i = 1}^3 w_{it} = 1, \qquad \forall t.\]](https://img-blog.csdnimg.cn/img_convert/c7b02ce29511dc91f94d7616fc3947c3.png)
另一种方法是根据预测的准确程度对预测进行平均化,直到基于一些指标如根MSE。我们反转权重,使更准确的(低RMSE)获得更多权重。
![\[w_{it} = \frac{\left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1}}{ \sum_{i = 1}^3 \left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1} } = \ frac{\frac{1}{RMSE_{i,t}}}{\sum_{i=1}^3\frac{1}{RMSE_{i,t}}}.\]](https://img-blog.csdnimg.cn/img_convert/2ff12247b2e7ed75339140d54512f9a2.png)
您可以绘制各个方法的权重: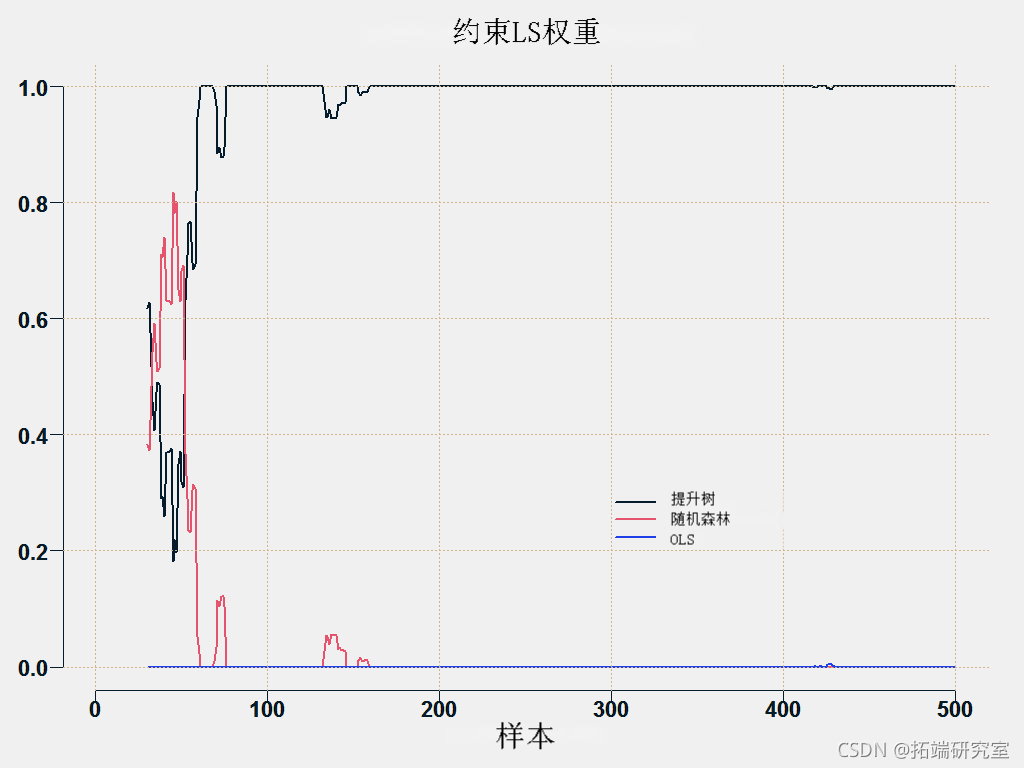
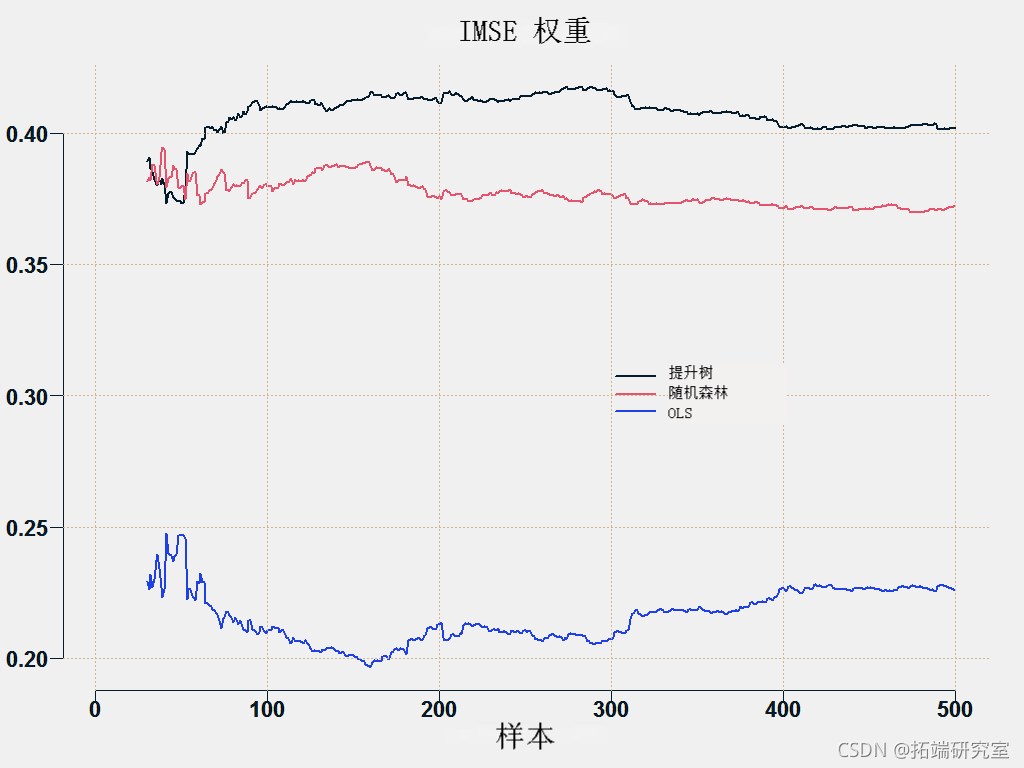
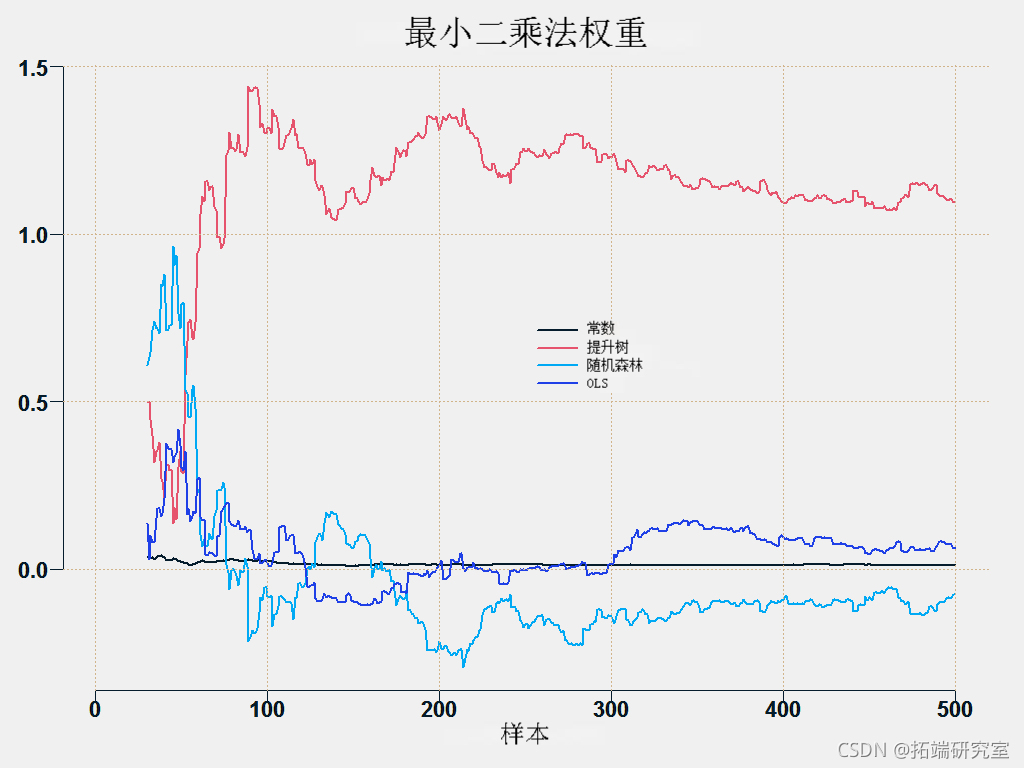
这是预测平均方法。
-
-
-
## 需要的子程序。
-
-
er <- funcion(os, red){ man( (os - ped)^2 ) }
-
-
-
-
## 不同的预测平均方案
-
-
##简单
-
-
-
rd <- aply(a_at, 1, an)
-
-
wehs <- trx( 1/p, now = TT, ncl = p)
-
-
## OLS权重
-
-
-
wgs <- marx( nol=(p+1)T)
-
-
for (i in in_wnow:TT) {
-
-
wghs[i,] <- lm $oef
-
-
pd <- t(eigs[i,])%*%c(1, aht[i,] )
-
-
## 稳健的权重
-
-
-
-
for (i in iitnow:T) {
-
-
whs[i,] <- q(bs[1:(i-1)]~ aft[1:(i-1),] )$cef
-
-
prd[i] <- t(wihs[i,] )*c(1, atfha[i,])
-
-
##基于误差的方差。MSE的倒数
-
-
-
for (i in n_no:TT) {
-
-
mp =aply(aerr[1:(i-1),]^2,2,ean)/um(aply(mter[1:(i-1),]^2,2,man))
-
-
wigs[i,] <- (1/tmp)/sum(1/tep)
-
-
ped[i] <- t(wits[i,] )%*%c(maat[i,] )
-
-
##使用约束最小二乘法
-
-
-
-
for (i in itd:wTT) {
-
-
weht[i,] <- s1(bs[1:(i-1)], a_fat[1:(i-1),] )$wigts
-
-
red[i] <- t(wehs[i,])%*%c(aht[i,] )
-
-
##根据损失的平方函数,挑选出迄今为止表现最好的模型
-
-
-
tmp <- apy(mt_fat[-c(1:iit_wdow),], 2, ser, obs= obs[-c(1:ntwiow)] )
-
-
for (i in it_idw:TT) {
-
-
wghs[i,] <- rp(0,p)
-
-
wihts[i, min(tep)] <- 1
-
-
ped[i] <- t(wiht[i,] )*c(mht[i,] )
-
-
} }
-
-
MSE <- sr(obs= os[-c(1:intiow)], red= red[-c(1:itwiow)])
-
-
-
-

最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析