【拓端tecdat】R语言用Hessian-free 、Nelder-Mead优化方法对数据进行参数估计

原文链接：http://tecdat.cn/?p=22828 

原文出处：拓端数据部落公众号

主要优化方法的快速概述

我们介绍主要的优化方法。我们考虑以下问题 .

无导数优化方法

Nelder-Mead方法是最著名的无导数方法之一，它只使用f的值来搜索最小值。过程：

1. 设置初始点x1,...,xn+1
2. 对点进行排序，使得f(x1)≤f(x2)≤⋯≤f(xn+1)。
3. 计算xo作为x1,...,xn的中心点。
4. 反射
   • 计算反射点xr=xo+α（xo-xn+1）。
   • 如果f(x1)≤f(xr)<f(xn)，那么用xr替换xn+1，转到步骤2。
   • 否则转到第5步。
5. 扩展:
   • 如果f(xr)<f(x1)，那么计算扩展点xe=xo+γ(xo−xn+1).
   • 如果f(xe)<f(xr)，那么用xe替换xn+1，转到步骤2。
   • 否则用xr替换xn+1，转到第2步。
   • 否则转到第6步。
6. 收缩:
   • 计算收缩点xc=xo+β（xo-xn+1）.
   • 如果f(xc)<f(xn+1)，那么用xc替换xn+1，进入第2步。
   • 否则转到第7步.
7. 减少:
   • 对于i=2,...,n+1，计算xi=x1+σ（xi-x1）.

Nelder-Mead方法在optim中可用。默认情况下，在optim中，α=1，β=1/2，γ=2，σ=1/2。

Hessian-free 优化方法

对于光滑的非线性函数，一般采用以下方法：局部方法结合直线搜索工作的方案xk+1=xk+tkdk，其中局部方法将指定方向dk，直线搜索将指定步长tk∈R。

基准

为了简化优化方法的基准，我们创建一个函数，用于计算所有优化方法的理想估计方法。

benchfit <- function(data, distr, ...) 

β分布的数值说明

β分布的对数似然函数及其梯度

理论值

β分布的密度由以下公式给出

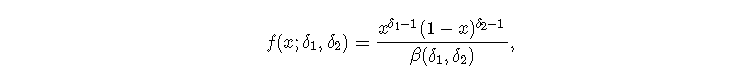
其中β表示β函数。我们记得β(a,b)=Γ(a)Γ(b)/Γ(a+b)。在这里，一组观测值（x1,...,xn）的对数似然性为

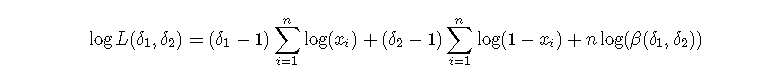
与a和b有关的梯度为

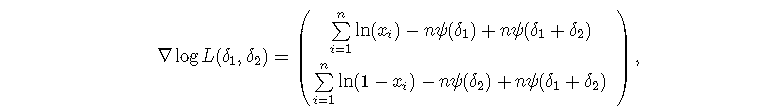
R实现

我们最小化了对数似然的相反数：实现了梯度的相反数。对数似然和它的梯度都不被输出。

1.  
   function(par)
2.  
   loglikelihood(par, fix.arg ,...)

 样本的随机生成 

1.  
   #(1) beta分布
2.  
   n <- 200
3.  
   x <- rbeta(n, 3, 3/4)
4.  
   lnl(c(3, 4), x) #检验

hist(x, prob=TRUE)

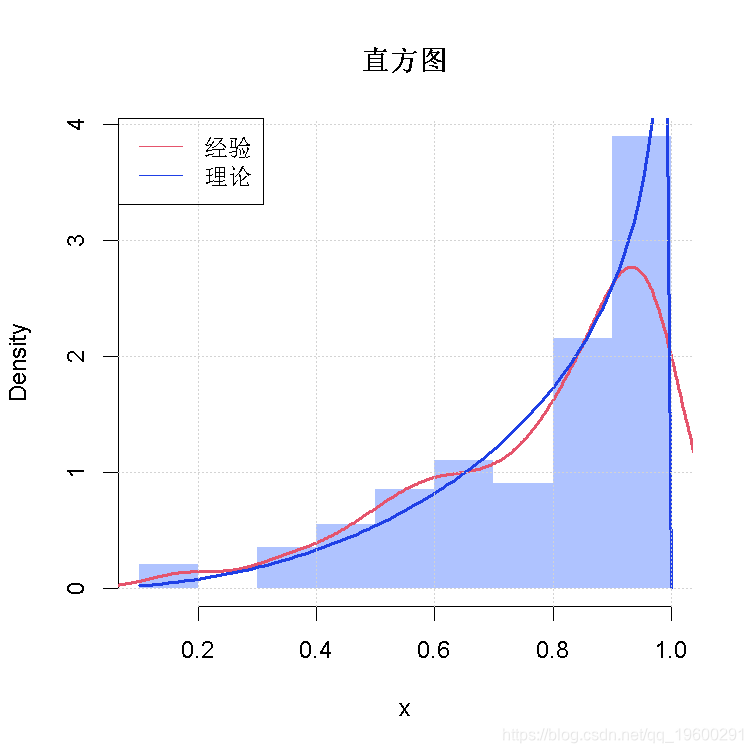
拟合Beta分布

定义控制参数。

list(REPORT=1, maxit=1000)

用默认的优化函数调用，对于不同的优化方法，有梯度和无梯度。

fit(x, "beta", "mle", lower=0,...)

 

在约束优化的情况下，我们通过使用对数障碍允许线性不平等约束。

使用形状参数δ1和δ2的exp/log变换，来确保形状参数严格为正。

1.  
    
2.  
   #取起始值的对数
3.  
   lapply(default(x, "beta"), log)
4.  
   #为新的参数化重新定义梯度
5.  
   exp <- function(par,...) beta(exp(par), obs) * exp(par)
6.  
   fit(x, distr="beta2", method="mle")

 

1.  
   #返回到原始参数化
2.  
   expopt <- exp(expopt)

然后，我们提取拟合参数的值、相应的对数似然值和要最小化的函数的计数及其梯度（无论是理论上的梯度还是数值上的近似值）。

数值调查的结果

结果显示在以下表格中。1）没有指定梯度的原始参数（-B代表有界版本），（2）具有（真实）梯度的原始参数（-B代表有界版本，-G代表梯度），（3）没有指定梯度的对数转换参数，（4）具有（真实）梯度的对数转换参数（-G代表梯度）。

 

 

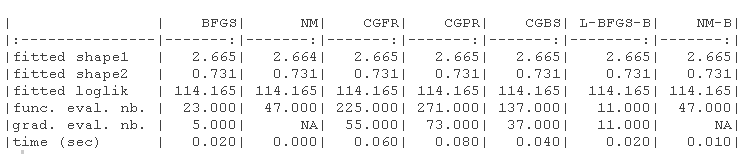
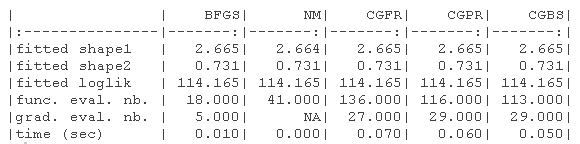
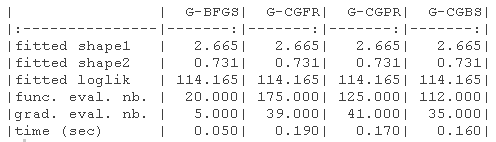
 我们绘制了真实值（绿色）和拟合参数（红色）周围的对数似然曲面图。

1.  
   llsurface(min.arg=c(0.1, 0.1), max.arg=c(7, 3),
2.  
   plot.arg=c("shape1", "shape2"), nlev=25,
3.  
   plot.np=50, data=x, distr="beta", back.col = FALSE)
4.  
   points(unconstropt[1,"BFGS"], unconstropt[2,"BFGS"], pch="+", col="red")
5.  
   points(3, 3/4, pch="x", col="green")

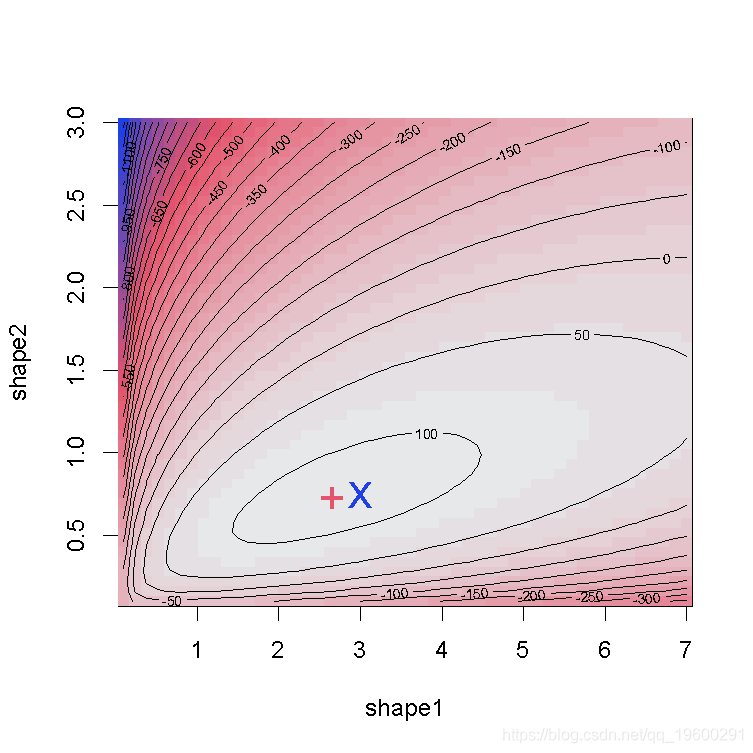
我们可以用bootdist函数来模拟bootstrap 复制的情况。

boot(fit(x, "beta", method="mle", optim.method="BFGS"))

1.  
   plot(b1)
2.  
   abline(v=3, h=3/4, col="red", lwd=1.5)

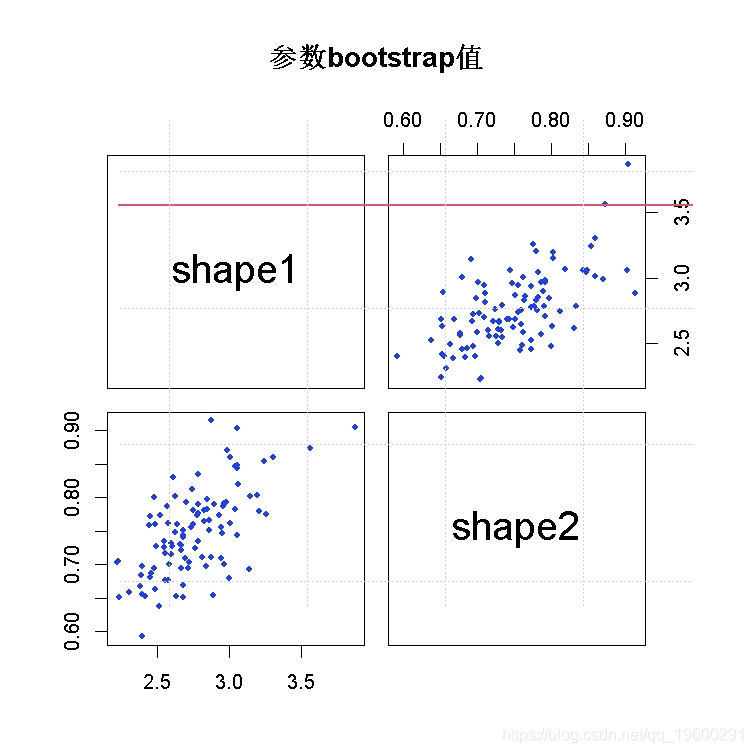
负二项分布的演示

负二项分布的对数似然函数及其梯度

理论值

负二项分布的p.m.f.由以下公式给出

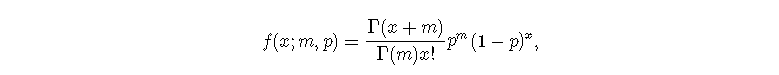
其中Γ表示β函数。存在另一种表示方法，即μ=m(1-p)/p或等价于p=m/(m+μ)。因此，一组观测值（x1,...,xn）的对数似然性是

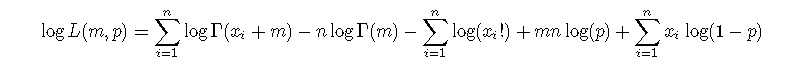
相对于m和p的梯度是

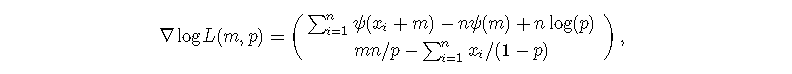
R实现

我们最小化对数似然性的相反数：实现梯度的相反数。

1.  
    
2.  
   m <- x[1]
3.  
   p <- x[2]
4.  
   c(sum(psigamma(obs+m)) - n*psigamma(m) + n*log(p),
5.  
   m*n/p - sum(obs)/(1-p))

样本的随机生成

1.  
   #(1) β分布
2.  
    
3.  
   trueval <- c("size"=10, "prob"=3/4, "mu"=10/3)
4.  
   x <- rnbinom(n, trueval["size"], trueval["prob"])
5.  
    
6.  
   hist(x, prob=TRUE, ylim=c(0, .3))

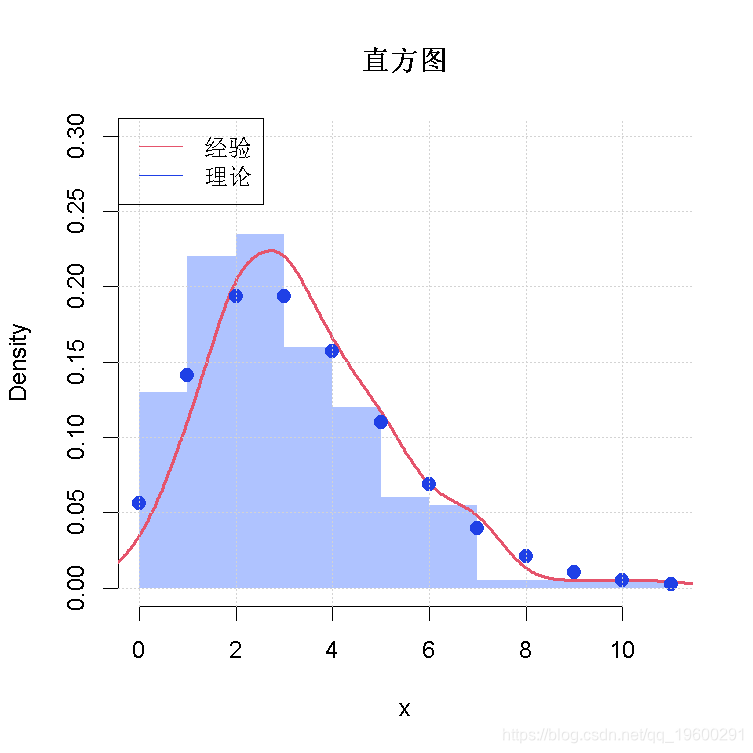
拟合负二项分布

定义控制参数并做基准。

1.  
   list(trace=0, REPORT=1, maxit=1000)
2.  
   fit(x, "nbinom", "mle", lower=0)

在约束优化的情况下，我们通过使用对数障碍允许线性不平等约束。

使用形状参数δ1和δ2的exp/log变换，来确保形状参数严格为正。

1.  
   #对起始值进行变换
2.  
   mu <- size / (size+mu)
3.  
   arg <- list(size=log(start), prob=log(start/(1-start)))
4.  
    
5.  
   #为新的参数化重新定义梯度
6.  
   function(x)
7.  
   c(exp(x[1]), plogis(x[2]))
8.  
    
9.  
   fit(x, distr="nbinom2", method="mle")

1.  
   #返回到原始参数化
2.  
   expo <- apply(expo, 2, Trans)

然后，我们提取拟合参数的值、相应的对数似然值和要最小化的函数的计数及其梯度（无论是理论上的梯度还是数值上的近似值）。

数值调查的结果

结果显示在以下表格中。1）没有指定梯度的原始参数（-B代表有界版本），（2）具有（真实）梯度的原始参数（-B代表有界版本，-G代表梯度），（3）没有指定梯度的对数转换参数，（4）具有（真实）梯度的对数转换参数（-G代表梯度）。

 

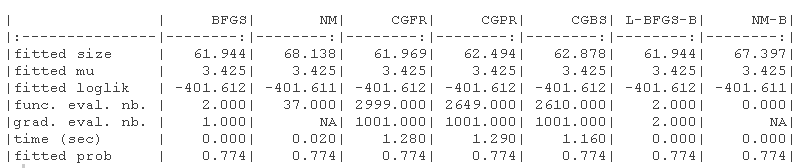
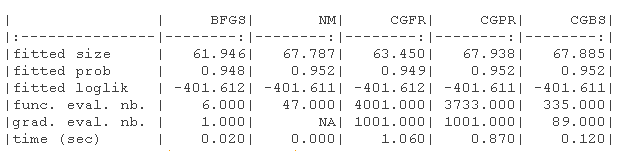
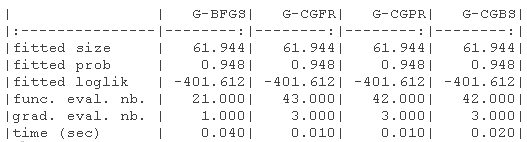
 我们绘制了真实值（绿色）和拟合参数（红色）周围的对数似然曲面图。

1.  
   surface(min.arg=c(5, 0.3), max.arg=c(15, 1),
2.  
   )
3.  
   points(trueval , pch="x")

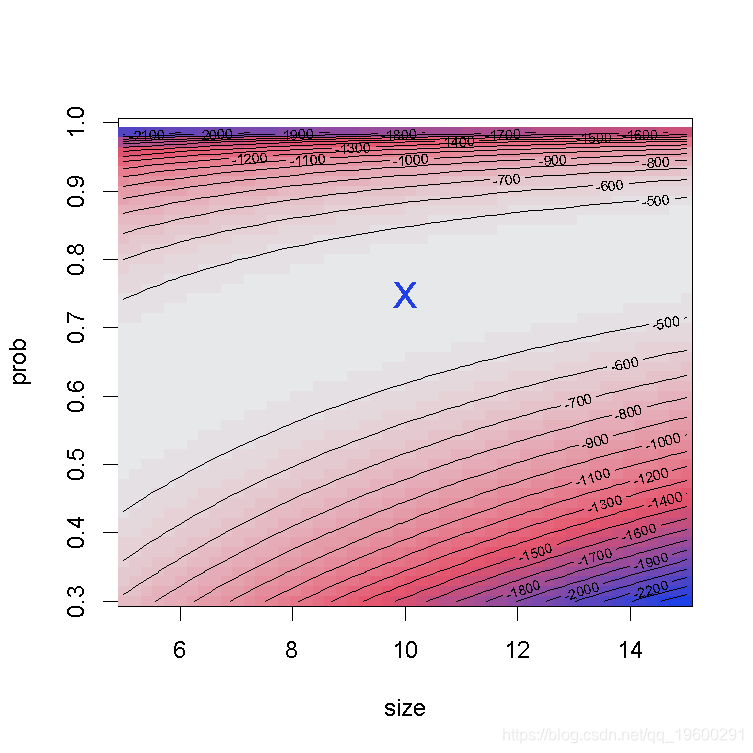
我们可以用bootdist函数来模拟bootstrap 复制的情况。

boot(fit(x, "nbinom", method="mle")

 

1.  
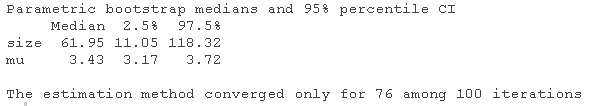
   plot(b1)
2.  
   abline(v=trueval)

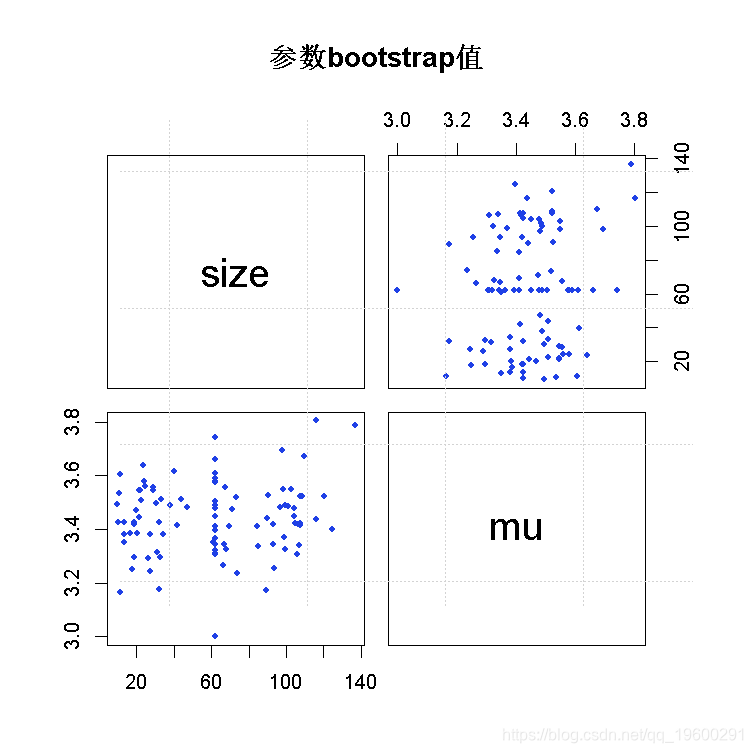
结论

基于前面的两个例子，我们观察到所有的方法都收敛到了同一个点。

然而，不同方法的函数评价（和梯度评价）的结果是非常不同的。此外，指定对数似然性的真实梯度对拟合过程没有任何帮助，通常会减慢收敛速度。一般来说，最好的方法是标准BFGS方法或对参数进行指数变换的BFGS方法。由于指数函数是可微的，所以渐进特性仍被保留（通过Delta方法），但对于有限样本来说，这可能会产生一个小的偏差。

---

最受欢迎的见解

1.Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV，Stochastic Volatility） 模型

2.基于R语言的疾病制图中自适应核密度估计的阈值选择方法

3.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

4.R语言回归中的hosmer-lemeshow拟合优度检验

5.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型估计

6.R语言区间数据回归分析

7.R语言WALD检验 VS 似然比检验

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标