拓端数据tecdat|Python用时变马尔可夫区制转换（Markov regime switching）自回归模型分析经济时间序列

原文链接：http://tecdat.cn/?p=22617

原文出处：拓端数据部落公众号

本文提供了一个在统计模型中使用马可夫转换模型模型的例子，来复现Kim和Nelson（1999）中提出的一些结果。它应用了Hamilton（1989）的滤波器和Kim（1994）的平滑器。

1.  
    
2.  
   %matplotlib inline
3.  
    
4.  
   import numpy as np
5.  
   import pandas as pd
6.  
   import statsmodels.api as sm
7.  
    
8.  
   from pandas_datareader.data import DataReader
9.  
   from datetime import datetime
10.  
    DataReader(start=datetime(1947, 1, 1), end=datetime(2013, 4, 1))

Hamilton (1989) 马尔可夫转换模型（Markov -switching model）

这是对Hamilton(1989)介绍马可夫转换模型（Markov -switching model）的开创性论文的复现。该模型是一个4阶的自回归模型，其中过程的平均值在两个区制之间切换。可以这样写。

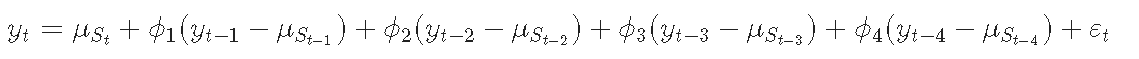
每个时期，区制都根据以下的转移概率矩阵进行转换。

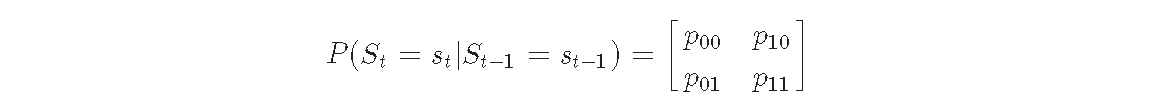
其中 pij是从区制 i 转移到区制 j 的概率。

该模型类别是时间序列部分中的MarkovAutoregression。为了创建这个模型，我们必须指定k_regimes=2的区制数量，以及order=4的自回归阶数。默认模型还包括转换自回归系数，所以在这里我们还需要指定switch_ar=False。

创建后，模型通过极大似然估计进行拟合。使用期望最大化（EM）算法的若干步骤找到好的起始参数，并应用准牛顿（BFGS）算法来快速找到最大值。

1.  
   [2]:
2.  
   #获取数据
3.  
   hamilton= pd.read('gndata').iloc[1:]
4.  
    
5.  
    
6.  
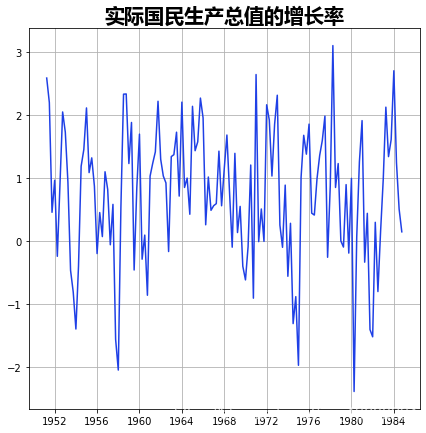
   # 绘制数据
7.  
   hamilton.plot()
8.  
    
9.  
   # 拟合模型
10.  
    Markovreg(hamilton)

summary()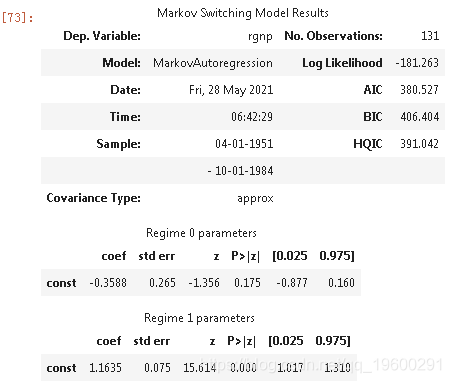

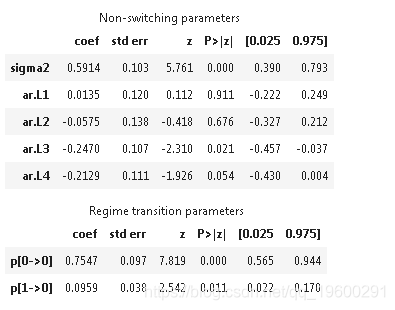
我们绘制了经过过滤和平滑处理的衰退概率。滤波指的是基于截至并包括时间tt（但不包括时间t+1,...,Tt+1,...,T）的数据对时间t的概率估计。平滑化是指使用样本中的所有数据对时间t的概率进行估计。

1.  
   fig, axes = plt.subplots(2, figsize=(7,7))
2.  
   ax = axes[0]
3.  
   ax.plot(margl_prob[0])
4.  
    
5.  
    
6.  
   ax = axes[1]
7.  
   ax.plot(smoomarginal_pro[0])
8.  
    

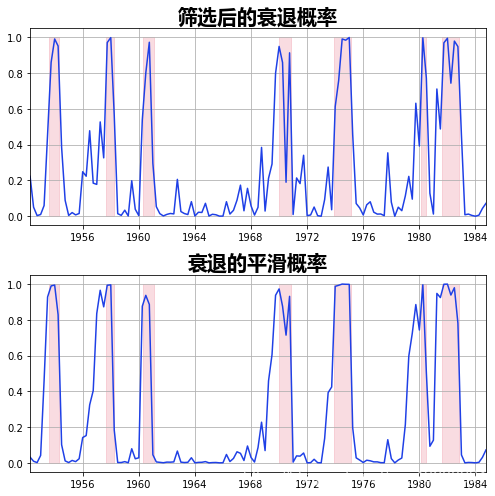
根据估计的转移矩阵，我们可以计算出衰退与扩张的预期持续时间。

print(expected_du)

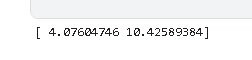
在这种情况下，预计经济衰退将持续约一年（4个季度），扩张约两年半。
 

Kim, Nelson, and Startz (1998) 三状态方差转换模型。
 

这个模型展示了带有区制异方差（方差转换）和无平均效应的估计。

模型是:

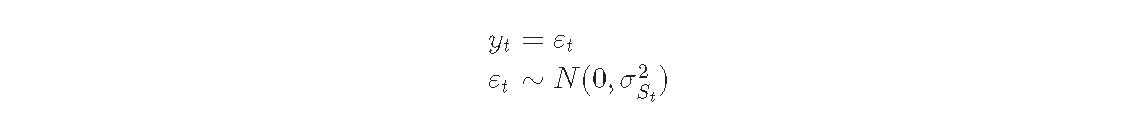
由于没有自回归成分，这个模型可以用MarkovRegression类来拟合。由于没有平均效应，我们指定趋势='nc'。假设转换方差有三个区制，所以我们指定k_regimes=3和switching_variance=True（默认情况下，方差被假定为在不同区制下是相同的）。

1.  
    
2.  
   raw = pd.read_table(ew ,engine='python')
3.  
    
4.  
   # 绘制数据集
5.  
   plot( figsize=(12, 3))
6.  
    

res_kns.summary()

 

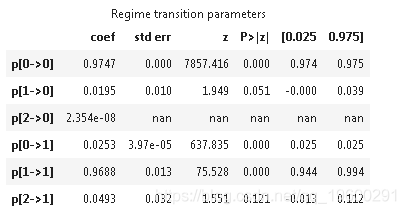
下面我们绘制了处于每个区制中的概率；只有在少数时期，才有可能出现高方差区制。

1.  
   fig, axes = plt.subplots(3, figsize=(10,7))
2.  
    
3.  
    
4.  
   ax.plot(smoothed_proba[0])
5.  
   ax.plot(smoothed_proba[2])
6.  
   ax.plot(smoothed_proba[3])

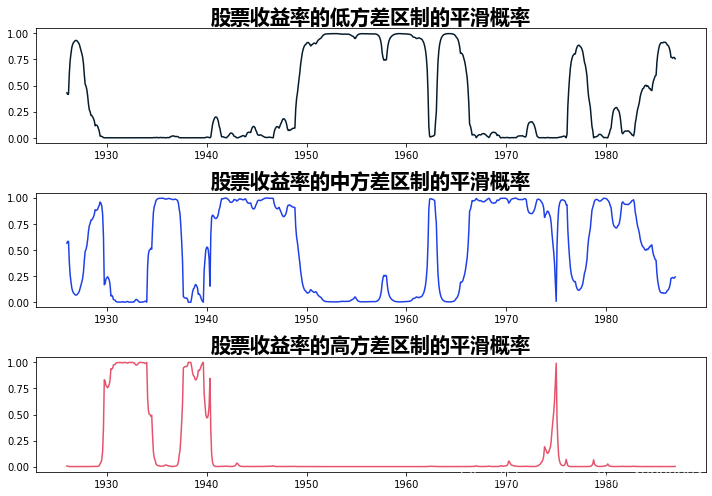
Filardo (1994) 时变的转移概率

这个模型展示了用时变的转移概率进行估计。

在上述模型中，我们假设转移概率在不同时期是不变的。在这里，我们允许概率随着经济状况的变化而变化。否则，该模型就是Hamilton（1989）的马尔可夫自回归。
每个时期，区制现在都根据以下的时变转移概率矩阵进行转移。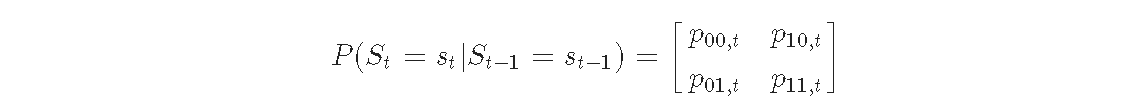

其中 pij,tipij,t 是在 t 期间从区制 i 转移到区制 j 的概率，并定义为。

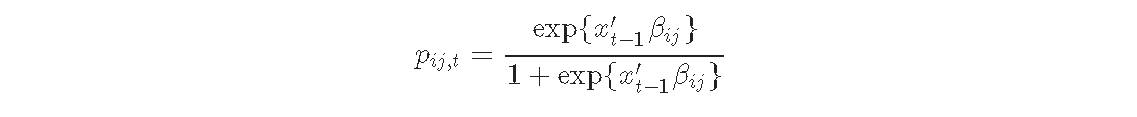
与其将转移概率作为最大似然法的一部分进行估计，不如估计回归系数βij。这些系数将转移概率与预先确定的或外生的变量xt-1向量联系起来。

[9]:

1.  
    
2.  
    
3.  
    
4.  
   # 用标准差进行标准化
5.  
    
6.  
   data['p']['1960-01-01':].std() / data['dlip'][:'1959-12-01'].std()
7.  
    
8.  
    
9.  
   # 绘制数据
10.  
    data['dlip'].plot( )
11.  
     
12.  
    data['dmdlleading'].plot( figsize=(13,3));

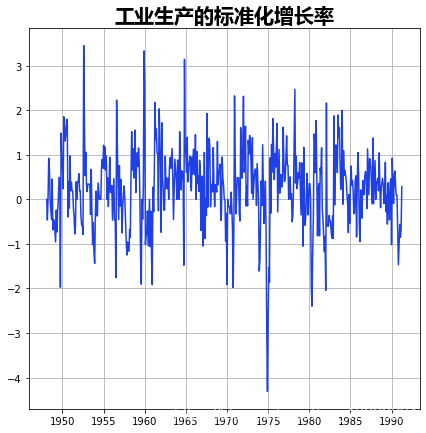
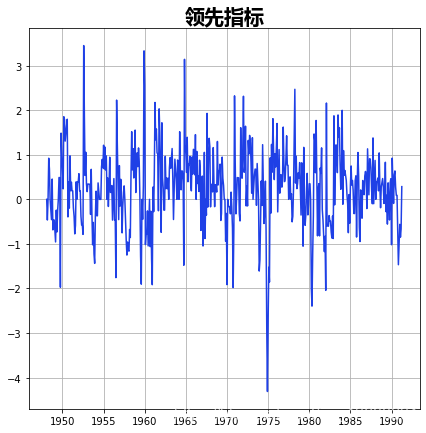
时变的转移概率是由exog_tvtp参数指定的。
 

这里我们展示了模型拟合的另一个特点--使用随机搜索的MLE起始参数。因为马尔科夫转换模型的特征往往是似然函数的许多局部最大值，执行初始优化步骤有助于找到最佳参数。
 

下面，我们规定对起始参数向量的20个随机扰动进行检查，并将最好的一个作为实际的起始参数。由于搜索的随机性，我们事先设置了随机数种子，以便结果复制。

1.  
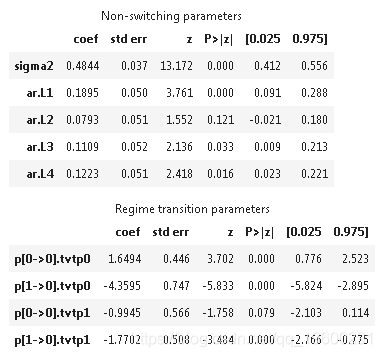
   markovreg(data, k=2, order=4)
2.  
    
3.  
   fit(search=20)
4.  
   summary()

 

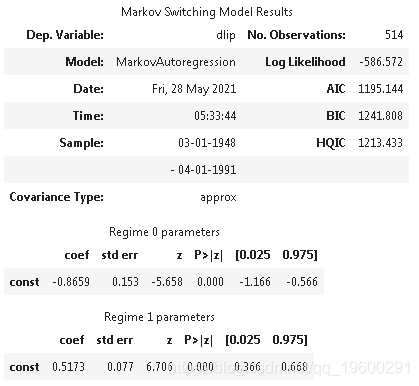
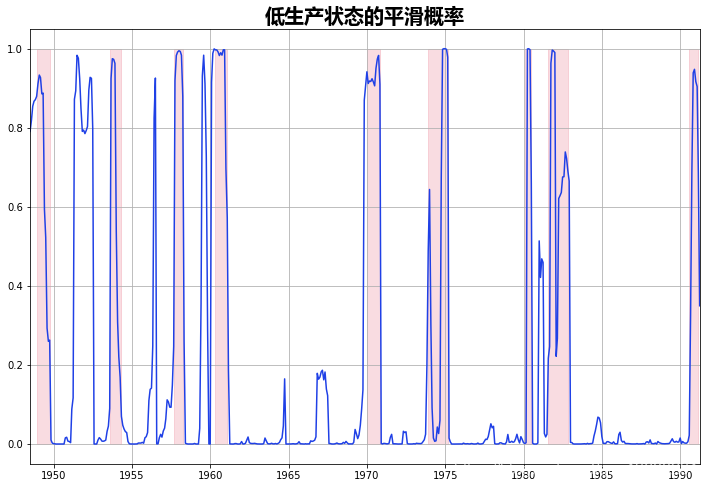
下面我们绘制了经济运行在低生产状态下的平滑概率，并再次将NBER的衰退情况纳入其中进行比较。

1.  
    
2.  
   ax.plot(smoo_marg_prob[0])

利用时间变化的转移概率，我们可以看到低生产状态的预期持续时间如何随时间变化。
 

exp_dura[0].plot( figsize=(12,3));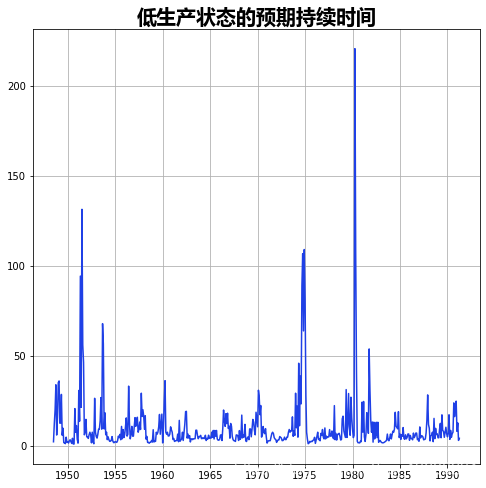

在经济衰退期间，低生产状态的预期持续时间要比经济扩张时高得多。

---

最受欢迎的见解

1.用R语言模拟混合制排队随机服务排队系统

2.R语言中使用排队论预测等待时间

3.R语言中实现马尔可夫链蒙特卡罗MCMC模型

4.R语言中的马尔科夫机制转换(Markov regime switching)模型

5.matlab贝叶斯隐马尔可夫hmm模型

6.用R语言模拟混合制排队随机服务排队系统

7.Python基于粒子群优化的投资组合优化

8.R语言马尔可夫转换模型研究交通伤亡人数事故预测

9.用机器学习识别不断变化的股市状况——隐马尔可夫模型的应用