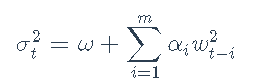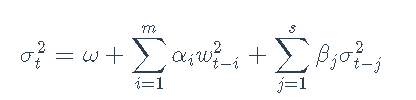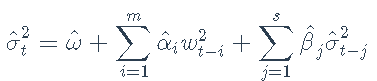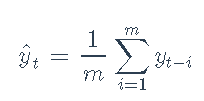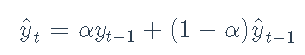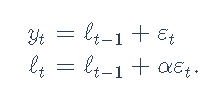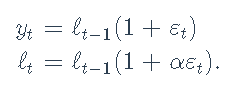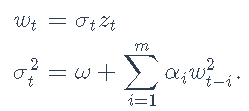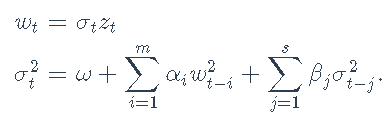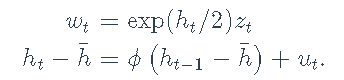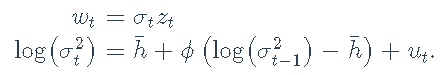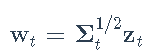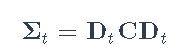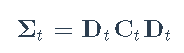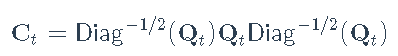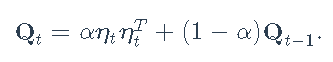拓端数据tecdat|R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模

拓端数据tecdat|R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
原文链接：http://tecdat.cn/?p=20015

本文将说明单变量和多变量金融时间序列的不同模型，特别是条件均值和条件协方差矩阵、波动率的模型。

均值模型

本节探讨条件均值模型。

iid模型

我们从简单的iid模型开始。iid模型假定对数收益率xt为N维高斯时间序列：

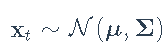
均值和协方差矩阵的样本估计量分别是样本均值

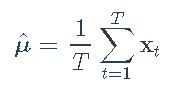
和样本协方差矩阵

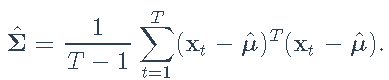
我们从生成数据开始，熟悉该过程并确保估计过程给出正确的结果（即完整性检查）。然后使用真实的市场数据并拟合不同的模型。

让我们生成合成iid数据并估算均值和协方差矩阵：
1. # 生成综合收益数据
2. X <- rmvnorm(n = T, mean = mu, sigma = Sigma)
3. # 样本估计（样本均值和样本协方差矩阵）
4. mu_sm <- colMeans(X)
5. Sigma_scm <- cov(X)
7. # 误差
8. norm(mu_sm - mu, "2")
9. #> [1] 2.44
10. norm(Sigma_scm - Sigma, "F")
11. #> [1] 70.79
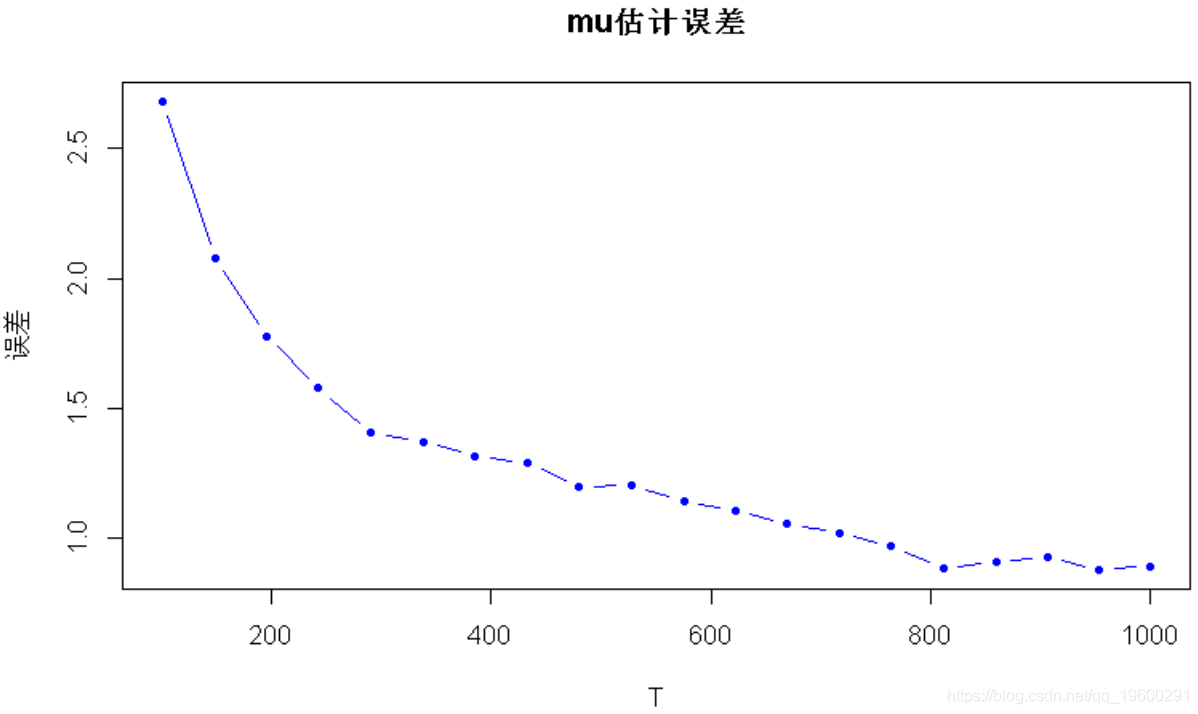
现在，让我们针对不同数量的观测值T再做一次：
1. # 首先生成所有数据
3. X <- rmvnorm(n = T_max, mean = mu, sigma = Sigma)
5. # 现在遍历样本的子集
7. for (T_ in T_sweep) {
9. # 样本估算
10. mu_sm <- colMeans(X_)
11. Sigma_scm <- cov(X_)
12. # 计算误差
13. error_mu_vs_T <- c(error_mu_vs_T, norm(mu_sm - mu, "2"))
14. error_Sigma_vs_T <- c(error_Sigma_vs_T, norm(Sigma_scm - Sigma, "F"))
16. # 绘图
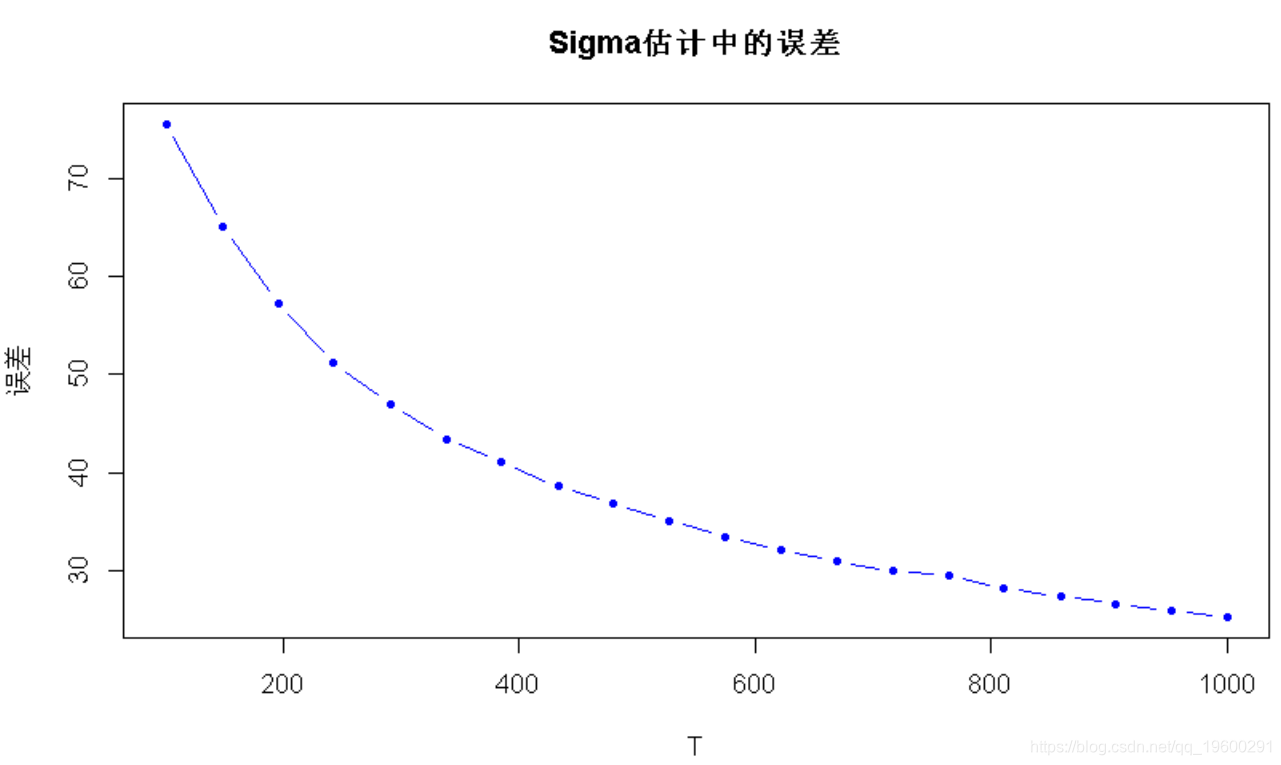
17. plot(T_sweep, error_mu_vs_T,
18. main = "mu估计误差",
1. plot(T_sweep, error_Sigma_vs_T
2. main = "Sigma估计中的误差", ylab = "误差"
单变量ARMA模型

对数收益率xt上的ARMA（p，q）模型是

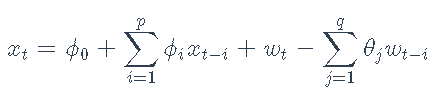
其中wt是均值为零且方差为σ2的白噪声序列。模型的参数是系数ϕi，θi和噪声方差σ2。

请注意，ARIMA（p，d，q）模型是时间差分为d阶的ARMA（p，q）模型。因此，如果我们用xt代替对数价格，那么先前的对数收益模型实际上就是ARIMA（p，1，q）模型，因为一旦对数价格差分，我们就获得对数收益。

rugarch生成数据

我们将使用rugarch包生成单变量ARMA数据，估计参数并进行预测。

首先，我们需要定义模型：
2. #指定具有给定系数和参数的AR（1）模型
4. #>
5. #> *----------------------------------*
6. #> * ARFIMA Model Spec *
7. #> *----------------------------------*
8. #> Conditional Mean Dynamics
9. #> ------------------------------------
10. #> Mean Model : ARFIMA(1,0,0)
11. #> Include Mean : TRUE
12. #>
13. #> Conditional Distribution
14. #> ------------------------------------
15. #> Distribution : norm
16. #> Includes Skew : FALSE
17. #> Includes Shape : FALSE
18. #> Includes Lambda : FALSE
21. #> Level Fixed Include Estimate LB UB
22. #> mu 0.01 1 1 0 NA NA
23. #> ar1 -0.90 1 1 0 NA NA
24. #> ma 0.00 0 0 0 NA NA
25. #> arfima 0.00 0 0 0 NA NA
26. #> archm 0.00 0 0 0 NA NA
27. #> mxreg 0.00 0 0 0 NA NA
28. #> sigma 0.20 1 1 0 NA NA
29. #> alpha 0.00 0 0 0 NA NA
30. #> beta 0.00 0 0 0 NA NA
31. #> gamma 0.00 0 0 0 NA NA
32. #> eta1 0.00 0 0 0 NA NA
33. #> eta2 0.00 0 0 0 NA NA
34. #> delta 0.00 0 0 0 NA NA
35. #> lambda 0.00 0 0 0 NA NA
36. #> vxreg 0.00 0 0 0 NA NA
37. #> skew 0.00 0 0 0 NA NA
38. #> shape 0.00 0 0 0 NA NA
39. #> ghlambda 0.00 0 0 0 NA NA
40. #> xi 0.00 0 0 0 NA NA
42. fixed.pars
43. #> $mu
44. #> [1] 0.01
45. #>
46. #> $ar1
47. #> [1] -0.9
48. #>
49. #> $sigma
50. #> [1] 0.2
52. true_params
53. #> mu ar1 sigma
54. #> 0.01 -0.90 0.20
然后，我们可以生成时间序列：
2. # 模拟一条路径
4. apath(spec, n.sim = T)
7. # 转换为xts并绘图
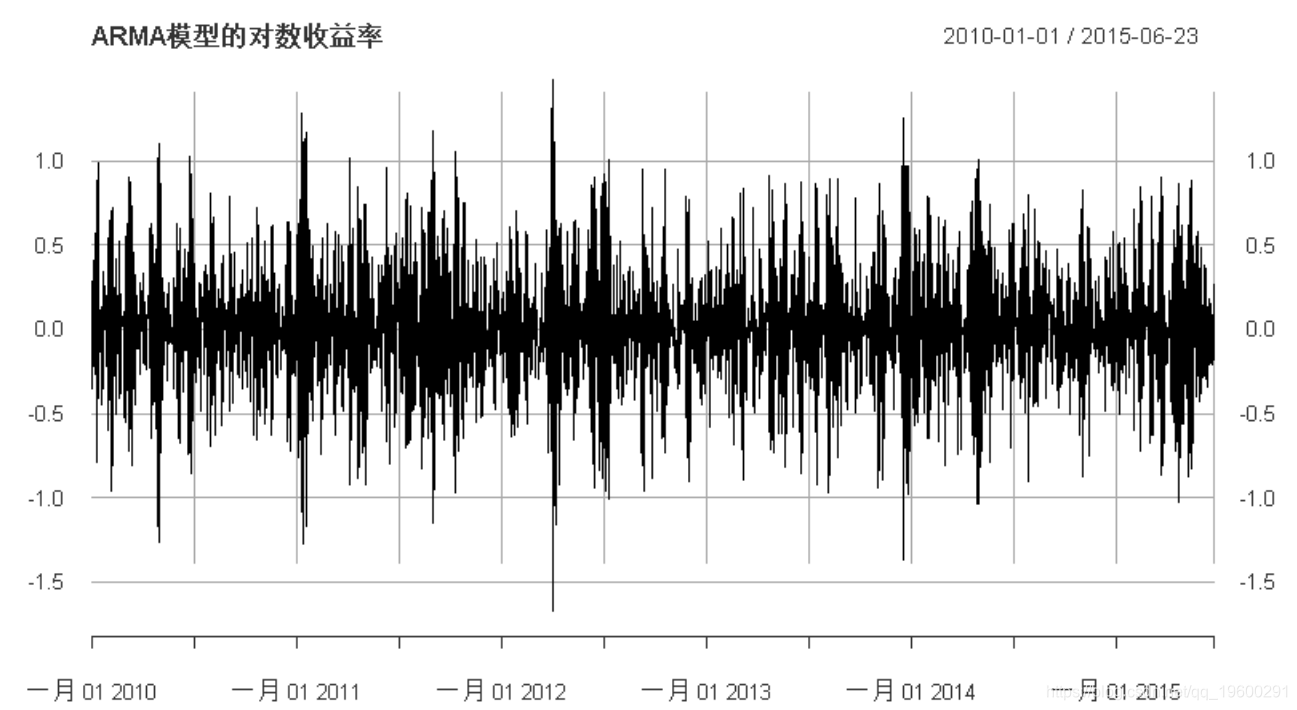
8. plot(synth_log_returns, main = "ARMA模型的对数收益率"
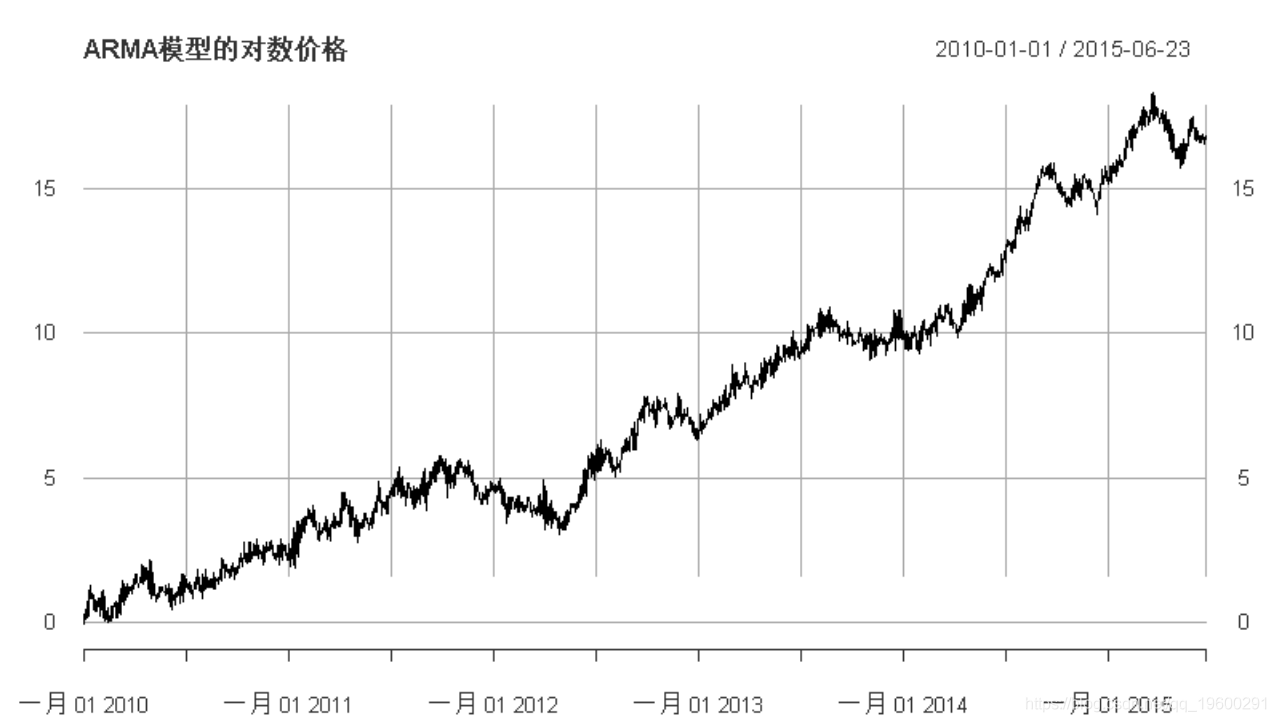
9. plot(synth_log_prices, main = "ARMA模型的对数价格"
ARMA模型

现在，我们可以估计参数（我们已经知道）：
1. # 指定AR（1）模型
2. arfimaspec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE))
4. # 估计模型
6. #> mu ar1 sigma
7. #> 0.0083 -0.8887 0.1987
9. #> mu ar1 sigma
10. #> 0.01 -0.90 0.20
我们还可以研究样本数量T对参数估计误差的影响：
1. # 循环
3. for (T_ in T_sweep) {
4. estim_coeffs_vs_T <- rbind(estim_coeffs_vs_T, coef(arma_fit))
5. error_coeffs_vs_T <- rbind(error_coeffs_vs_T, abs(coef(arma_fit) - true_params)/true_params)
8. # 绘图
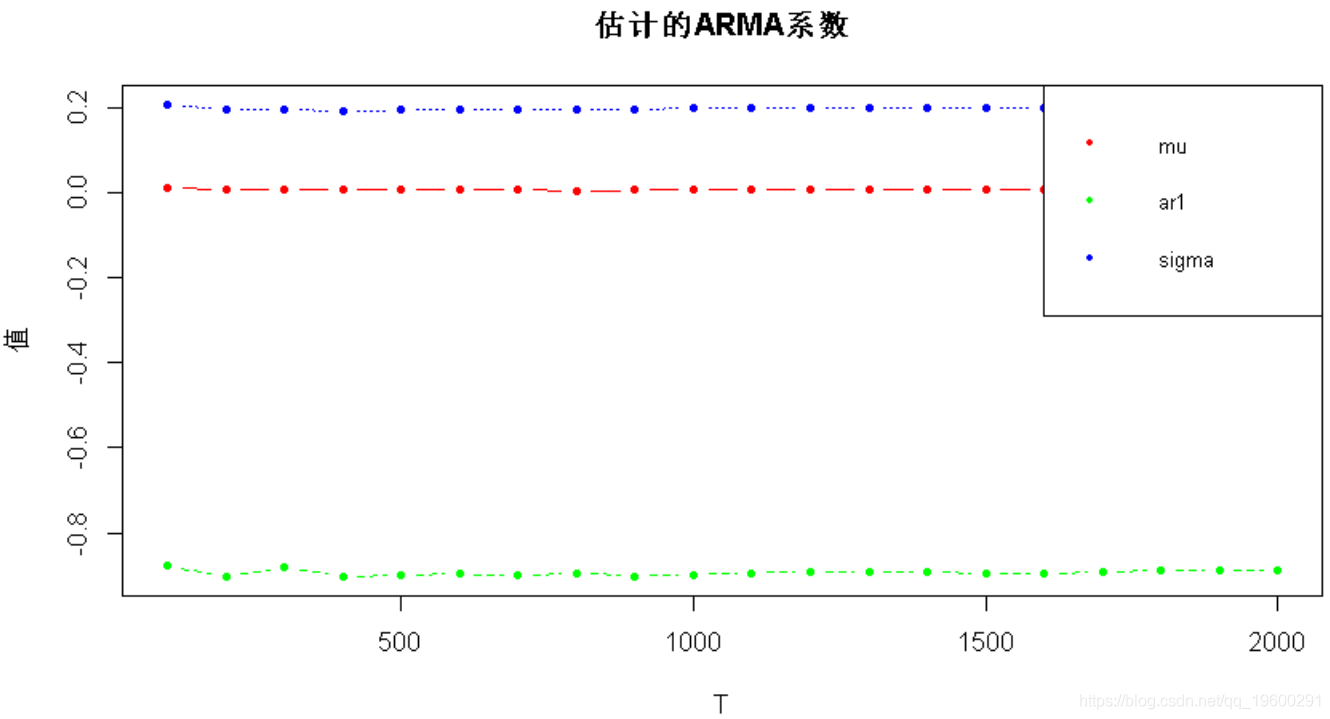
9. matplot(T_sweep, estim_coeffs_vs_T,
10. main = "估计的ARMA系数", xlab = "T", ylab = "值",
1. matplot(T_sweep, 100*error_coeffs_vs_T,
2. main = "估计ARMA系数的相对误差", xlab = "T", ylab = "误差 (%)",
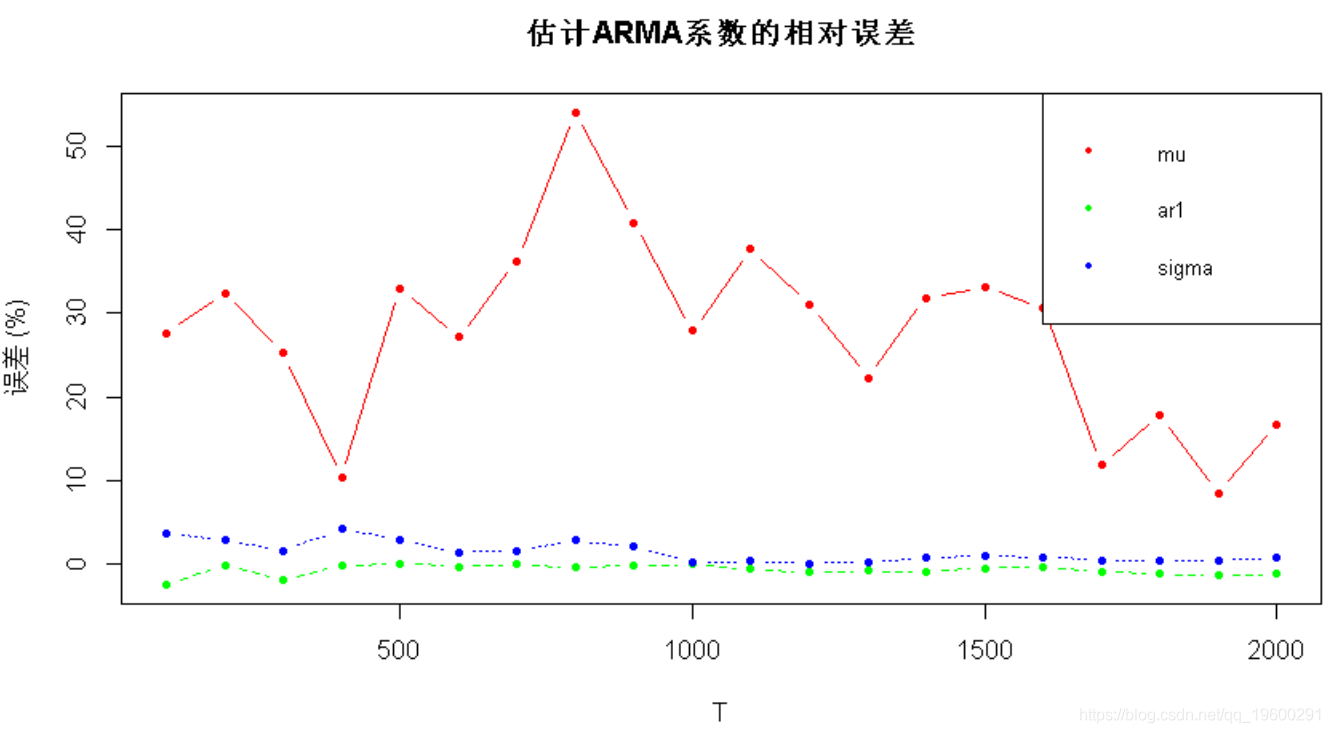
首先，真正的μ几乎为零，因此相对误差可能显得不稳定。在T = 800个样本之后，其他系数得到了很好的估计。

ARMA预测

为了进行健全性检查，我们现在将比较两个程序包 Forecast 和 rugarch的结果：
2. # 指定具有给定系数和参数的AR（1）模型
3. spec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE),
4. fixed.pars = list(mu = 0.005, ar1 = -0.9, sigma = 0.1))
6. # 生成长度为1000的序列
7. arfima(arma_fixed_spec, n.sim = 1000)@path$seriesSim
9. # 使用 rugarch包指定和拟合模型
10. spec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE))
12. # 使用包“ forecast”拟合模型
14. #> ARIMA(1,0,0) with non-zero mean
15. #>
16. #> Coefficients:
17. #> ar1 mean
18. #> -0.8982 0.0036
19. #> s.e. 0.0139 0.0017
20. #>
21. #> sigma^2 estimated as 0.01004: log likelihood=881.6
22. #> AIC=-1757.2 AICc=-1757.17 BIC=-1742.47
24. # 比较模型系数
26. #> ar1 intercept sigma
27. #> -0.898181148 0.003574781 0.100222964
29. #> mu ar1 sigma
30. #> 0.003605805 -0.898750138 0.100199956
确实，这两个软件包给出了相同的结果。

ARMA模型选择

在先前的实验中，我们假设我们知道ARMA模型的阶数，即p = 1和q = 0。实际上，阶数是未知的，因此必须尝试不同的阶数组合。阶数越高，拟合越好，但这将不可避免地导致过度拟合。已经开发出许多方法来惩罚复杂性的增加以避免过度拟合，例如AIC，BIC，SIC，HQIC等。
3. # 尝试不同的组合
5. # 查看排名
6. #> AR MA Mean ARFIMA BIC converged
7. #> 1 1 0 1 0 -0.38249098 1
8. #> 2 1 1 1 0 -0.37883157 1
9. #> 3 2 0 1 0 -0.37736340 1
10. #> 4 1 2 1 0 -0.37503980 1
11. #> 5 2 1 1 0 -0.37459177 1
12. #> 6 3 0 1 0 -0.37164609 1
13. #> 7 1 3 1 0 -0.37143480 1
14. #> 8 2 2 1 0 -0.37107841 1
15. #> 9 3 1 1 0 -0.36795491 1
16. #> 10 2 3 1 0 -0.36732669 1
17. #> 11 3 2 1 0 -0.36379209 1
18. #> 12 3 3 1 0 -0.36058264 1
19. #> 13 0 3 1 0 -0.11875575 1
20. #> 14 0 2 1 0 0.02957266 1
21. #> 15 0 1 1 0 0.39326050 1
22. #> 16 0 0 1 0 1.17294875 1
24. #选最好的
26. armaOrder
27. #> AR MA
28. #> 1 0
在这种情况下，由于观察次数T = 1000足够大，因此阶数被正确地检测到。相反，如果尝试使用T = 200，则检测到的阶数为p = 1，q = 3。

ARMA预测

一旦估计了ARMA模型参数ϕi ^ i和θ^j，就可以使用该模型预测未来的值。例如，根据过去的信息对xt的预测是

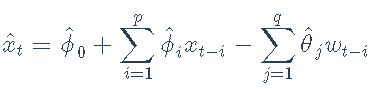
并且预测误差将为xt-x ^ t = wt（假设参数已被估计），其方差为σ2。软件包 rugarch 使对样本外数据的预测变得简单：
1. # 估计模型（不包括样本外）
3. coef(arma_fit)
4. #> mu ar1 sigma
5. #> 0.007212069 -0.898745183 0.200400119
7. # 整个样本外的预测对数收益
8. forecast_log_returns <- xts(arma_fore@forecast$seriesFor[1, ], dates_out_of_sample)
10. # 恢复对数价格
11. prev_log_price <- head(tail(synth_log_prices, out_of_sample+1), out_of_sample)
13. # 对数收益图
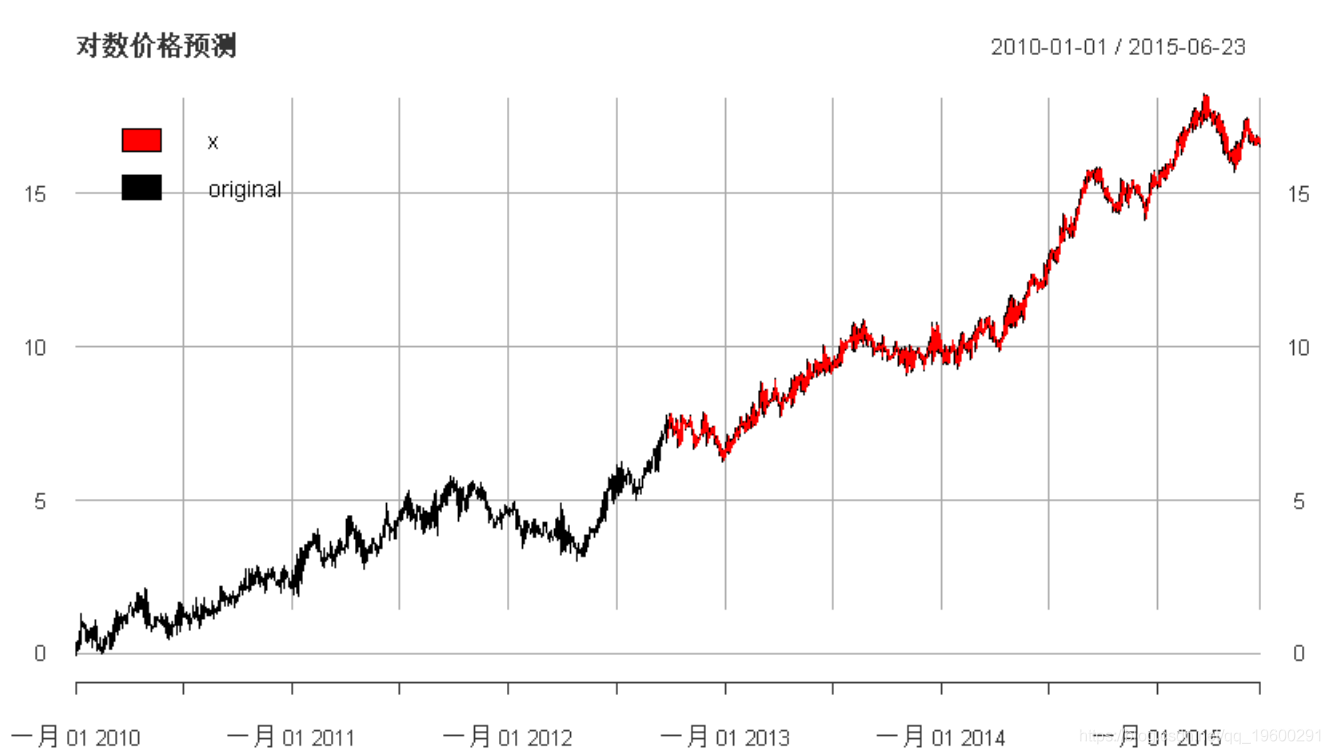
14. plot(cbind("fitted" = fitted(arma_fit),
16. # 对数价格图
17. plot(cbind("forecast" = forecast_log_prices,
19. main = "对数价格预测", legend.loc = "topleft")
多元VARMA模型

对数收益率xt上的VARMA（p，q）模型是

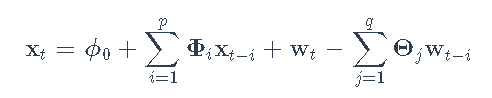
其中wt是具有零均值和协方差矩阵Σw的白噪声序列。该模型的参数是矢量/矩阵系数ϕ0，Φi，Θj和噪声协方差矩阵Σw。

比较

让我们首先加载S＆P500：
2. # 加载标普500数据
4. head(SP500_index_prices)
5. #> SP500
6. #> 2012-01-03 1277.06
7. #> 2012-01-04 1277.30
8. #> 2012-01-05 1281.06
9. #> 2012-01-06 1277.81
10. #> 2012-01-09 1280.70
11. #> 2012-01-10 1292.08
13. # 准备训练和测试数据
15. logreturns_trn <- logreturns[1:T_trn]
16. logreturns_tst <- logreturns[-c(1:T_trn)]
18. # 绘图
19. { plot(logreturns,
20. addEventLines(xts("训练"
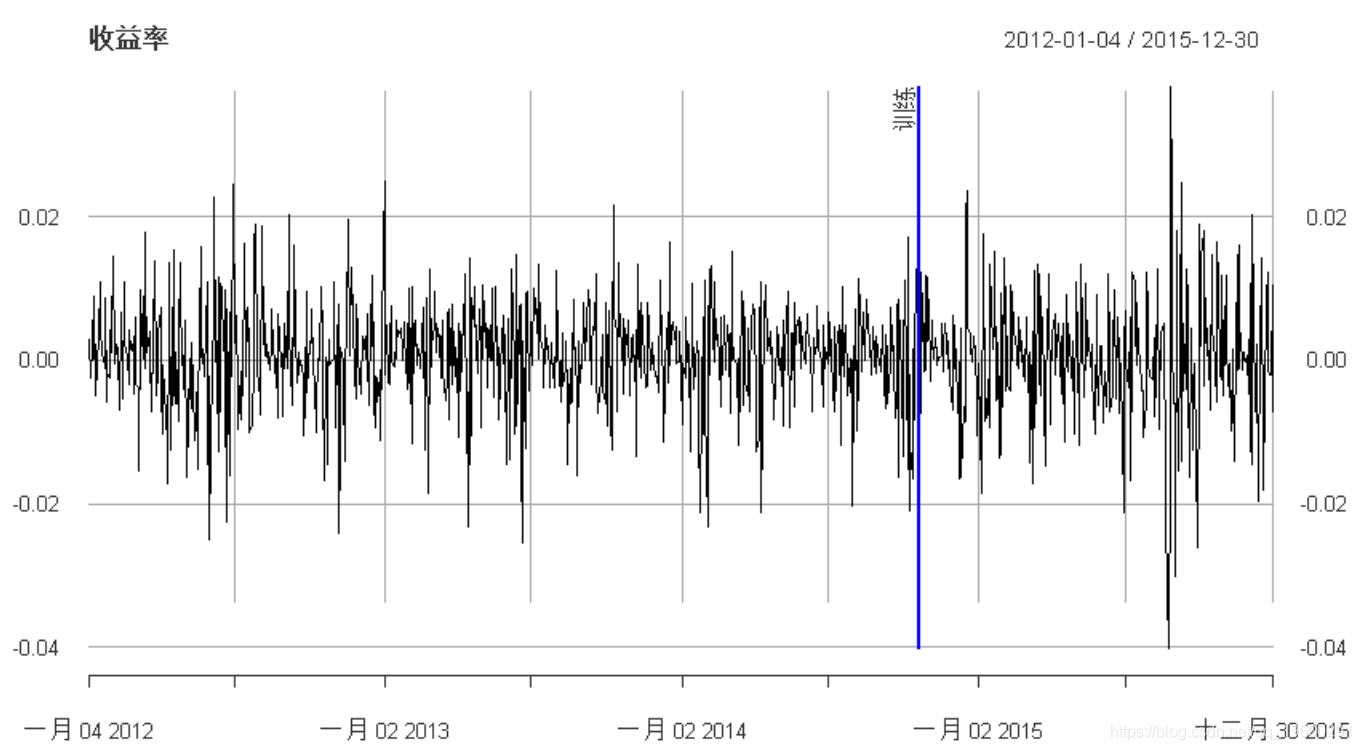
现在，我们使用训练数据（即，对于t = 1，…，Ttrnt = 1，…，Ttrn）来拟合不同的模型（请注意，通过指示排除了样本外数据 out.sample = T_tst）。特别是，我们将考虑iid模型，AR模型，ARMA模型以及一些ARCH和GARCH模型（稍后将对方差建模进行更详细的研究）。
2. # 拟合i.i.d.模型
4. coef(iid_fit)
5. #> mu sigma
6. #> 0.0005712982 0.0073516993
7. mean(logreturns_trn)
8. #> [1] 0.0005681388
9. sd(logreturns_trn)
10. #> [1] 0.007360208
12. # 拟合AR（1）模型
14. coef(ar_fit)
15. #> mu ar1 sigma
16. #> 0.0005678014 -0.0220185181 0.0073532716
18. # 拟合ARMA（2,2）模型
20. coef(arma_fit)
21. #> mu ar1 ar2 ma1 ma2 sigma
22. #> 0.0007223304 0.0268612636 0.9095552008 -0.0832923604 -0.9328475211 0.0072573570
24. # 拟合ARMA（1,1）+ ARCH（1）模型
26. coef(arch_fit)
27. #> mu ar1 ma1 omega alpha1
28. #> 6.321441e-04 8.720929e-02 -9.391019e-02 4.898885e-05 9.986975e-02
30. #拟合ARMA（0,0）+ARCH（10）模型
32. coef(long_arch_fit)
33. #> mu omega alpha1 alpha2 alpha3 alpha4 alpha5
34. #> 7.490786e-04 2.452099e-05 6.888561e-02 7.207551e-02 1.419938e-01 1.909541e-02 3.082806e-02
35. #> alpha6 alpha7 alpha8 alpha9 alpha10
36. #> 4.026539e-02 3.050040e-07 9.260183e-02 1.150128e-01 1.068426e-06
38. # 拟合ARMA（1,1）+GARCH（1,1）模型
40. coef(garch_fit)
41. #> mu ar1 ma1 omega alpha1 beta1
42. #> 6.660346e-04 9.664597e-01 -1.000000e+00 7.066506e-06 1.257786e-01 7.470725e-01
我们使用不同的模型来预测对数收益率：
1. # 准备预测样本外周期的对数收益
3. # i.i.d.模型预测
4. forecast(iid_fit, n.ahead = 1, n.roll = T_tst - 1)
5. dates_out_of_sample)
7. # AR（1）模型进行预测
8. forecast(ar_fit, n.ahead = 1, n.roll = T_tst - 1)
9. dates_out_of_sample)
11. # ARMA（2,2）模型进行预测
12. forecast(arma_fit, n.ahead = 1, n.roll = T_tst - 1)
13. dates_out_of_sample)
15. # 使用ARMA（1,1）+ ARCH（1）模型进行预测
16. forecast(arch_fit, n.ahead = 1, n.roll = T_tst - 1)
17. dates_out_of_sample)
19. # ARMA（0,0）+ARCH（10）模型预测
20. forecast(long_arch_fit, n.ahead = 1, n.roll = T_tst - 1)
21. dates_out_of_sample)
23. # ARMA（1,1）+GARCH（1,1）模型预测
24. forecast(garch_fit, n.ahead = 1, n.roll = T_tst - 1)
25. dates_out_of_sample)
我们可以计算不同模型的预测误差（样本内和样本外）：
2. print(error_var)
3. #> in-sample out-of-sample
4. #> iid 5.417266e-05 8.975710e-05
5. #> AR(1) 5.414645e-05 9.006139e-05
6. #> ARMA(2,2) 5.265204e-05 1.353213e-04
7. #> ARMA(1,1) + ARCH(1) 5.415836e-05 8.983266e-05
8. #> ARCH(10) 5.417266e-05 8.975710e-05
9. #> ARMA(1,1) + GARCH(1,1) 5.339071e-05 9.244012e-05
我们可以观察到，随着模型复杂度的增加，样本内误差趋于变小（由于拟合数据的自由度更高），尽管差异可以忽略不计。重要的实际上是样本外误差：我们可以看到，增加模型复杂度可能会得出较差的结果。就预测收益的误差而言，似乎最简单的iid模型已经足够了。

最后，让我们展示一些样本外误差的图表：
2. plot(error,
3. main = "不同模型收益预测的样本外误差",
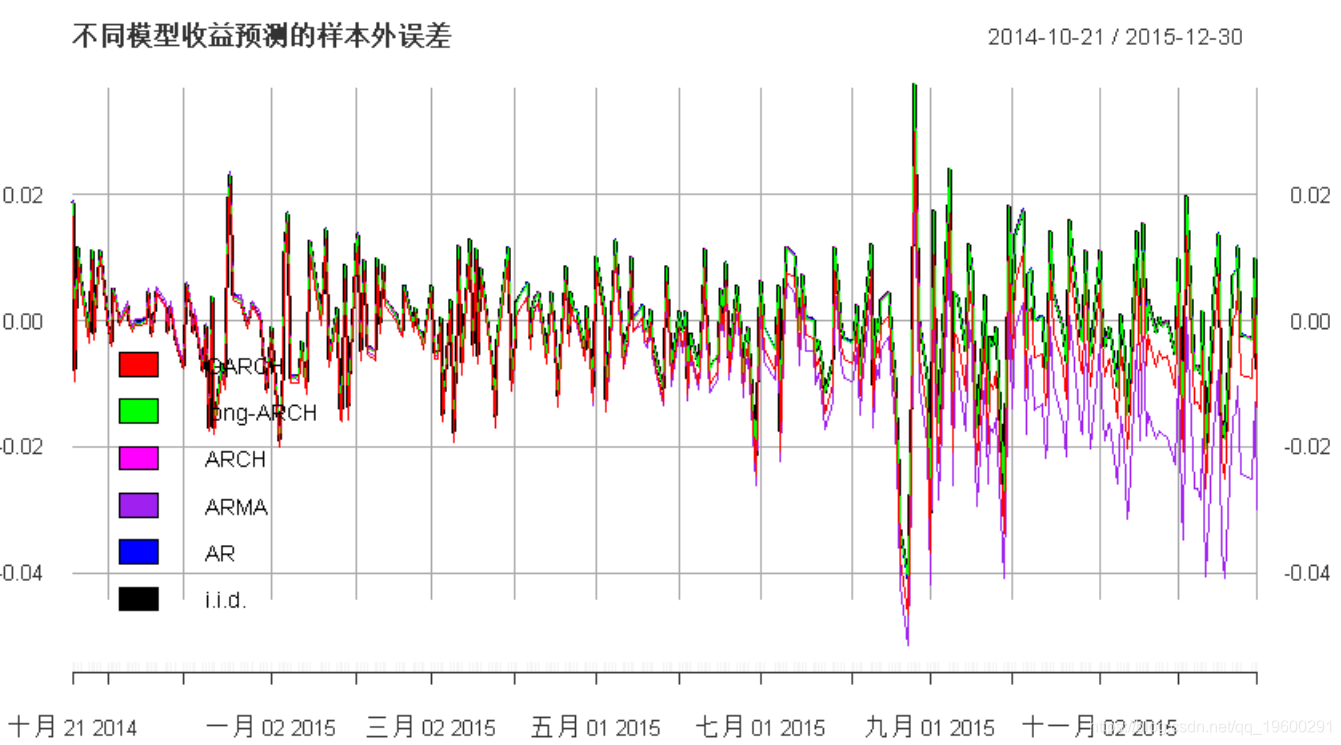
请注意，由于我们没有重新拟合模型，因此随着时间的发展，误差越大（对于ARCH建模尤其明显）。

滚动窗口比较

让我们首先通过一个简单的示例比较静态预测与滚动预测的概念：
1. #ARMA（2,2）模型
2. spec <- spec(mean.model = list(armaOrder = c(2,2), include.mean = TRUE))
4. # 静态拟合和预测
5. ar_static_fit <- fit(spec = spec, data = logreturns, out.sample = T_tst)
7. #滚动拟合和预测
8. modelroll <- aroll(spec = spec, data = logreturns, n.ahead = 1,
11. # 预测图
12. plot(cbind("static forecast" = ar_static_fore_logreturns,
13. main = "使用ARMA（2,2）模型进行预测", legend.loc = "topleft")
15. # 预测误差图
17. plot(error_logreturns, col = c("black", "red"), lwd = 2,
18. main = "ARMA（2,2）模型的预测误差", legend.loc = "topleft")
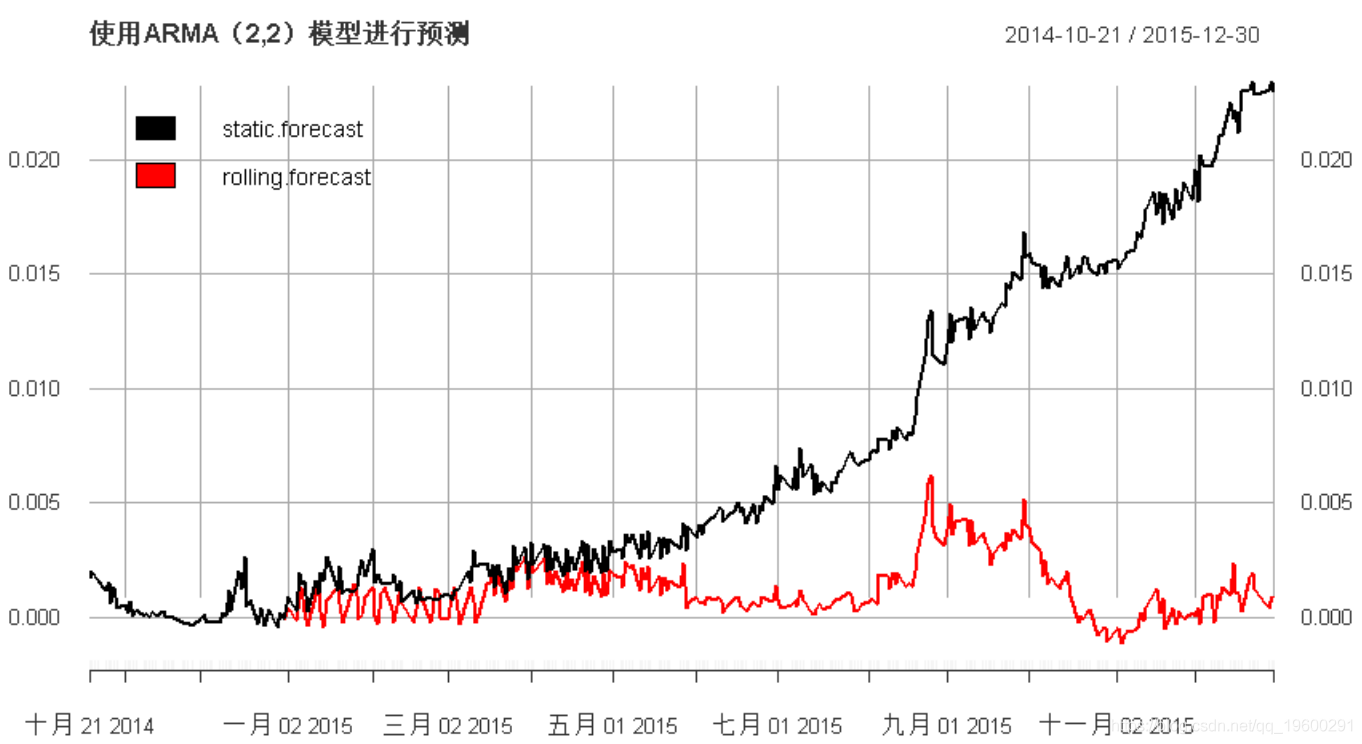
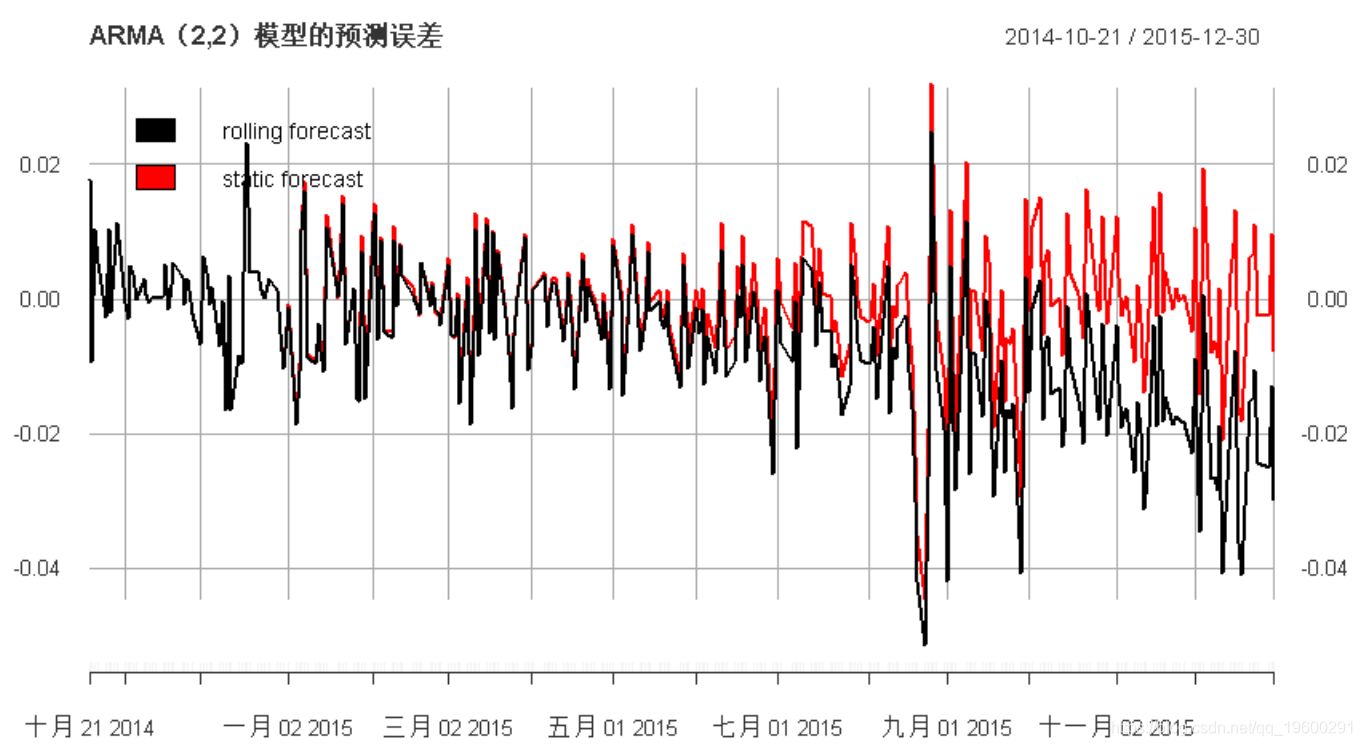
我们可以清楚地观察到滚动窗口过程对时间序列的影响。

现在，我们可以在滚动窗口的基础上重做所有模型的所有预测：
1. # 基于i.i.d.模型的滚动预测
2. roll(iid_spec, data = logreturns, n.ahead = 1, forecast.length = T_t
4. # AR（1）模型的滚动预测
5. roll(ar_spec, data = logreturns, n.ahead = 1, forecast.length = T_tst,
7. # ARMA（2,2）模型的滚动预测
8. roll(arma_spec, data = logreturns, n.ahead = 1, forecast.length = T_tst,
10. # ARMA（1,1）+ ARCH（1）模型的滚动预测
11. roll(arch_spec, data = logreturns, n.ahead = 1, forecast.length = T_tst,
12. refit.every = 50, refit.win
14. # ARMA（0,0）+ ARCH（10）模型的滚动预测
15. roll(long_arch_spec, data = logreturns, n.ahead = 1, forecast.length = T_tst,
16. refit.every = 50,
18. # ARMA（1,1）+ GARCH（1,1）模型的滚动预测
19. roll(garch_spec, data = logreturns, n.ahead = 1, forecast.length = T_tst,
20. refit.every = 50, refit.window
让我们看看滚动基准情况下的预测误差：
2. print(rolling_error_var)
3. #> in-sample out-of-sample
4. #> iid 5.417266e-05 8.974166e-05
5. #> AR(1) 5.414645e-05 9.038057e-05
6. #> ARMA(2,2) 5.265204e-05 8.924223e-05
7. #> ARMA(1,1) + ARCH(1) 5.415836e-05 8.991902e-05
8. #> ARCH(10) 5.417266e-05 8.976736e-05
9. #> ARMA(1,1) + GARCH(1,1) 5.339071e-05 8.895682e-05
和一些图表：
2. plot(error_logreturns,
3. main = "不同模型的滚动预测误差", legend.loc = "topleft"
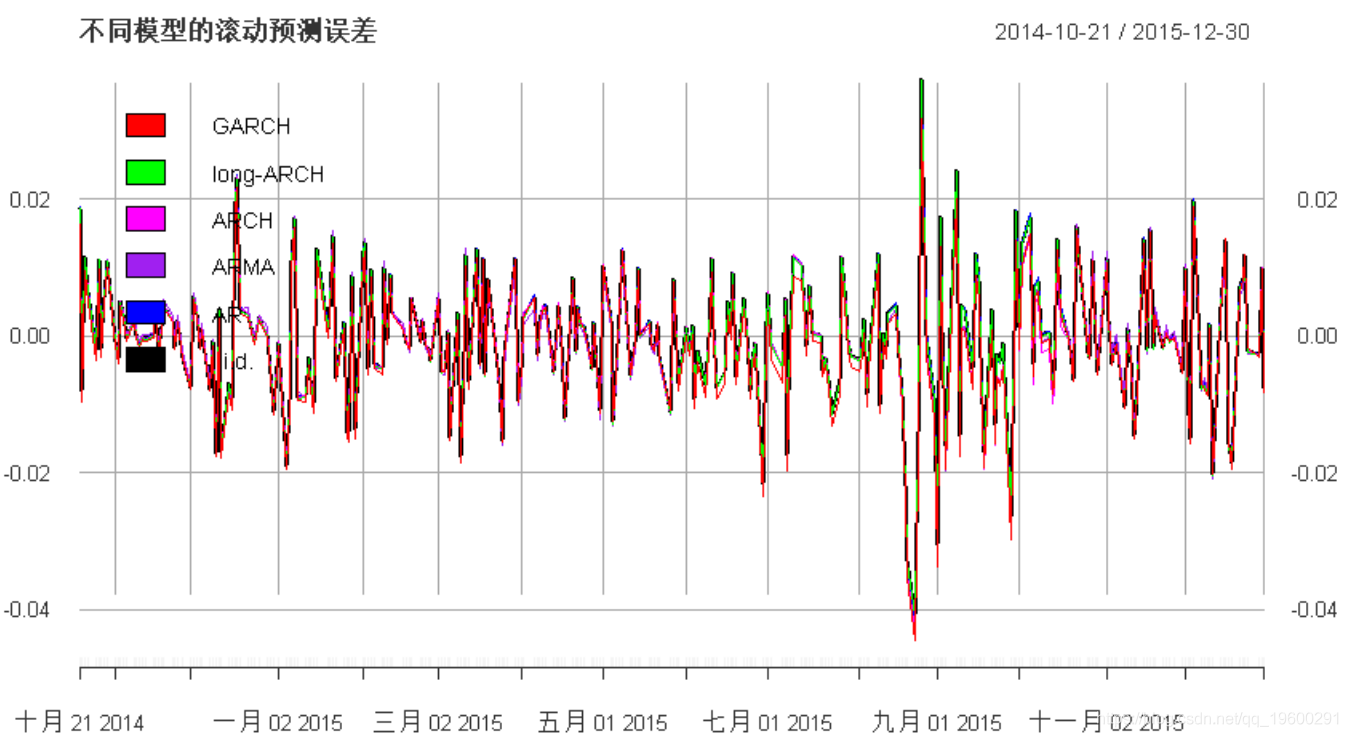
我们看到，现在所有模型都拟合了时间序列。此外，我们在模型之间没有发现任何显着差异。

我们最终可以比较静态误差和滚动误差：
1. barplot(rbind(error_var[, "out-of-sample"], rolling_error_var[, "out-of-sample"])
2. col = c("darkblue", "darkgoldenrod"),
3. legend = c("静态预测", "滚动预测"),
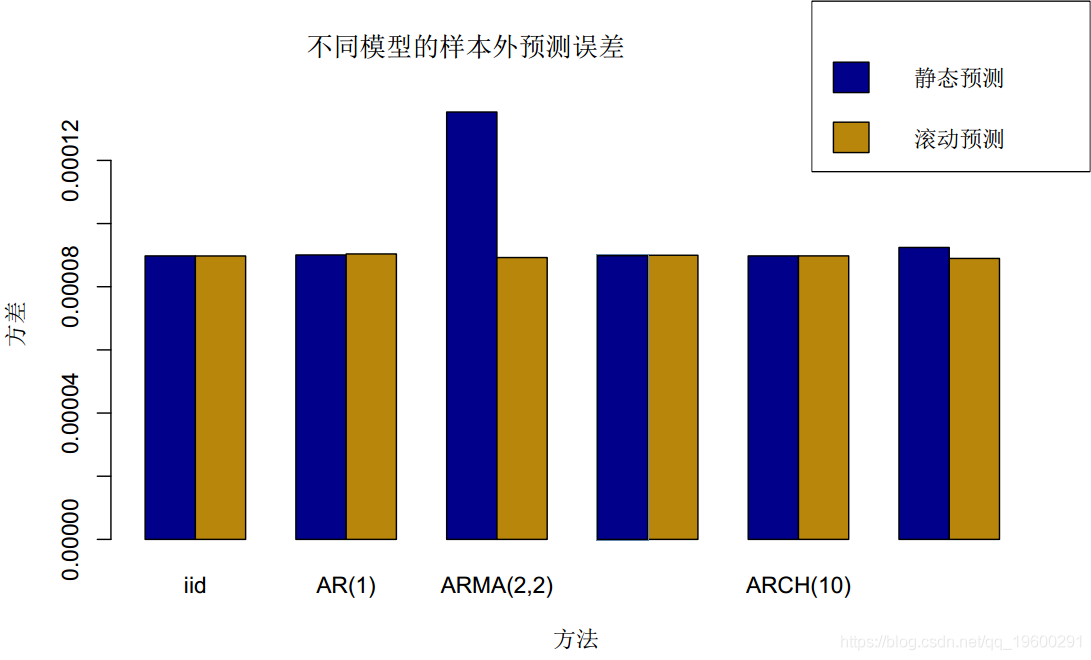
我们可以看到，滚动预测在某些情况下是必须的。因此，实际上，我们需要定期进行滚动预测改进。

方差模型

 ARCH和GARCH模型

对数收益率残差wt的ARCH（m）模型为

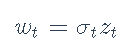
其中zt是具有零均值和恒定方差的白噪声序列，而条件方差σ2t建模为

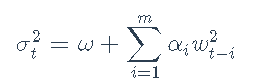
其中，m为模型阶数，ω> 0，αi≥0为参数。

GARCH（m，s）模型使用σ2t上的递归项扩展了ARCH模型：

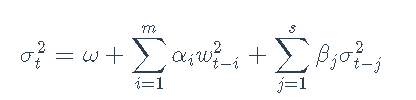
其中参数ω> 0，αi≥0，βj≥0需要满足∑mi =1αi+ ∑sj = 1βj≤1的稳定性。

rugarch生成数据

首先，我们需要定义模型：
2. #指定具有给定系数和参数的GARCH模型
4. #>
5. #> *---------------------------------*
6. #> * GARCH Model Spec *
7. #> *---------------------------------*
8. #>
9. #> Conditional Variance Dynamics
10. #> ------------------------------------
11. #> GARCH Model : sGARCH(1,1)
12. #> Variance Targeting : FALSE
13. #>
14. #> Conditional Mean Dynamics
15. #> ------------------------------------
16. #> Mean Model : ARFIMA(1,0,0)
17. #> Include Mean : TRUE
18. #> GARCH-in-Mean : FALSE
19. #>
20. #> Conditional Distribution
21. #> ------------------------------------
22. #> Distribution : norm
23. #> Includes Skew : FALSE
24. #> Includes Shape : FALSE
25. #> Includes Lambda : FALSE
27. #> Level Fixed Include Estimate LB UB
28. #> mu 0.005 1 1 0 NA NA
29. #> ar1 -0.900 1 1 0 NA NA
30. #> ma 0.000 0 0 0 NA NA
31. #> arfima 0.000 0 0 0 NA NA
32. #> archm 0.000 0 0 0 NA NA
33. #> mxreg 0.000 0 0 0 NA NA
34. #> omega 0.001 1 1 0 NA NA
35. #> alpha1 0.300 1 1 0 NA NA
36. #> beta1 0.650 1 1 0 NA NA
37. #> gamma 0.000 0 0 0 NA NA
38. #> eta1 0.000 0 0 0 NA NA
39. #> eta2 0.000 0 0 0 NA NA
40. #> delta 0.000 0 0 0 NA NA
41. #> lambda 0.000 0 0 0 NA NA
42. #> vxreg 0.000 0 0 0 NA NA
43. #> skew 0.000 0 0 0 NA NA
44. #> shape 0.000 0 0 0 NA NA
45. #> ghlambda 0.000 0 0 0 NA NA
46. #> xi 0.000 0 0 0 NA NA
48. #> $mu
49. #> [1] 0.005
50. #>
51. #> $ar1
52. #> [1] -0.9
53. #>
54. #> $omega
55. #> [1] 0.001
56. #>
57. #> $alpha1
58. #> [1] 0.3
59. #>
60. #> $beta1
61. #> [1] 0.65
63. true_params
64. #> mu ar1 omega alpha1 beta1
65. #> 0.005 -0.900 0.001 0.300 0.650
然后，我们可以生成收益率时间序列：
1. # 模拟一条路径
3. hpath(garch_spec, n.sim = T)
5. #> num [1:2000, 1] 0.167 -0.217
7. # 绘图对数收益
9. { plot(synth_log_returns, main = "GARCH模型的对数收益", lwd = 1.5)
10. lines(synth_volatility
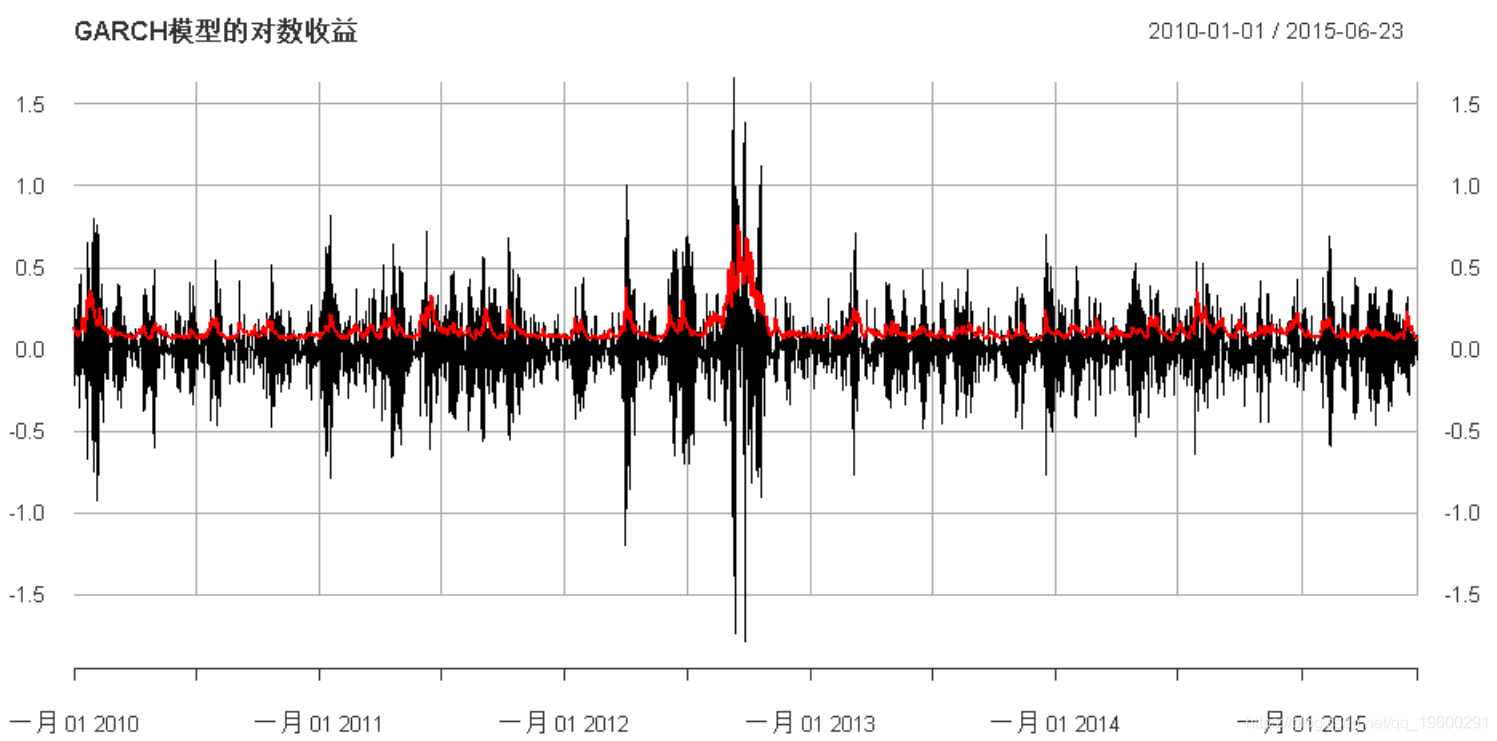
GARCH

现在，我们可以估计参数：
1. # 指定一个GARCH模型
2. ugarchspec(mean.model = list(armaOrder = c(1,0)
4. # 估计模型
6. coef(garch_fit)
7. #> mu ar1 omega alpha1 beta1
8. #> 0.0036510100 -0.8902333595 0.0008811434 0.2810460728 0.6717486402
11. #> mu ar1 omega alpha1 beta1
12. #> 0.005 -0.900 0.001 0.300 0.650
14. # 系数误差
16. #> mu ar1 omega alpha1 beta1
17. #> 0.0013489900 0.0097666405 0.0001188566 0.0189539272 0.0217486402
我们还可以研究样本数量T对参数估计误差的影响：
1. # 循环
3. for (T_ in T_sweep) {
4. garch_fit
5. error_coeffs_vs_T <- rbind(error_coeffs_vs_T, abs((coef(garch_fit) - true_params)/true_params))
6. estim_coeffs_vs_T <- rbind(estim_coeffs_vs_T, coef(garch_fit))
9. # 绘图
10. matplot(T_sweep, 100*error_coeffs_vs_T,
11. main = "估计GARCH系数的相对误差", xlab = "T", ylab = "误差 (%)",
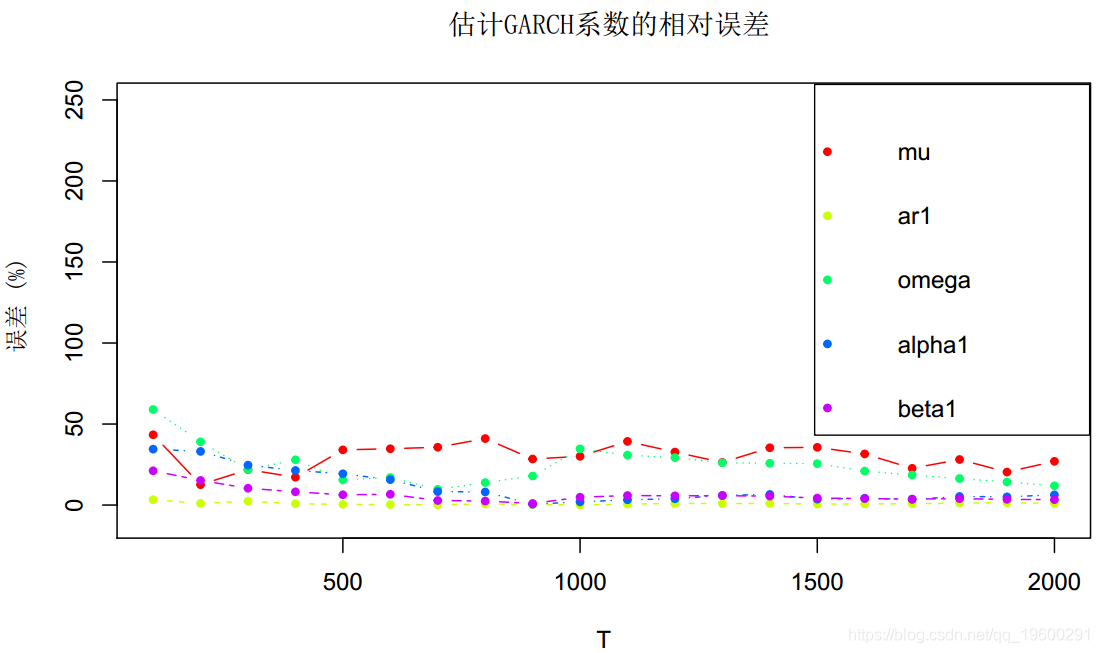
真实的ω几乎为零，因此误差非常不稳定。至于其他系数，就像在ARMA情况下一样，μ的估计确实很差（相对误差超过50％），而其他系数似乎在T = 800个样本后得到了很好的估计。

GARCH结果比较

作为健全性检查，我们现在将比较两个软件包 fGarch 和 rugarch的结果：
2. # 指定具有特定参数值的ARMA（0,0）-GARCH（1,1）作为数据生成过程
3. garch_spec
5. #生成长度为1000的数据
7. path(garch_fixed_spec, n.sim = 1000)@path$
9. # 使用“ rugarch”包指定和拟合模型
11. rugarch_fit <- ugarchfit(spec = garch_spec, data = x)
13. # 使用包“ fGarch”拟合模型
14. garchFit(formula = ~ garch(1, 1), data = x, trace = FALSE)
16. # 比较模型系数
17. #> mu omega alpha1 beta1
18. #> 0.09749904 0.01395109 0.13510445 0.73938595
19. #> mu omega alpha1 beta1
20. #> 0.09750394 0.01392648 0.13527024 0.73971658
22. # 比较拟合的标准偏差
23. print(head(fGarch_fi
24. #> [1] 0.3513549 0.3254788 0.3037747 0.2869034 0.2735266 0.2708994
25. print(head(rugar
26. #> [1] 0.3538569 0.3275037 0.3053974 0.2881853 0.2745264 0.2716555
确实，这两个软件包给出了相同的结果。

使用rugarch包进行GARCH预测

一旦估计出GARCH模型的参数，就可以使用该模型预测未来的值。例如，基于过去的信息对条件方差的单步预测为

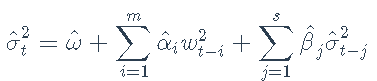
给定ω^ /（1-∑mi =1α^ i-∑sj =1β^ j）。软件包 rugarch 使对样本外数据的预测变得简单：
1. # 估计模型，不包括样本外
4. garch_fit
5. coef(garch_fit)
6. #> mu ar1 omega alpha1 beta1
7. #> 0.0034964331 -0.8996287630 0.0006531088 0.3058756796 0.6815452241
9. # 预测整个样本的对数收益
11. garch_fore@forecast$sigmaFor[1, ]
13. # 对数收益图
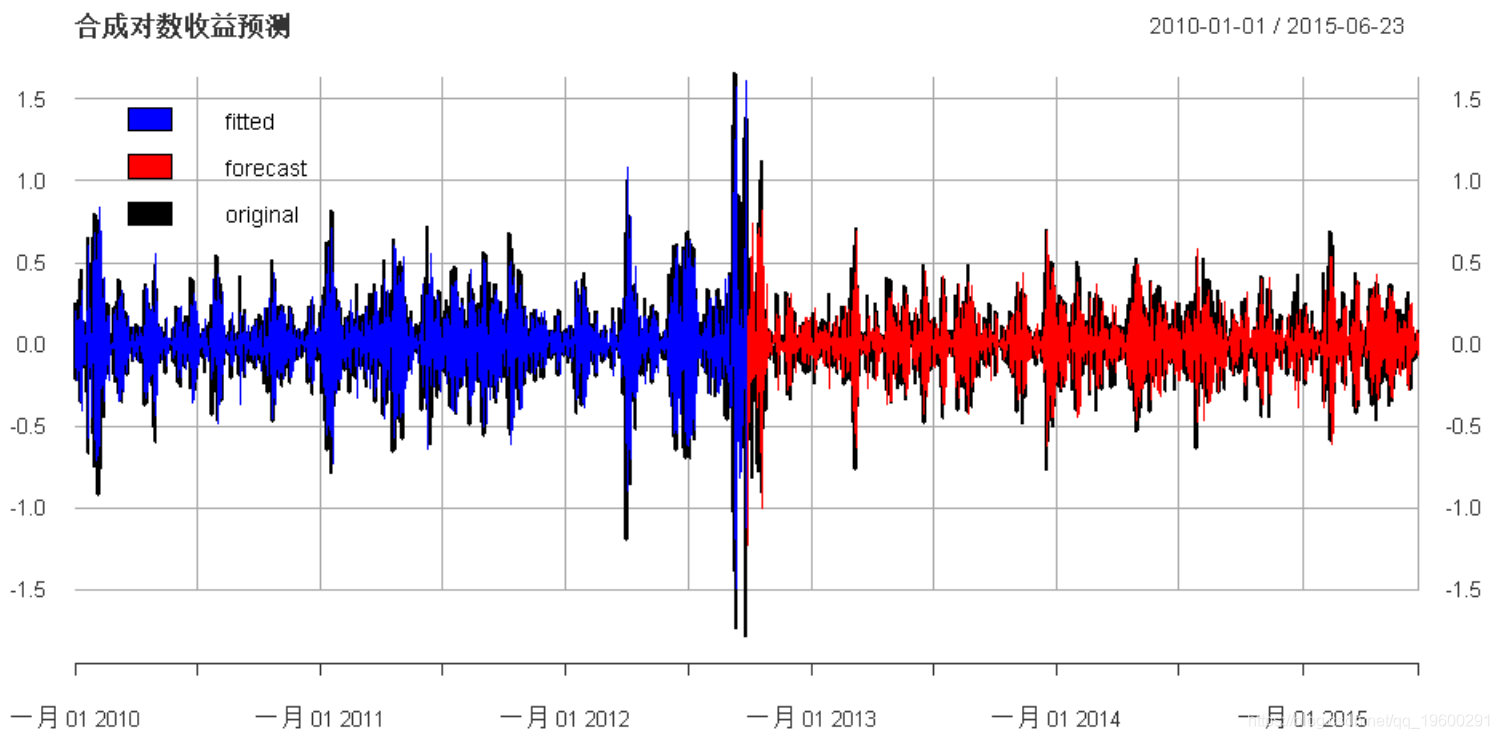
14. plot(cbind("fitted" = fitted(garch_fit),
15. main = "合成对数收益预测", legend.loc = "topleft")
1. #波动率对数收益图
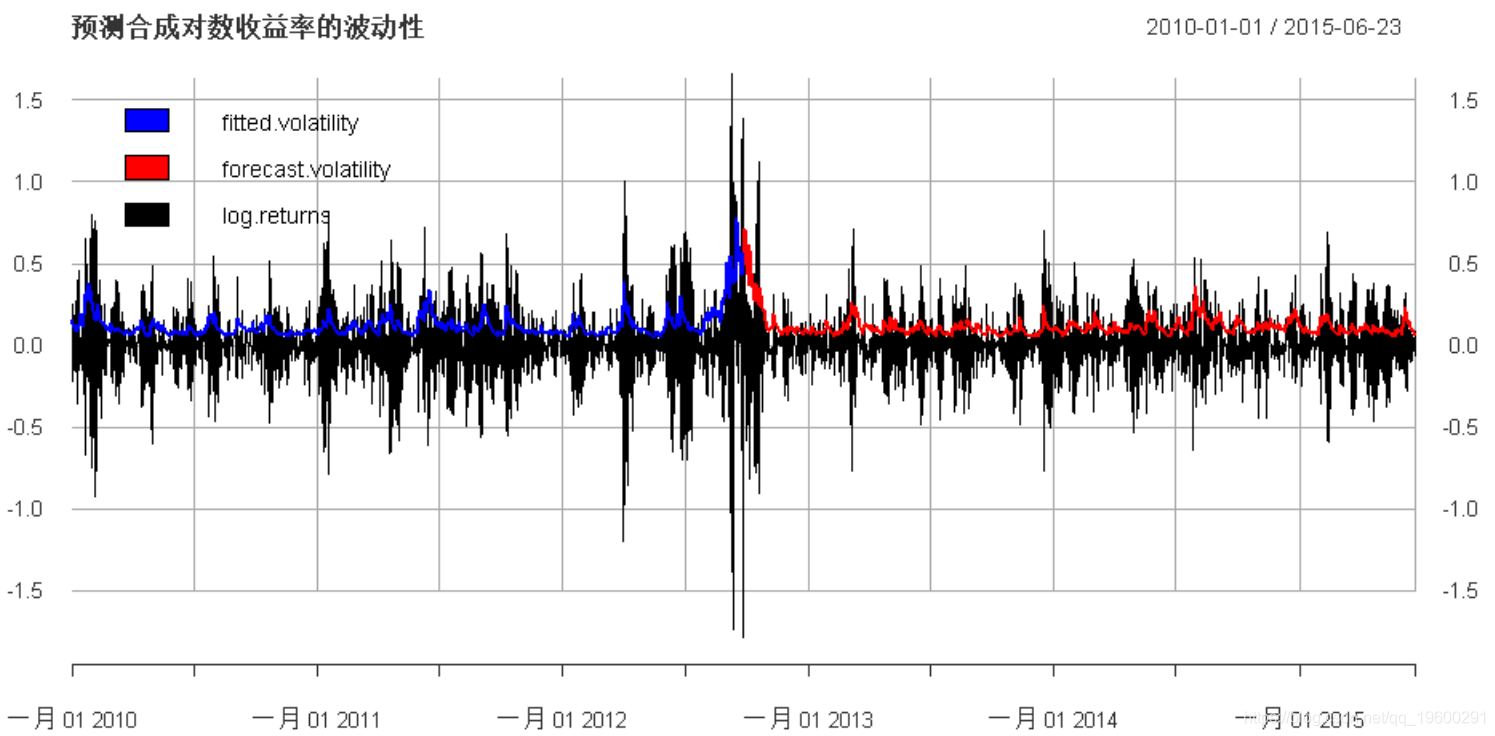
2. plot(cbind("fitted volatility" = sigma(garch_fit),
3. main = "预测合成对数收益率的波动性", legend.loc = "topleft")
不同方法

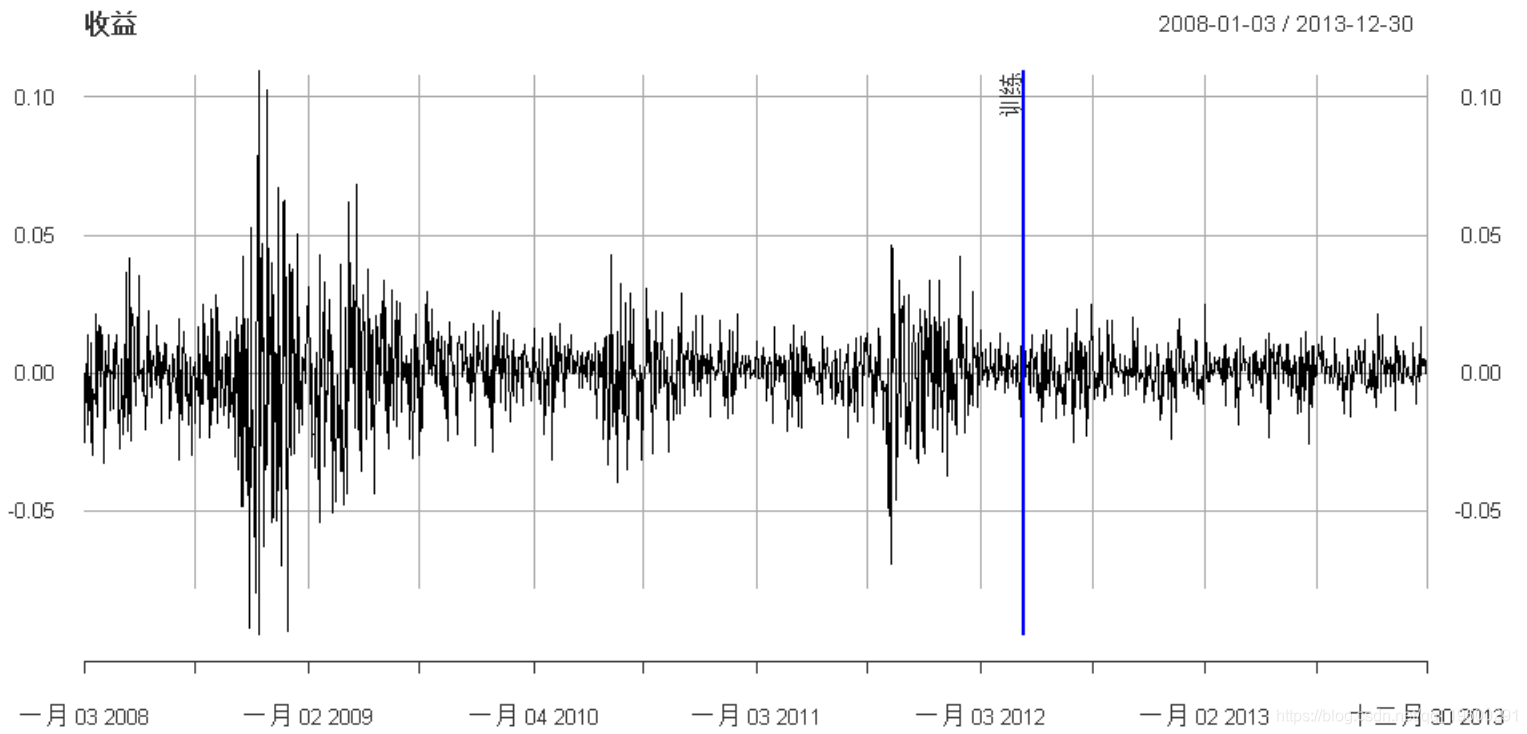
让我们首先加载S＆P500：
3. # 加载标准普尔500指数数据
5. head(SP500_index_prices)
6. #> SP500
7. #> 2008-01-02 1447.16
8. #> 2008-01-03 1447.16
9. #> 2008-01-04 1411.63
10. #> 2008-01-07 1416.18
11. #> 2008-01-08 1390.19
12. #> 2008-01-09 1409.13
14. # 准备训练和测试数据
16. x_trn <- x[1:T_trn]
17. x_tst <- x[-c(1:T_trn)]
19. # 绘图
20. { plot(x, main = "收益"
21. addEventLines(xts("训练", in
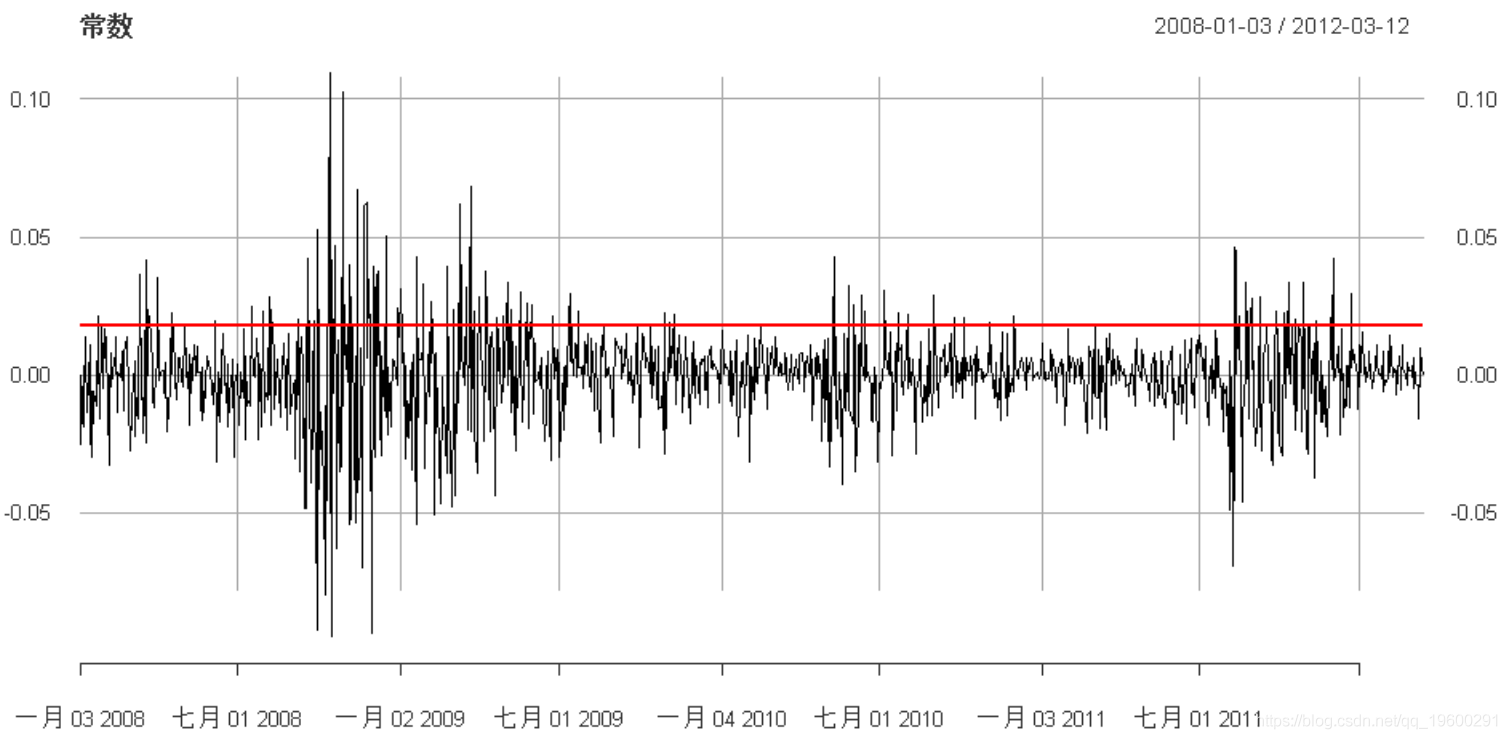
常数

让我们从常数开始：
1. plot(cbind(sqrt(var_constant), x_trn)
2. main = "常数")
移动平均值

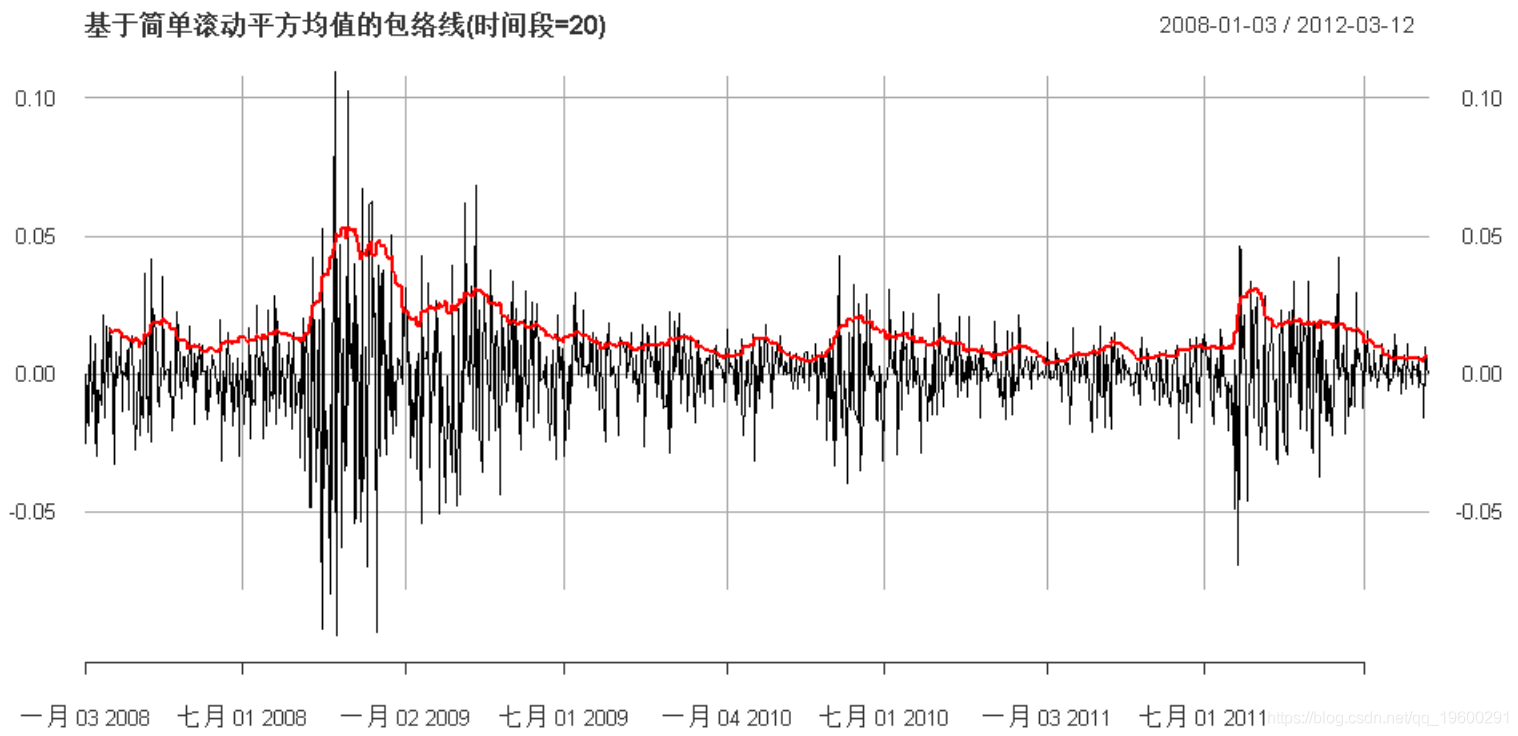
现在，让我们使用平方收益的移动平均值：
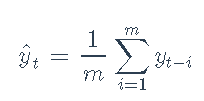
2. plot(cbind(sqrt(var_t), x_trn),
3. main = "基于简单滚动平方均值的包络线(时间段=20)
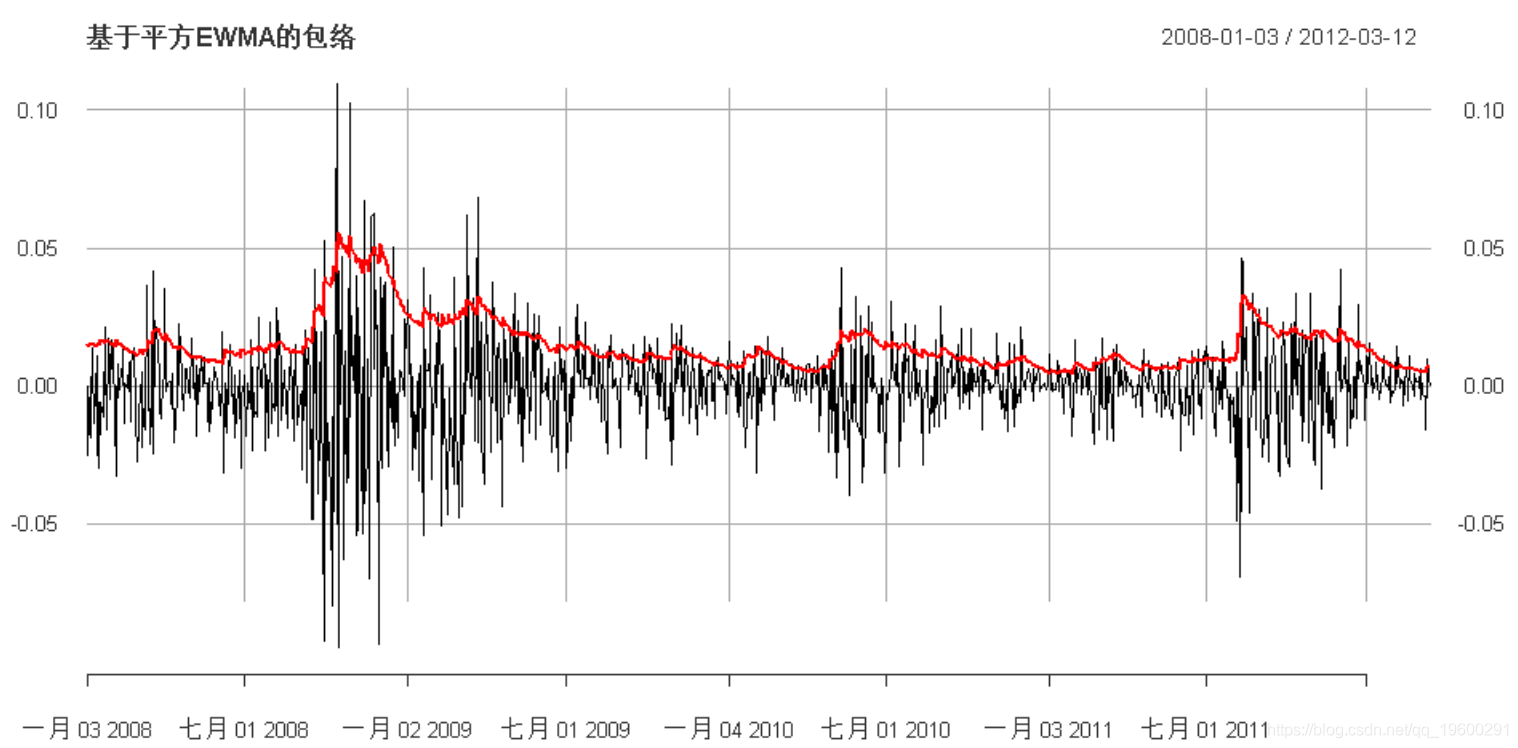
EWMA

指数加权移动平均线（EWMA）：

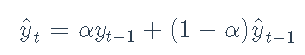
请注意，这也可以建模为ETS（A，N，N）状态空间模型：
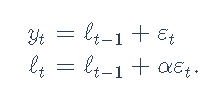
2. plot(cbind(std_t, x_trn),
3. main = "基于平方EWMA的包络")
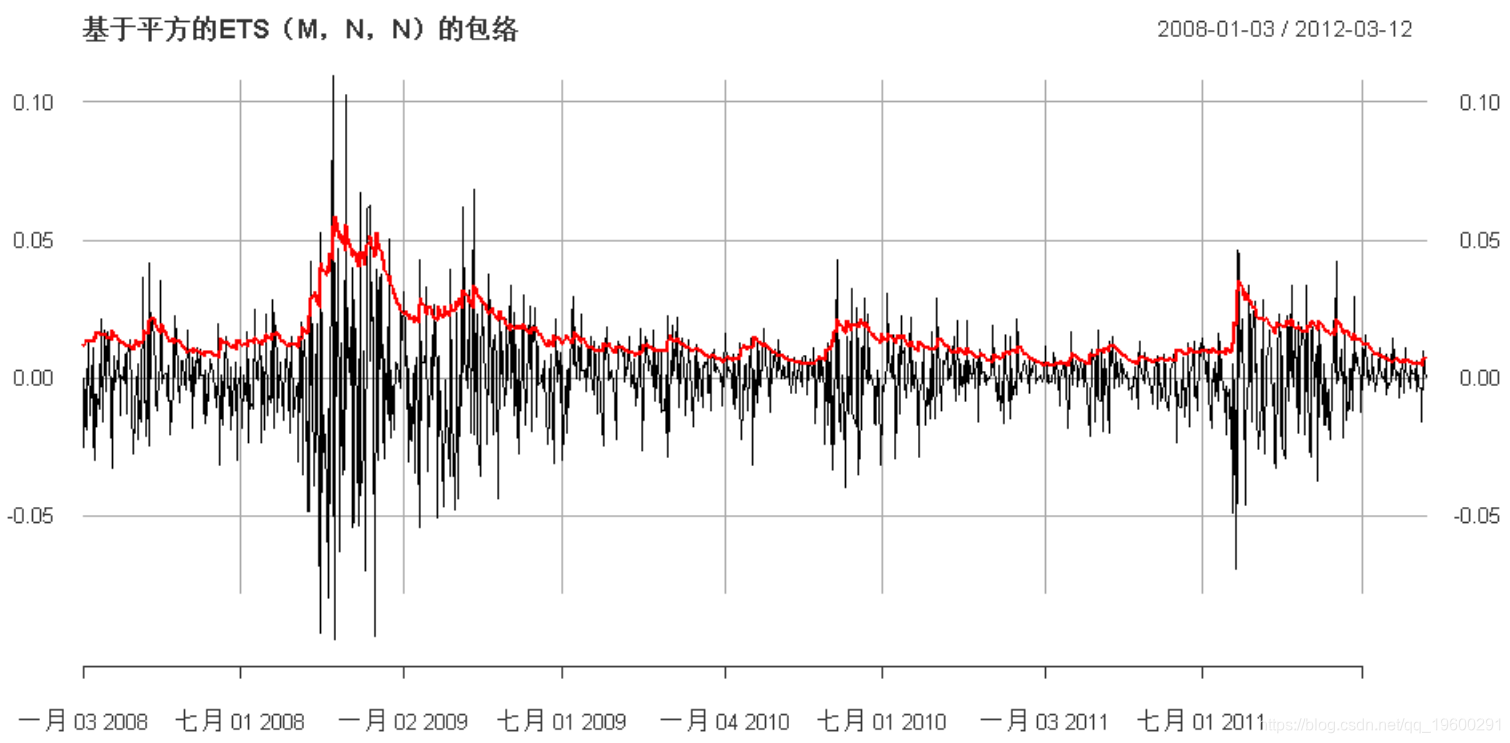
乘法ETS

我们还可以尝试ETS模型的不同变体。例如，具有状态空间模型的乘性噪声版本ETS（M，N，N）：
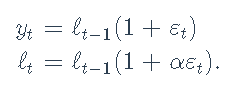
2. plot(cbind(std_t, x_trn), col = c("red", "black")
3. main = "基于平方的ETS（M，N，N）的包络"
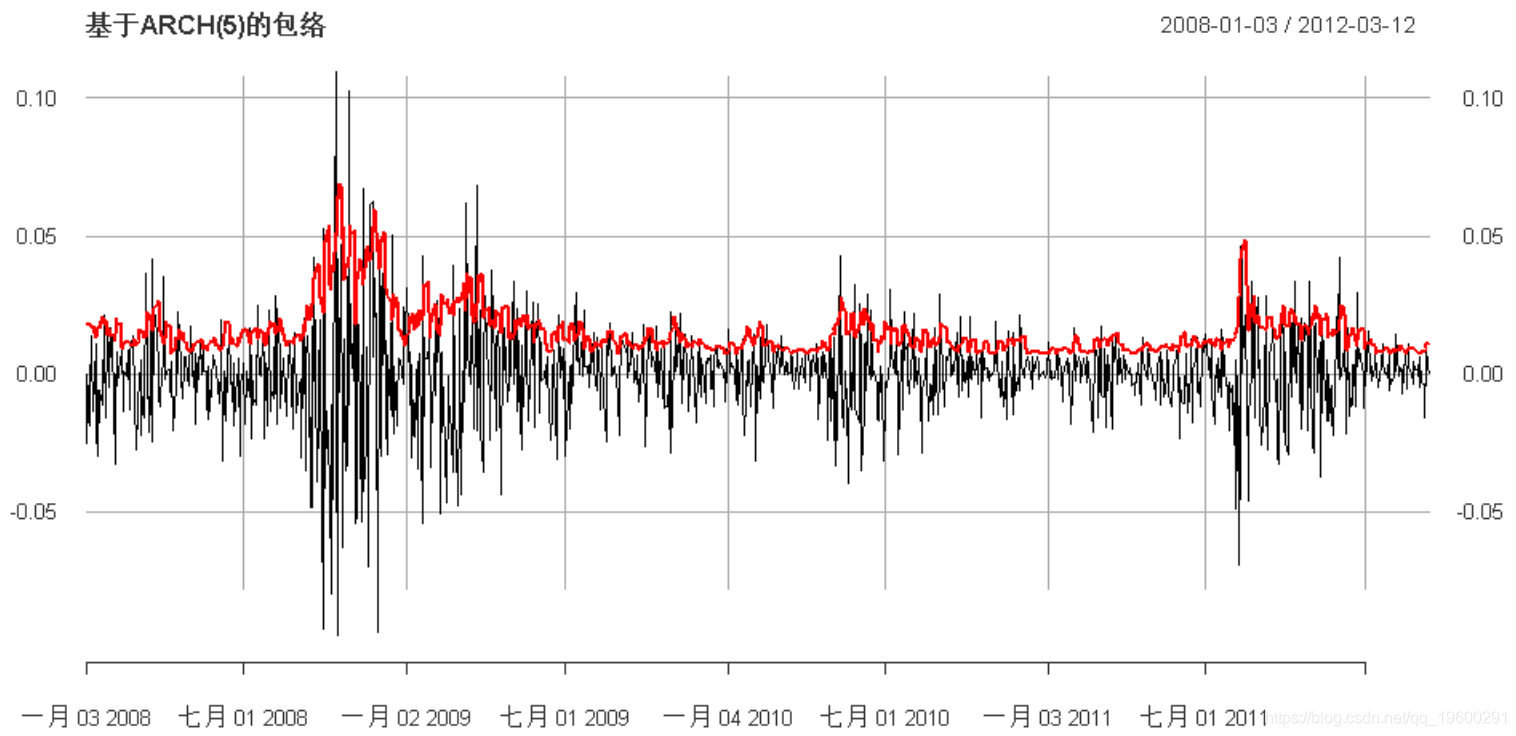
ARCH

现在，我们可以使用更复杂的ARCH建模：
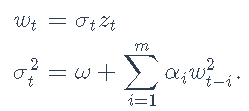
2. plot(cbind(std_t, x_trn), col = c("red", "black")
3. main = "基于ARCH(5)的包络")
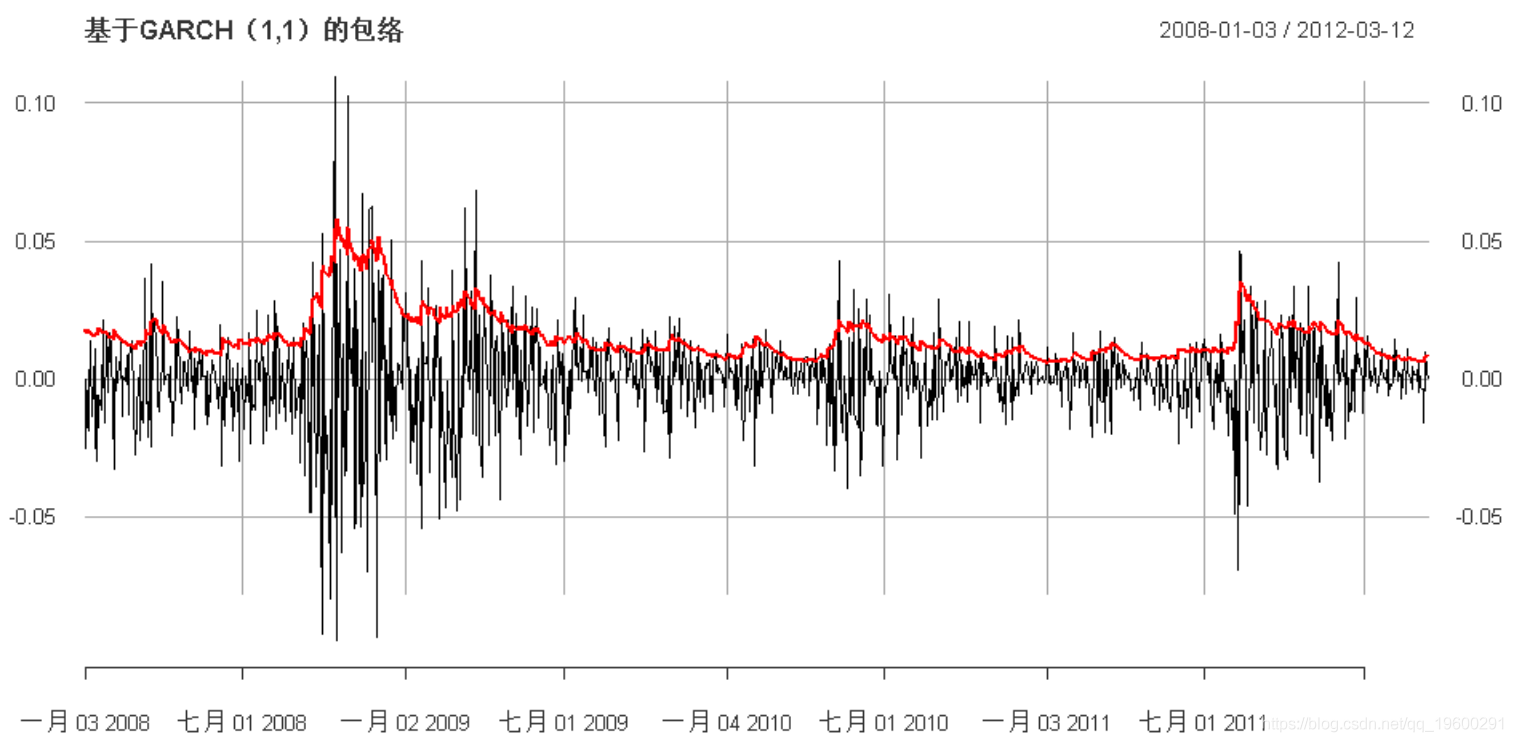
GARCH

我们可以将模型提升到GARCH：
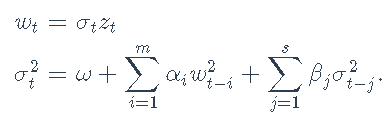
2. plot(cbind(std_t, x_trn), col = c("red", "black")
3. main = "基于GARCH（1,1）的包络")
SV随机波动率

最后，我们可以使用随机波动率建模：

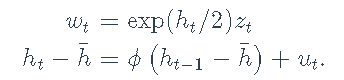
或者，等效地，
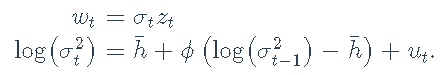
2. plot(cbind(std_t, x_trn), col = c("red", "black"),
3. main = "基于随机波动率的包络分析")
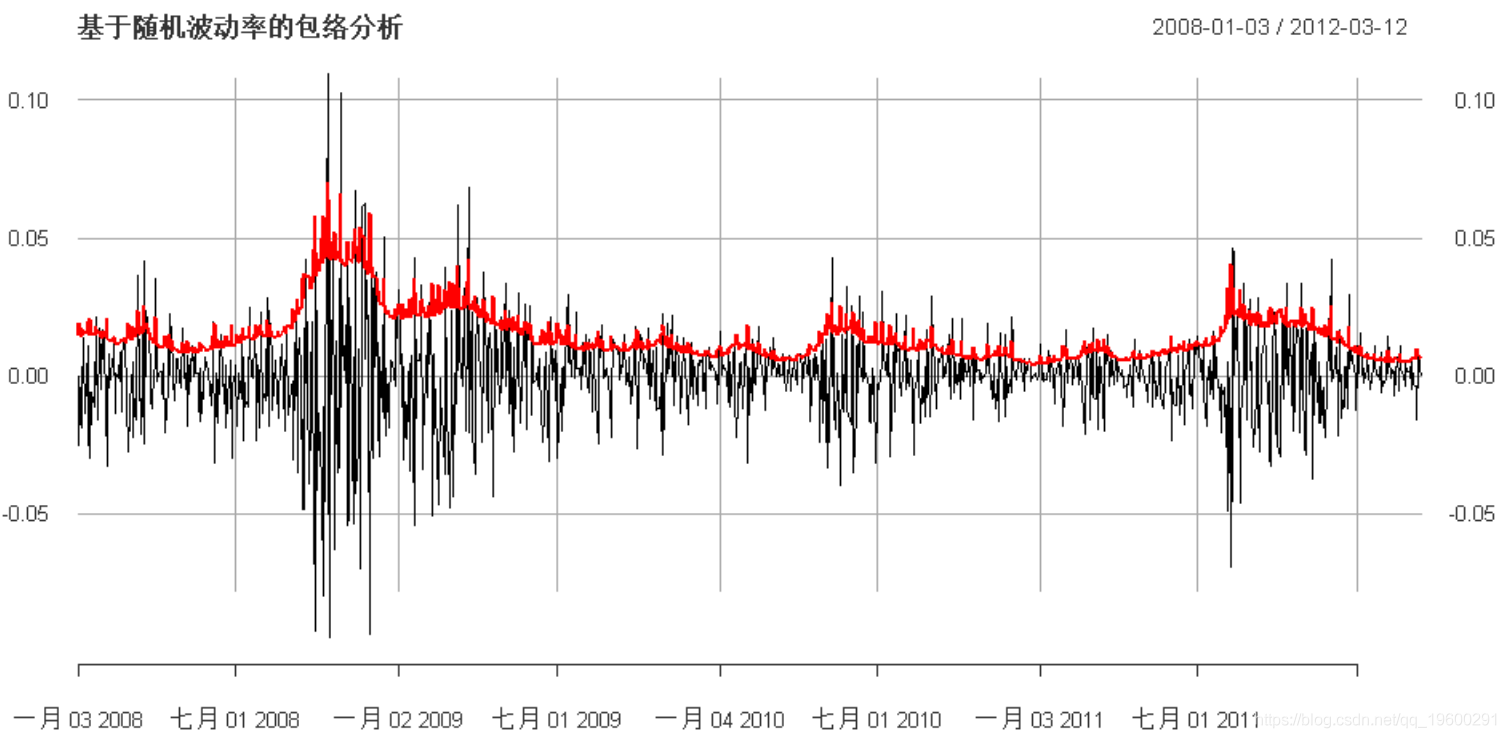
比较

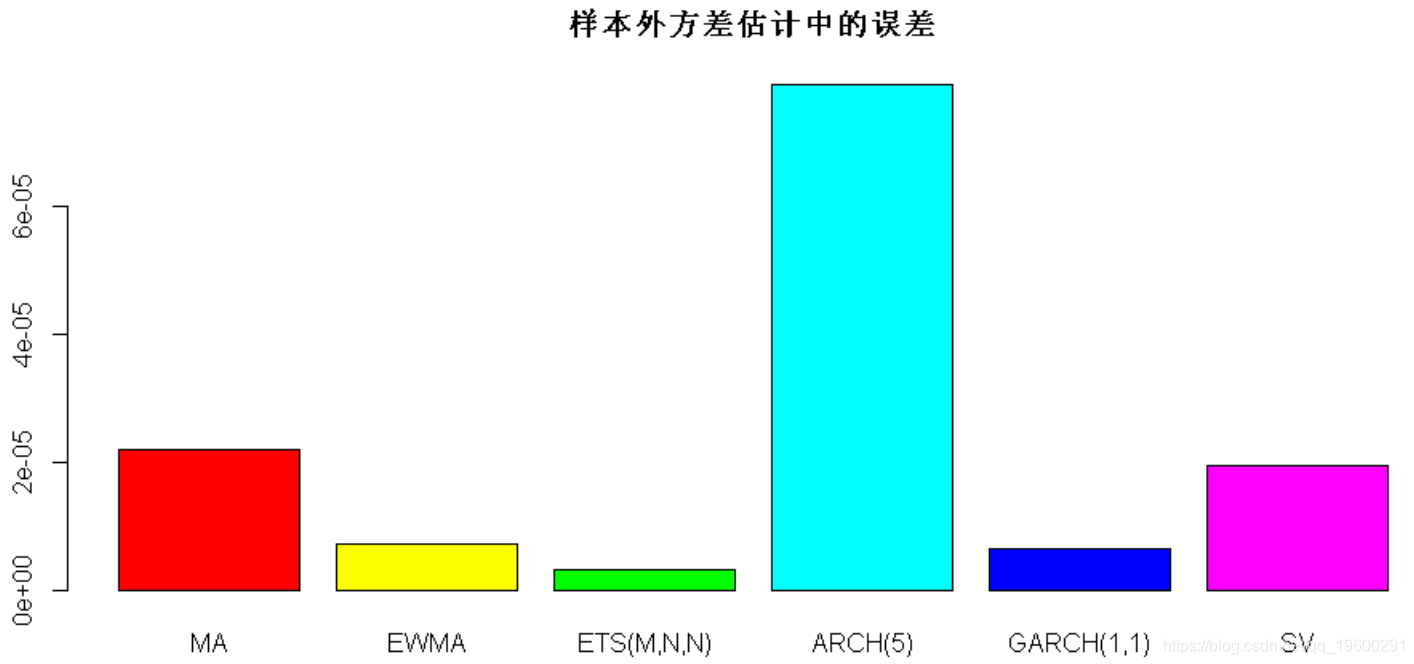
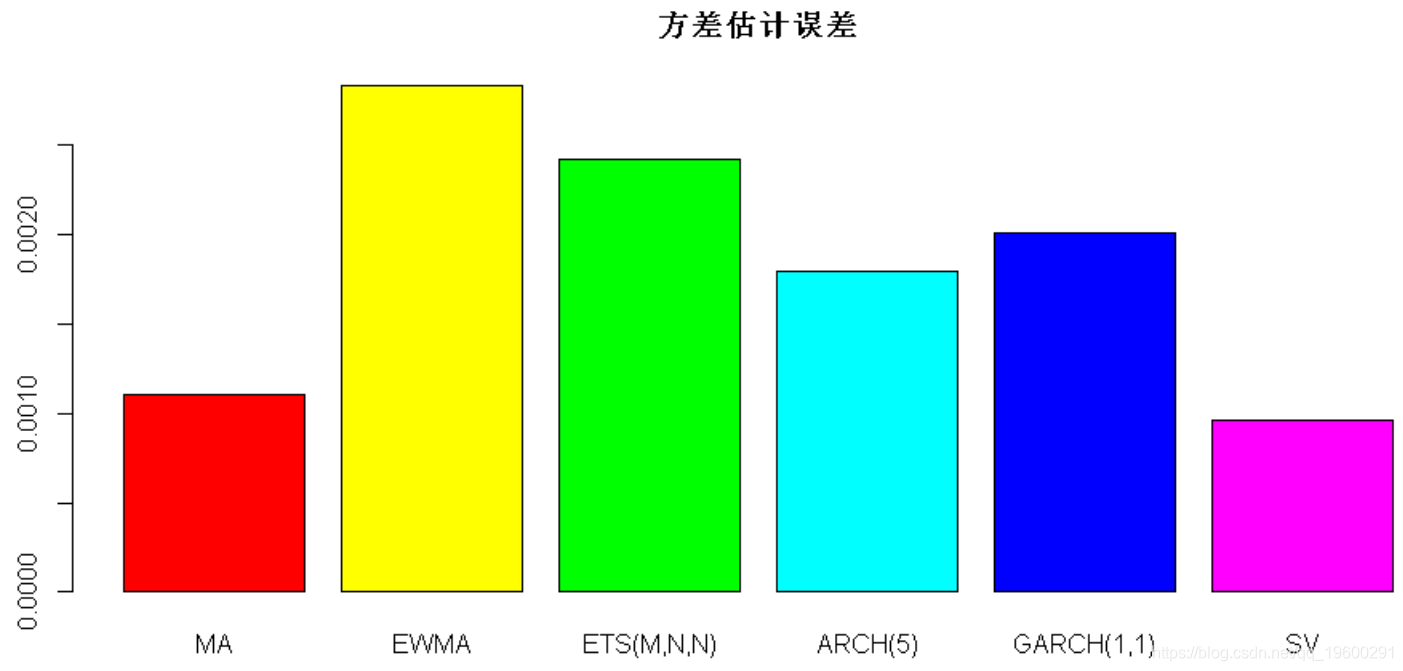
现在，我们可以比较每种方法在样本外期间的方差估计中的误差：
2. #> MA EWMA ETS(M,N,N) ARCH(5) GARCH(1,1) SV
3. #> 2.204965e-05 7.226188e-06 3.284057e-06 7.879039e-05 6.496545e-06 6.705059e-06
4. barplot(error_all, main = "样本外方差估计中的误差"
滚动窗口比较

六种方法的滚动窗口比较：MA，EWMA，ETS（MNN），ARCH（5），GARCH（1,1）和SV。
2. #滚动窗口
3. lookback <- 200
4. len_tst <- 40
5. for (i in seq(lookback, T-len_tst, by = len_tst)) {
7. # MA
8. var_t <- roll_meanr(x_trn^2, n = 20, fill = NA)
9. var_fore <- var(x_trn/sqrt(var_t), na.rm = TRUE) * tail(var_t, 1)
10. error_ma <- c(error_ma, abs(var_fore - var_tst))
12. # EWMA
14. error_ewma <- c(error_ewma, abs(var_fore - var_tst))
16. # ETS(M,N,N)
18. error_ets_mnn <- c(error_ets_mnn, abs(var_fore - var_tst))
20. # ARCH
22. error_arch <- c(error_arch, abs(var_fore - var_tst))
24. # GARCH
26. error_garch <- c(error_garch, abs(var_fore - var_tst))
28. # SV
30. error_sv <- c(error_sv, abs(var_fore - var_tst))
31. }
34. barplot(error_all, main = "方差估计误差",
多元GARCH模型

出于说明目的，我们将仅考虑恒定条件相关（CCC）和动态条件相关（DCC）模型，因为它们是最受欢迎的模型。对数收益率残差wt建模为

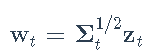
其中zt是具有零均值和恒定协方差矩阵II的iid白噪声序列。条件协方差矩阵Σt建模为

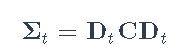
其中Dt = Diag（σ1，t，...，σN，t）是标准化噪声向量C，协方差矩阵ηt=C-1wt（即，它包含等于1的对角线元素）。

基本上，使用此模型，对角矩阵Dt包含一组单变量GARCH模型，然后矩阵C包含序列之间的一些相关性。该模型的主要缺点是矩阵C是恒定的。为了克服这个问题，DCC被提议为

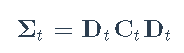
其中Ct包含等于1的对角元素。要强制等于1的对角元素，Engle将其建模为

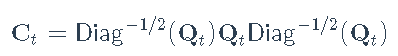
Qt具有任意对角线元素并遵循模型

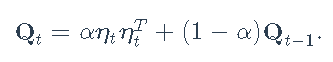
我们将生成数据，估计参数和预测。

从加载多元ETF数据开始：
- SPDR S＆P 500 ETF
- 20年以上国债ETF
- IEF：7-10年期国债ETF
2. # 下载数据
3. prices <- xts()
5. head(prices)
6. #> SPY TLT IEF
7. #> 2013-01-02 127.8779 99.85183 93.65224
8. #> 2013-01-03 127.5890 98.49886 93.17085
9. #> 2013-01-04 128.1493 98.88306 93.21463
10. #> 2013-01-07 127.7991 98.92480 93.26714
11. #> 2013-01-08 127.4314 99.57622 93.49468
12. #> 2013-01-09 127.7553 99.48438 93.54719
14. # 绘制三个对数价格序列
15. plot(log(prices)
16. main = "三个ETF的对数价格", legend.loc = "topleft")
首先，我们定义模型：
3. # 指定i.i.d.单变量时间序列模型
4. ugarch_spec
5. # 指定DCC模型
6. spec( multispec(replicate(spec, n = 3))
接下来，我们拟合模型：
1. # 估计模型
3. #>
4. #> *---------------------------------*
5. #> * DCC GARCH Fit *
6. #> *---------------------------------*
7. #>
8. #> Distribution : mvnorm
9. #> Model : DCC(1,1)
10. #> No. Parameters : 44
11. #> [VAR GARCH DCC UncQ] : [30+9+2+3]
12. #> No. Series : 3
13. #> No. Obs. : 1007
14. #> Log-Likelihood : 12198.4
15. #> Av.Log-Likelihood : 12.11
16. #>
17. #> Optimal Parameters
18. #> -----------------------------------
19. #> Estimate Std. Error t value Pr(>|t|)
20. #> [SPY].omega 0.000004 0.000000 11.71585 0.000000
21. #> [SPY].alpha1 0.050124 0.005307 9.44472 0.000000
22. #> [SPY].beta1 0.870051 0.011160 77.96041 0.000000
23. #> [TLT].omega 0.000001 0.000001 0.93156 0.351563
24. #> [TLT].alpha1 0.019716 0.010126 1.94707 0.051527
25. #> [TLT].beta1 0.963760 0.006434 149.79210 0.000000
26. #> [IEF].omega 0.000000 0.000001 0.46913 0.638979
27. #> [IEF].alpha1 0.031741 0.023152 1.37097 0.170385
28. #> [IEF].beta1 0.937777 0.016498 56.84336 0.000000
29. #> [Joint]dcca1 0.033573 0.014918 2.25044 0.024421
30. #> [Joint]dccb1 0.859787 0.079589 10.80278 0.000000
31. #>
32. #> Information Criteria
33. #> ---------------------
34. #>
35. #> Akaike -24.140
36. #> Bayes -23.925
37. #> Shibata -24.143
38. #> Hannan-Quinn -24.058
39. #>
40. #>
41. #> Elapsed time : 0.8804049
我们可以绘制时变相关性：
1. # 提取时变协方差和相关矩阵
2. dim(dcc_cor)
3. #> [1] 3 3 1007
5. #绘图
7. plot(corr_t
8. main = "时变相关", legend.loc = "left")
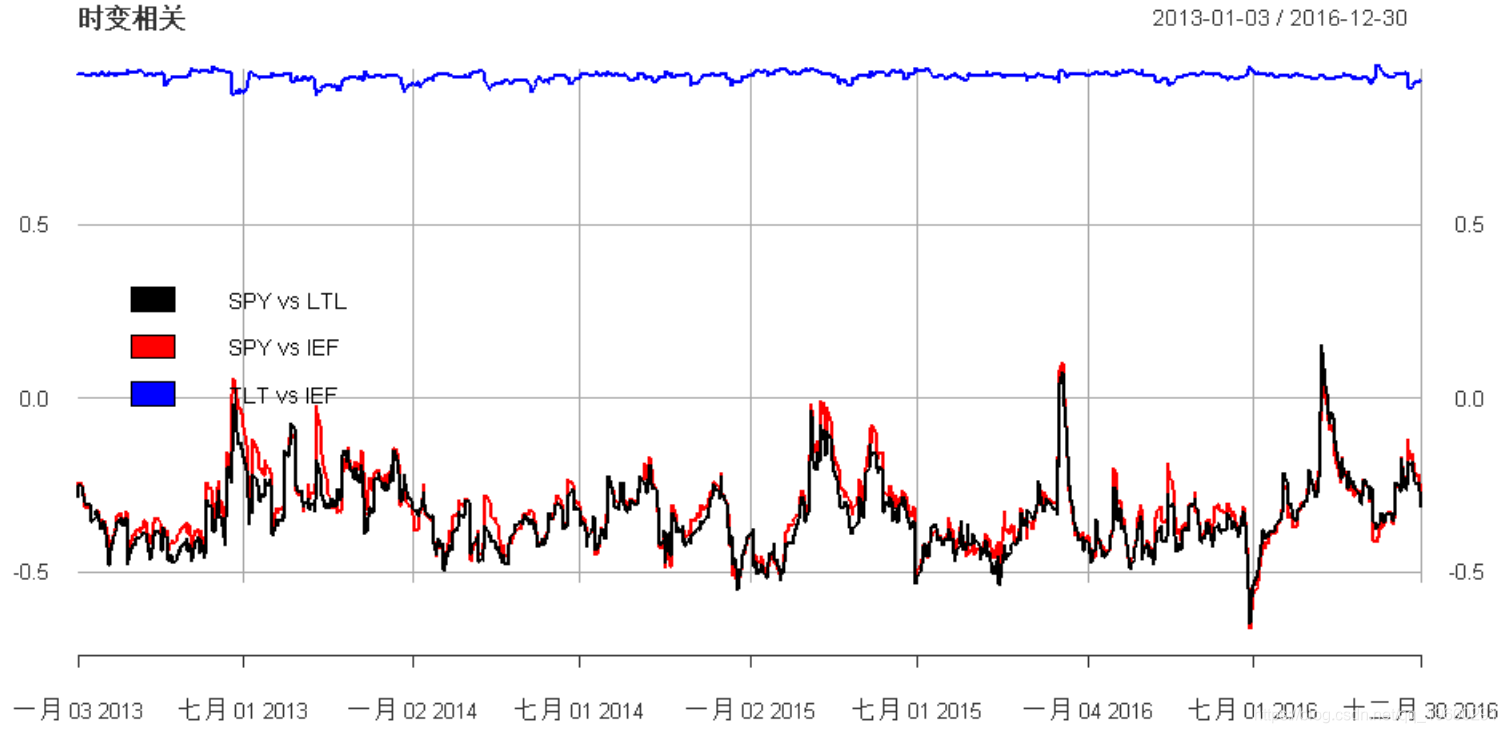
我们看到两个收益ETF之间的相关性非常高且相当稳定。与SPY的相关性较小，在小于0的区间波动。

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.GARCH（1,1），MA以及历史模拟法的VaR比较

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.matlab预测ARMA-GARCH 条件均值和方差模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略
▍关注我们【大数据部落】第三方数据服务提供商,提供全面的统计分析与数据挖掘咨询服务,为客户定制个性化的数据解决方案与行业报告等。 ▍咨询链接：http://y0.cn/teradat ▍联系邮箱：3025393450@qq.com
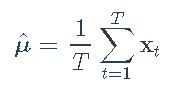
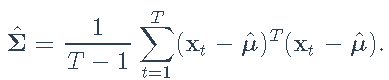
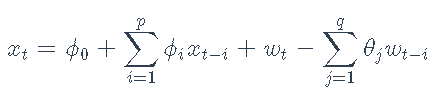
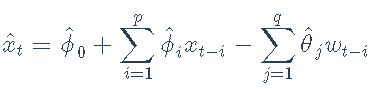
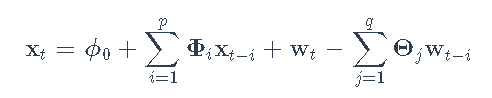
相关阅读:
Gitblit 的安装使用
 PLSQL 美化规则文件详解
 SQL Server Agent的作用
 使用C#创建Widows服务
 关于VS编译DevExpress默认产生几个多余的语言包的问题解决
 （转）查询A、B表中，A表中存在B表不存在的数据
 子类构造、析构时调用父类的构造、析构函数顺序
 ACCDB与MDB的读取区别
 vue中如何动态添加readonly属性
 windows下生成文件夹目录结构
原文地址：https://www.cnblogs.com/tecdat/p/14397643.html

拓端数据tecdat|R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模

原文链接：http://tecdat.cn/?p=20015

均值模型

iid模型

单变量ARMA模型

rugarch生成数据

ARMA模型

ARMA预测

ARMA模型选择

ARMA预测

多元VARMA模型

比较

滚动窗口比较

方差模型

ARCH和GARCH模型

rugarch生成数据

GARCH

GARCH结果比较

使用rugarch包进行GARCH预测

不同方法

常数

移动平均值

EWMA

乘法ETS

ARCH

GARCH

SV随机波动率

比较

滚动窗口比较

多元GARCH模型