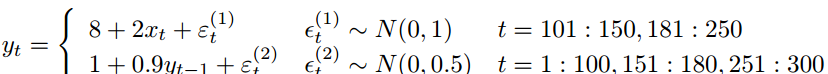原文链接：http://tecdat.cn/?p=12227
摘要
本文描述了R语言中马尔克夫转换模型的分析过程。首先，对模拟数据集进行详细建模。接下来，将马尔可夫转换模型拟合到具有离散响应变量的真实数据集。用于验证对这些数据集建模的不同方法。
模拟实例
示例数据是一个模拟数据集，用于展示如何检测两种不同模式的存在：一种模式中的响应变量高度相关，另一种模式中的响应仅取决于外生变量x。自相关观测值的区间为1到100、151到180 和251到300。每种方案的真实模型为：
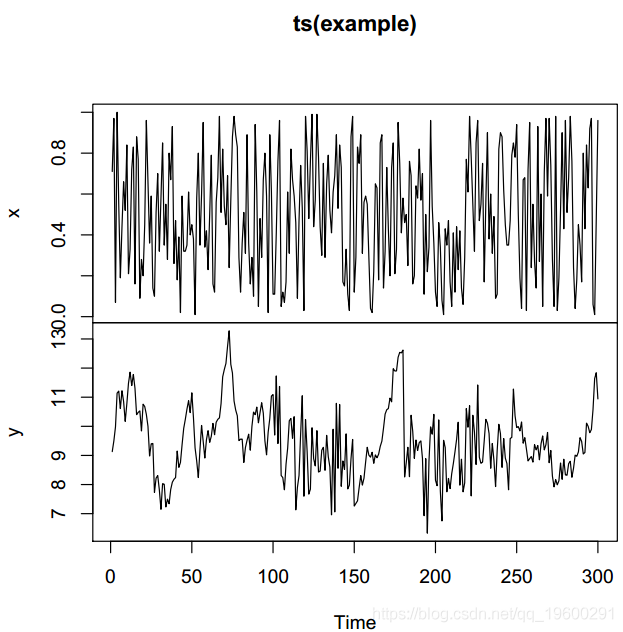
图1中的曲线表明，在不存在自相关的区间中，响应变量y具有与协变量x相似的行为。拟合线性模型以研究协变量x如何解释变量响应y。
> summary(mod)
Call:
lm(formula = y ~ x, data = example)
Residuals:
Min 1Q Median 3Q Max
-2.8998 -0.8429 -0.0427 0.7420 4.0337
> plot(ts(example))
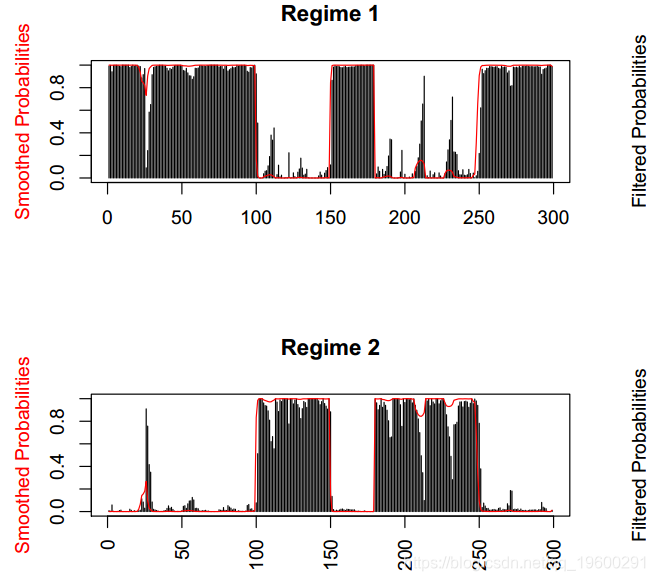
图1：模拟数据，y变量是响应变量
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.0486 0.1398 64.709 < 2e-16 ***
x 0.8235 0.2423 3.398 0.00077 ***
Residual standard error: 1.208 on 298 degrees of freedom
Multiple R-squared: 0.03731, Adjusted R-squared: 0.03408
F-statistic: 11.55 on 1 and 298 DF, p-value: 0.0007701
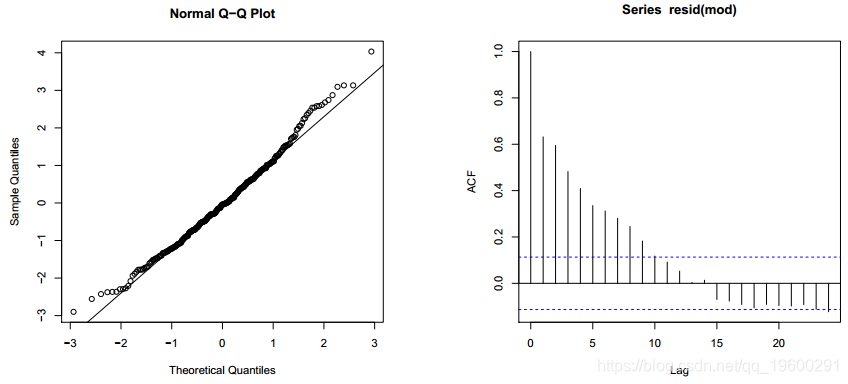
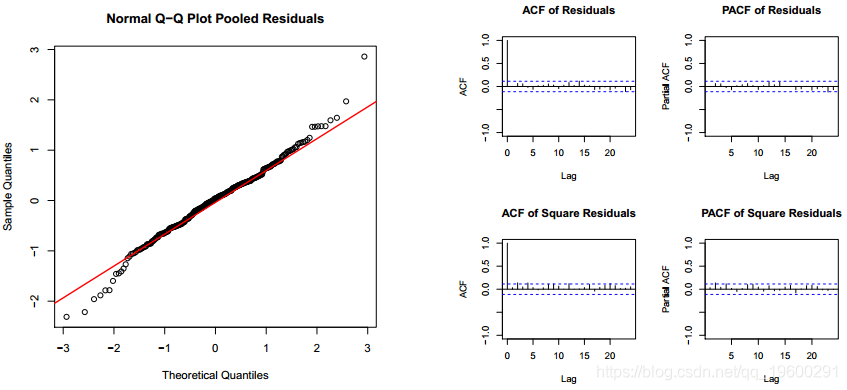
协变量确实很重要，但是模型解释的数据行为非常糟糕。图1中的线性模型残差图表明，它们的自相关很强。残差的诊断图（图2）确认它们似乎不是白噪声，并且具有自相关关系。接下来，将自回归马尔可夫转换模型（MSM-AR）拟合到数据。自回归部分设置为1。为了指示所有参数在两个周期中都可以不同，将转换参数（sw）设置为具有四个分量的矢量。拟合线性模型时的最后一个值称为残差。
标准偏差。有一些选项可控制估算过程，例如用于指示是否完成了过程并行化的逻辑参数。
Markov Switching Model
AIC BIC logLik
637.0736 693.479 -312.5368
Coefficients:
Regime 1
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 0.8417 0.3025 2.7825 0.005394 **
x(S) -0.0533 0.1340 -0.3978 0.690778
y_1(S) 0.9208 0.0306 30.0915 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5034675
Multiple R-squared: 0.8375
Standardized Residuals:
Min Q1 Med Q3 Max
-1.5153666657 -0.0906543311 0.0001873641 0.1656717256 1.2020898986
Regime 2
--------- Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 8.6393 0.7244 11.9261 < 2.2e-16 ***
x(S) 1.8771 0.3107 6.0415 1.527e-09 ***
y_1(S) -0.0569 0.0797 -0.7139 0.4753
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9339683
Multiple R-squared: 0.2408
Standardized Residuals:
Min Q1 Med Q3 Max
-2.31102193 -0.03317756 0.01034139 0.04509105 2.85245598
Transition probabilities:
Regime 1 Regime 2
Regime 1 0.98499728 0.02290884
Regime 2 0.01500272 0.97709116
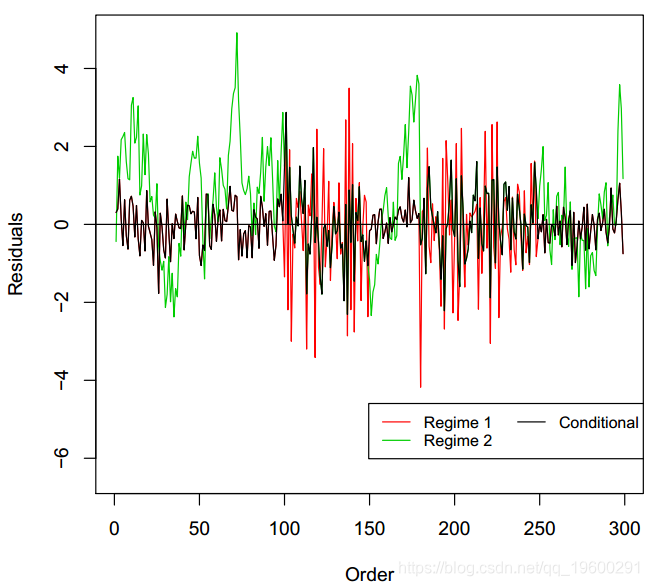
模型mod.mswm具有协方差x非常显着的状态，而在其他情况下，自相关变量也非常重要。两者的R平方均具有较高的值。最后，转移概率矩阵具有较高的值，这表明很难从接通状态更改为另一个状态。该模型可以完美地检测每个状态的周期。残差看起来像是白噪声，它们适合正态分布。而且，自相关消失了。
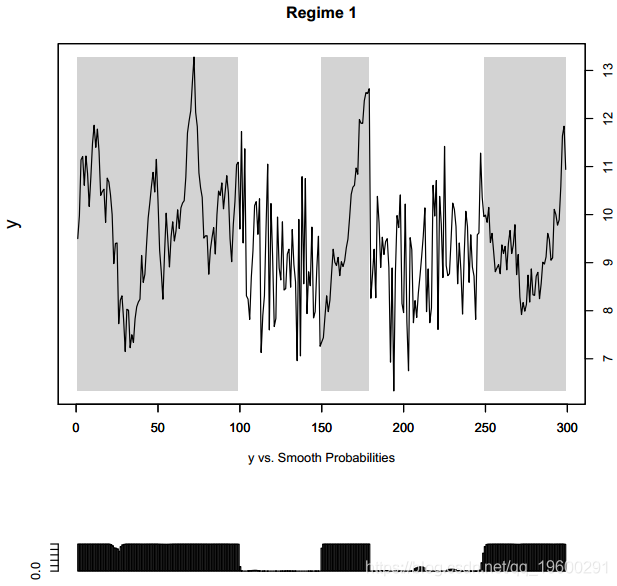
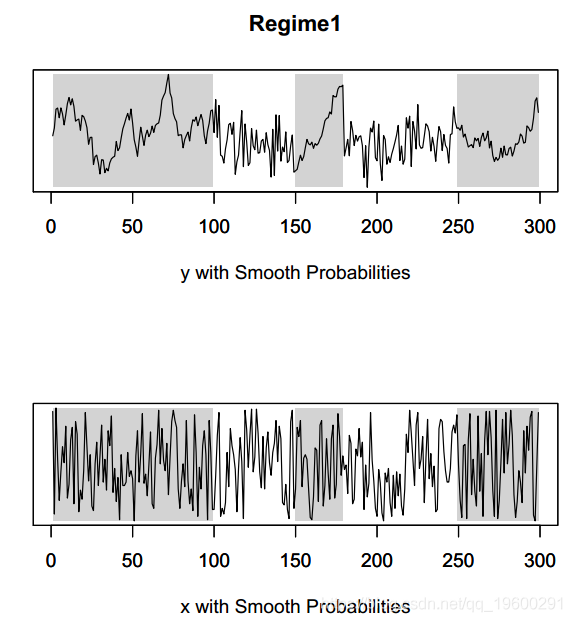
图形显示已完美检测到每个方案的周期。
> plot(mod.mswm,expl="x")
交通事故
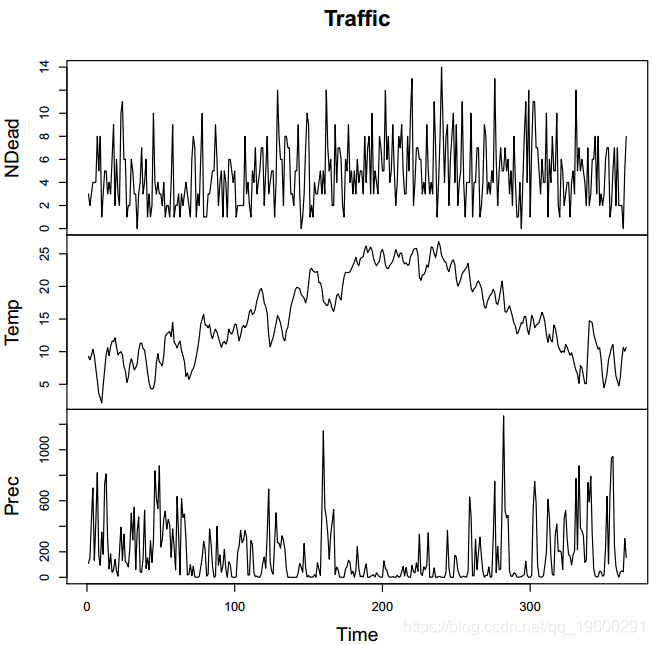
交通数据包含2010年西班牙交通事故的每日人数，平均每日温度和每日降水量。该数据的目的是研究死亡人数与气候条件之间的关系。由于在周末和工作日变量之间存在不同的行为，因此我们说明了在这种情况下使用广义马尔科夫转换模型的情况。
在此示例中，响应变量是计数变量。因此，我们拟合了泊松广义线性模型。
> summary(model)
Call:
glm(formula = NDead ~ Temp + Prec, family = "poisson", data = traffic)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1571 -1.0676 -0.2119 0.8080 3.0629
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.1638122 0.0808726 14.391 < 2e-16 ***
Temp 0.0225513 0.0041964 5.374 7.7e-08 ***
Prec 0.0002187 0.0001113 1.964 0.0495 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 597.03 on 364 degrees of freedom
Residual deviance: 567.94 on 362 degrees of freedom
AIC: 1755.9
Number of Fisher Scoring iterations: 5
下一步，使用拟合马尔可夫转换模型。为了适应广义马尔可夫转换模型，必须包含族参数，而且glm没有标准偏差参数，因此sw参数不包含其切换参数。
>
Markov Switching Model
AIC BIC logLik
1713.878 1772.676 -850.9388
Coefficients:
Regime 1
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 0.7649 0.1755 4.3584 1.31e-05 ***
Temp(S) 0.0288 0.0082 3.5122 0.0004444 ***
Prec(S) 0.0002 0.0002 1.0000 0.3173105
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Regime 2
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 1.5659 0.1576 9.9359 < 2e-16 ***
Temp(S) 0.0194 0.0080 2.4250 0.01531 *
Prec(S) 0.0004 0.0002 2.0000 0.04550 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Transition probabilities:
Regime 1 Regime 2
Regime 1 0.7287732 0.4913893
Regime 2 0.2712268 0.5086107两种状态都有显着的协变量，但降水协变量仅在这两种状态之一中是显着的。
Aproximate intervals for the coefficients. Level= 0.95
(Intercept):
Lower Estimation Upper
Regime 1 0.4208398 0.7648733 1.108907
Regime 2 1.2569375 1.5658582 1.874779
Temp:
Lower Estimation Upper
Regime 1 0.012728077 0.02884933 0.04497059
Regime 2 0.003708441 0.01939770 0.03508696
Prec:
Lower Estimation Upper
Regime 1 -1.832783e-04 0.0001846684 0.0005526152
Regime 2 -4.808567e-05 0.0004106061 0.0008692979 
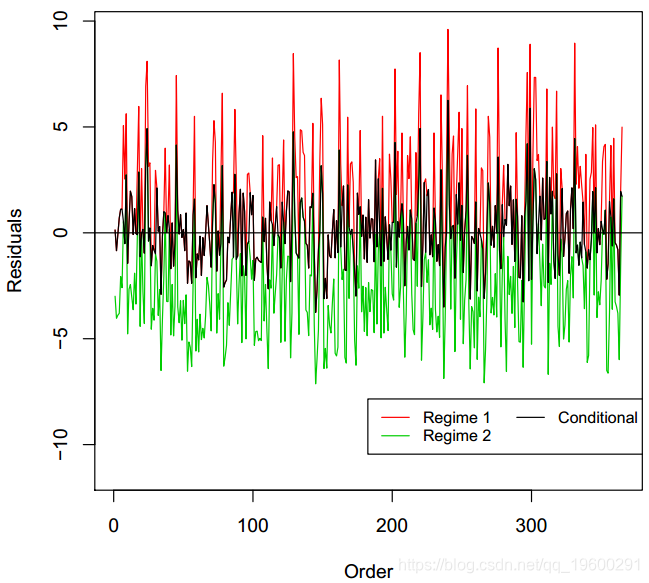
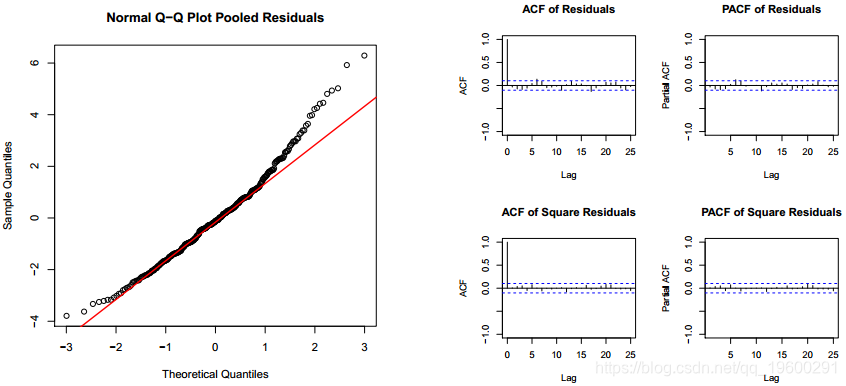
由于模型是通用线性模型的扩展，因此从类对象计算出图中的Pearson残差。该残差有白噪声的经典结构。残差不是自相关的，但它们与正态分布不太吻合。但是，Pearson残差的正态性不是广义线性模型验证的关键条件。
> plot(m1,which=2)
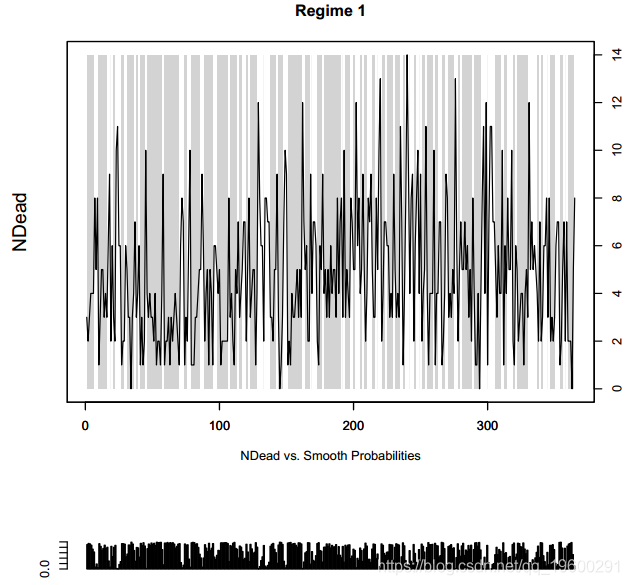
我们可以看到短时间内的状态分配，因为较大的状态基本上包含工作日。