原文链接: http://tecdat.cn/?p=8199
本文中我在R中构造一个简单的M / M / 1队列的离散事件模拟 。
模拟变量
像往常一样,我们从模拟及其检测所需的变量 开始。
接下来,我们需要编写R代码以对进入队列和从队列离开进行实际的M / M / 1模拟。
仿真循环
检测指标
在这里,我们 检测数据以形成一些众所周知的性能指标。
队列长度
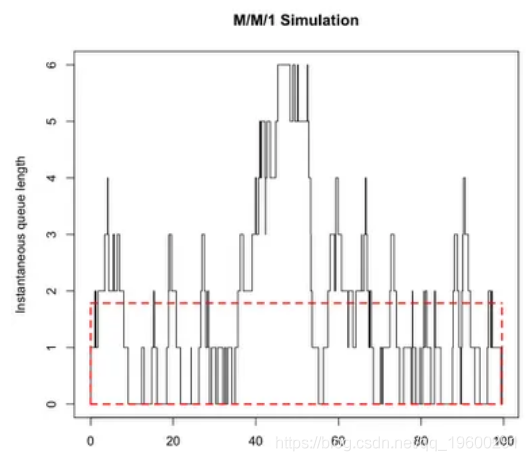
这是瞬时队列长度- 平均负载数据的曲线图。这就是排队波动的样子。
显示为红色虚线的框具有与阶梯曲线下方相同的面积。
PDQ模型
为了进行分析比较,我们还使用 PDQ-R模型。
是的,这几行代码与上面带工具的仿真代码等效,并且可以保证处于稳定状态。即使在R中运行PDQ本质上也是瞬时的。模拟将花费更长的时间,
结果
最后,我们可以将模拟的M / M / 1队列与相应的PDQ结果进行比较。像往常一样,最好将它们分解为输入和输出。
- 输入:
Tsim:1.00e + 05
Ta:1.3333,Ts:1.0000#次
Ar:0.7500,Sr:1.0000# - 输出:
Usim:0.7477,Updq:0.75
Xsim:0.7495,Xpdq:0.75
Rsim:4.0316,Rpdq:4.00
Qsim:3.0219,Qpdq:3.00
我们可以得出结论,仿真在指定的10 5个时间步长内达到了稳态。