本示例说明如何测量信号相似度。将回答以下问题：如何比较具有不同长度或不同采样率的信号？如何确定测量中是否存在信号或仅有噪声？有两个信号相关吗？如何测量两个信号之间的延迟？
比较具有不同采样率的信号
考虑一个音频信号数据库和一个模式匹配应用程序，您需要在其中识别正在播放的歌曲。数据通常以低采样率存储，以占用更少的内存。
figure
ax(1) = subplot(3,1,1);
plot((0:numel(T1)-1)/Fs1,T1,'k')
ylabel('Template 1')
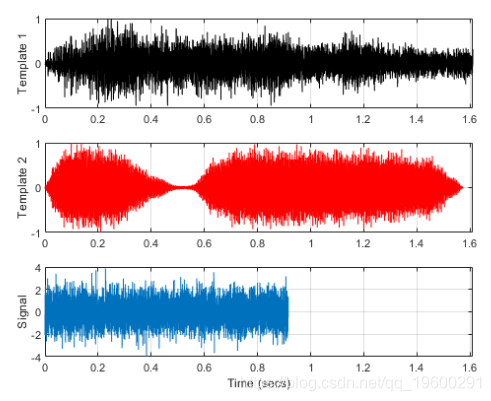
第一个和第二个子图显示了来自数据库的模板信号。第三个子图显示了我们要在数据库中搜索的信号。仅查看时间序列，信号似乎与两个模板都不匹配。仔细检查发现，信号实际上具有不同的长度和采样率。
[Fs1 Fs2 Fs]
ans = 1×3
4096 4096 8192不同的长度使您无法计算两个信号之间的差异，但是可以通过提取信号的公共部分来轻松解决。此外，并不总是必须使长度相等。
在测量中寻找信号
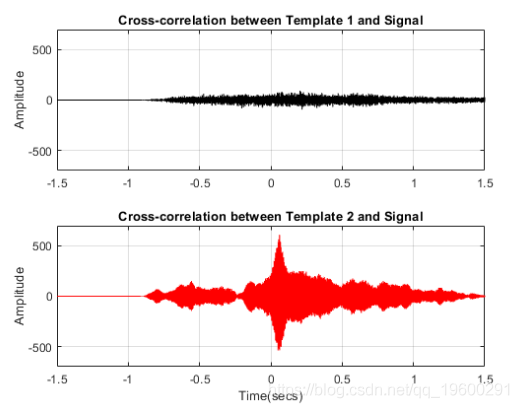
现在，我们可以使用xcorr函数将信号S与模板T1和T2互相关，以确定是否存在匹配项。
figure
ax(1) = subplot(2,1,1);
plot(lag1/Fs,C1,'k')
ylabel('Amplitude')
grid on
第一个子图表示信号与模板1的相关性较低，而第二个子图中的高峰值表示信号存在于第二个模板中。
互相关的峰值表示信号在61 ms之后开始存在于模板T2中。换句话说，信号T2使信号S超前499个采样，如SampleDiff所示。
测量信号之间的延迟并对齐它们
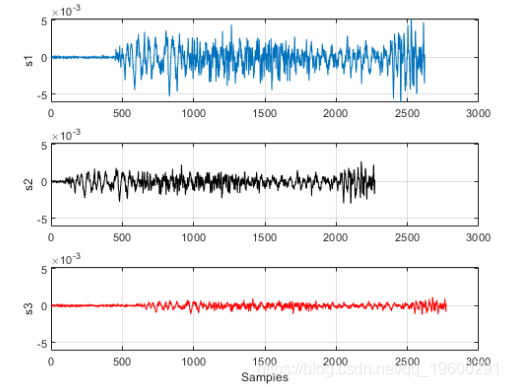
考虑一种情况，您正在从不同的传感器收集数据，记录桥两边的汽车引起的振动。分析信号时，可能需要对齐它们。假设您有3个传感器以相同的采样率工作，并且它们正在测量由同一事件引起的信号。
figure,
ax(1) = subplot(3,1,1);
plot(s1)
我们还可以查找两个信号之间的延迟。
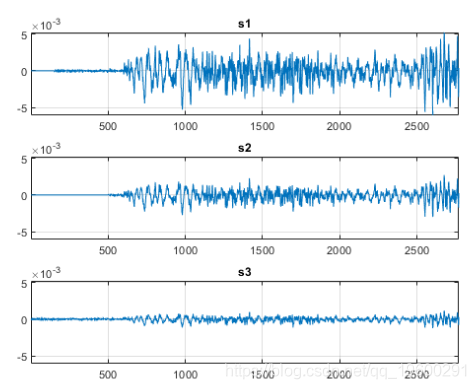
t21表示s2落后s1 350个样本，t31表示s3领先s1 150个样本。该信息现在可用于通过时移信号来对齐3个信号。我们还可以alignsignals直接使用该功能来对齐信号，这可以通过延迟最早的信号来对齐两个信号。
s1 = alignsignals(s1,s3);
s2 = alignsignals(s2,s3);
figure
ax(1) = subplot(3,1,1);
plot(s1)
grid on
title('s1')
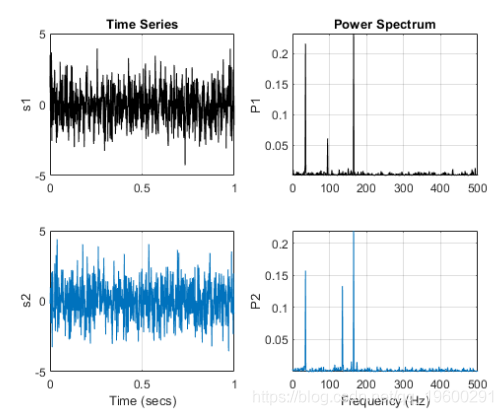
比较信号的频率
功率谱显示每个频率中存在的功率。频谱相干性识别信号之间的频域相关性。趋向于0的相干值表示相应的频率分量是不相关的，而趋向于1的值则表示相应的频率分量是相关的。
figure
t = (0:numel(sig1)-1)/Fs;
subplot(2,2,1)
plot(t,sig1,'k')
ylabel('s1')
grid on
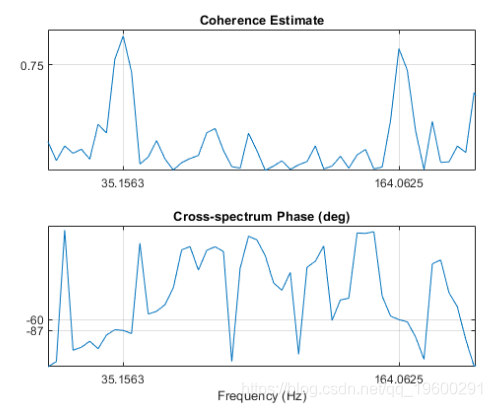
计算两个信号之间的频谱相干性。 确认sig1和sig2在35 Hz和165 Hz附近具有两个相关分量。在频谱相干性很高的频率中，可以使用互谱相位来估计相关分量之间的相对相位。
figure
subplot(2,1,1)
plot(f,Cxy)
title('Coherence Estimate')
grid on
35 Hz分量之间的相位滞后接近-90度，而165 Hz分量之间的相位滞后接近-60度。
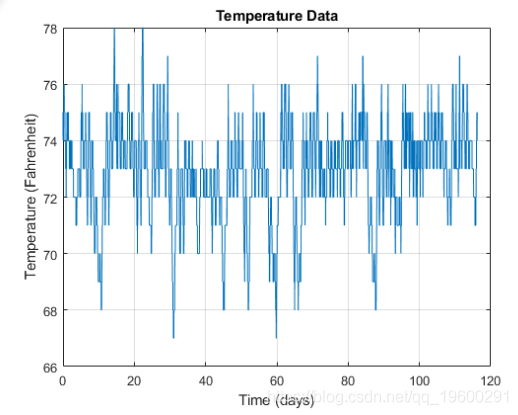
查找信号中的周期
冬季办公大楼中的一组温度测量值。每30分钟进行一次测量，持续约16.5周。
figure
plot(days,temp)
title('Temperature Data')
xlabel('Time (days)')
ylabel('Temperature (Fahrenheit)')
grid on
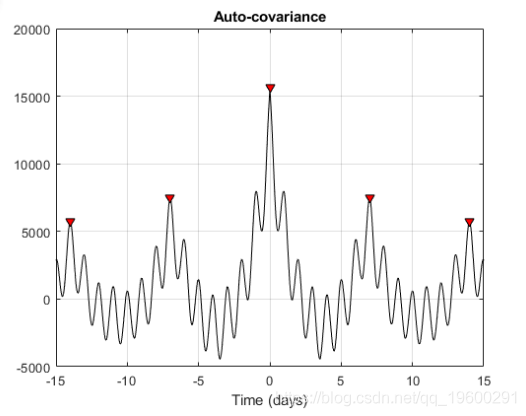
在计算互相关之前去除信号的均值。它返回交叉协方差。将最大滞后限制为信号的50％，以获得对互协方差的良好估计。
figure
plot(lag/(2*24),xc,'k',...
lag(df)/(2*24),xc(df),'kv','MarkerFaceColor','r')
grid on
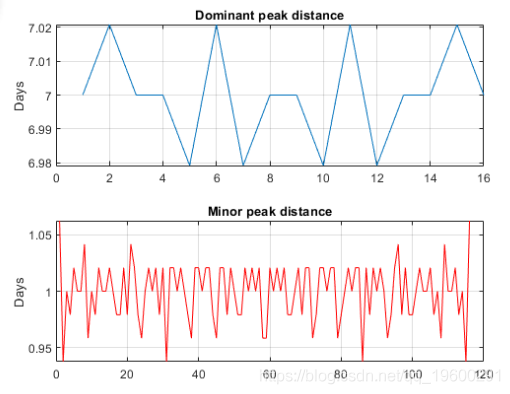
观察自协方差的主要和次要波动。主峰和次峰出现等距。要验证它们是否正确，请计算并绘制后续峰位置之间的差异。
cycle1 = diff(df)/(2*24);
subplot(2,1,1)
plot(cycle1)
ylabel('Days')
mean(cycle1)
ans = 7
mean(cycle2)
ans = 1.0000
次要峰表示每周7个循环，主要峰表示每周1个循环。鉴于数据来自7天日历上的温度受控建筑物，因此这是有道理的。第一个7天的周期表示建筑物温度有一个每周的循环行为，其中周末温度降低，而工作日则恢复正常。1天的循环行为表示每天都有循环行为-夜间温度较低，白天则升高。